5.2 Injections, Surjections, and Bijections
In this section we will define and explore several different properties that some functions have that provide useful information about the function.
Definition 5.2 A function \(f:A\rightarrow B\) is called an injection, or one-to-one, if no two elements of the domain map to the same element of the co-domain. Or equivalently, for elements \(a_1,a_2 \in A\), \[\left(f(a_1)=f(a_2)\right) \Rightarrow \left(a_1=a_2\right).\]
The primary benefit of a function being an injection is that for each element, \(b\), in the range of the function, there is a unique element, \(a\), in the domain of the function such that \(f(a)=b\). This provides the foundation for ‘undoing’ functions that we will explore further in the next section.
The simplest example of a function that is not one-to-one is given by a function from \(A=\{a,b\}\) to \(B=\{c\}\) represented by
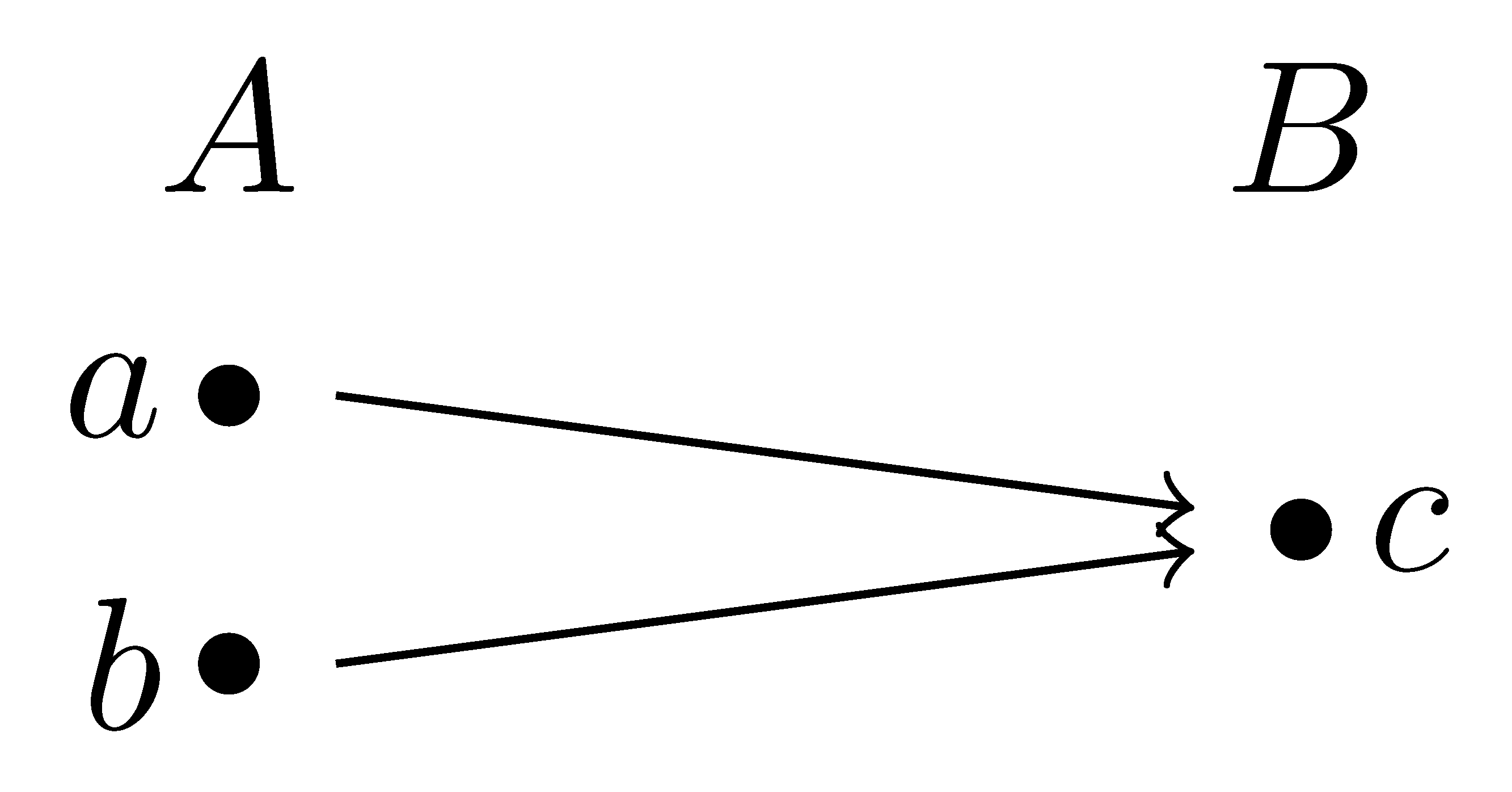
since \(f(a)=f(b)\), but \(a\neq b\).
We can also see that the function \(f(x)=|x|\) is not one-to-one because \(f(-x)=f(x)=|x|\) for all \(x\in \mathbb{R}\).
The function \[f(x)=\begin{cases} x & \mbox{if } x\neq 0 \\ 1 & \mbox{if } x=0 \end{cases}\] is not one-to-one since \(f(1)=f(0)\). If we sketch the graph of this function, we can see that this
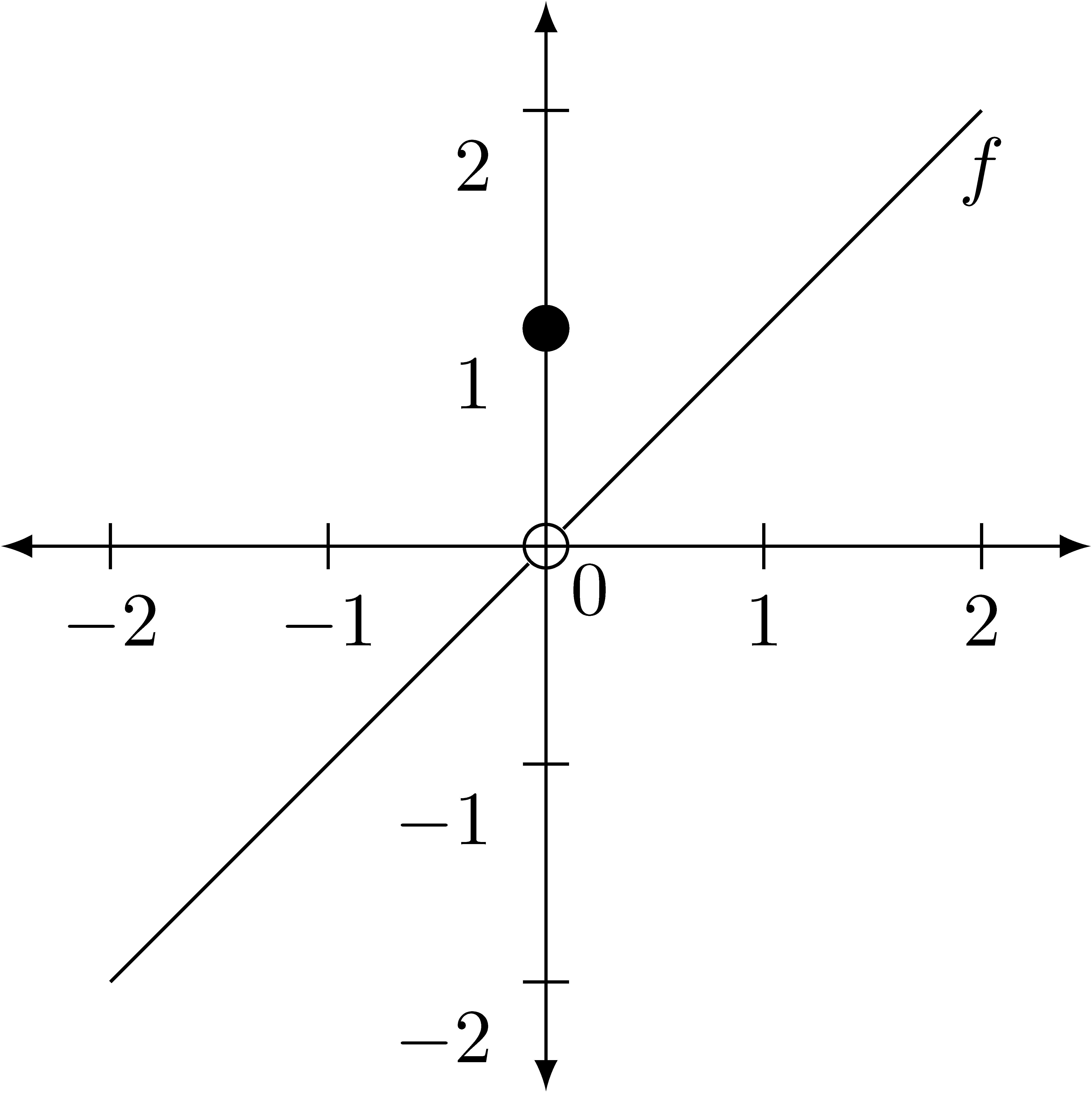
is true because if one draws a horizontal line at \(y=1\), it intersects the function at two places. This intersection at multiple places by a horizontal line is called the horizontal line test. So if a function does not pass the horizontal line test, then it is not one-to-one.
Sometimes a function cannot be graphed easily and we would like to prove that it is one-to-one. There is a fairly standard process for doing so using the one-to-one definition. In this process, we assume that \(a\) and \(b\) are in the domain of a function \(f:A\rightarrow B\) such that \(f(a)=f(b)\). Then using some logical arguments we prove that this implies that \(a=b\). To prove that a function is not one-to-one we only need to find one case of two distinct elements in the domain mapping to the same element in the co-domain.
Definition 5.3 A function \(f:A\rightarrow B\) is called a surjection, or onto, if every element of the co-domain is in the range of \(f\). Or equivalently, if for all \(b\in B\) there exists a \(a\in A\) such that \(f(a)=b\).
A primary consideration in a function being a surjection is to know that every element in the co-domain is ‘hit’ by an element in the domain. It is often more important to fully describe the range of the function, rather than if a function is a surjection, since any function is a surjection when the co-domain of the function is replaced by the range of the function in the definition of the function. For instance, \(f:\mathbb{R}\rightarrow \mathbb{R}\) defined by \(f(x)=x^2\) is not a surjection, since negative numbers cannot be in the range. But \(f:\mathbb{R}\rightarrow \mathbb{R}^+\) (where \(\mathbb{R}^+=[0,\infty)\)) defined by \(f(x)=x^2\) is a surjection.
The basic example of a function that is not a surjection is given by a function \(f:A=\{a\} \rightarrow B=\{b,c\}\) represented by

Note: This function is one-to-one, but not onto. While the example of a function that maps from two elements to one element above is onto, but not one-to-one.
Definition 5.4 A function \(f:A\rightarrow B\) is called a bijection, or one-to-one and onto, if it is both an injection and a surjection.
One of the results of a function being a bijection is that there is a perfect correspondence between elements of the domain and elements of the co-domain that we will explore further in the next two sections.
5.2.1 Exercises
For each of the following functions, determine if it is an injection, a surjection, and/or a bijection.
\(f:\mathbb{R}\rightarrow \mathbb{R}\) defined by \(f(x)=x\).
\(f:\mathbb{R} \rightarrow [0,\infty)\) defined by \(f(x)=|x|\).
\(f:[0,\infty) \rightarrow \mathbb{R}\) defined by \(f(x)=x^2\).
\(f:\mathbb{R}\setminus \{0\} \rightarrow \mathbb{R}\setminus \{0\}\) defined by \(f(x)=\frac{1}{x}\).
\(f:\mathbb{N} \rightarrow \mathbb{R}\) defined by \[f(x)=\frac{x}{1+x^2}.\]