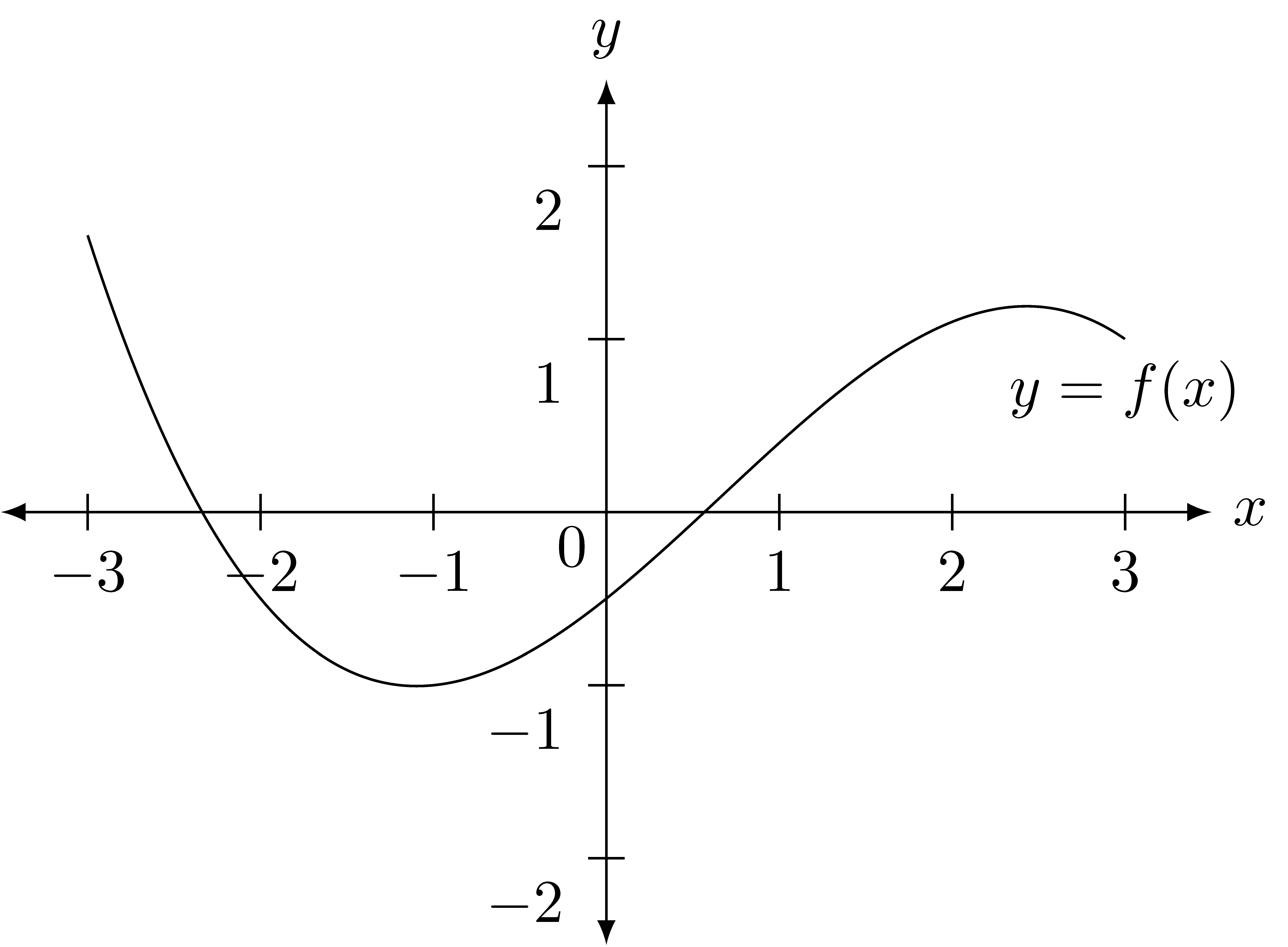9.2 Transformations of Functions
When modeling using a function, it is usually helpful to transform the function by a combination of translations, dilations, and reflections in order to have the function fit the situation being modeled.
As an example, we will look at a model of the number of hours of daylight in London, England for each day during 2020. We notice that the hours of daylight are periodic and that they resemble a trigonometric function. This function has a period of \(365.25\) days and we calculate the average length of daylight to be \(12\) hours and \(14\) minutes, which first occurs on the \(81\)st day of the year. So we can model the situation with the function \[f(x)= \left( \frac{\mbox{max hours of daylight} - \mbox{min hours of daylight}}{2}\right) \cdot \sin \left(\frac{2\pi}{365.25} \left(x-81\right)\right) + 12:14\] As we can see in below, this function models the situation fairly well.

Figure 9.3: Hours of Daylight for London, 2020
We will study the family of functions generated from a parent function using these transformations throughout the rest of the chapter, using the function \(f\) given by the graph in Figure 9.4 as an example.
Figure 9.4: Tranformations: Base Function
9.2.1 Horizontal Translations
Given a function \(f\) and a constant \(h\), a new function \(g(x)=f(x-h)\) is a horizontal translation of the function \(f\). If \(h\) is positive, then \(y=g(x)\) is a translation of \(y=f(x)\) by \(h\) units to the right. If \(h\) is negative, it is a translation to the left.
Figure 9.5: Tranformations: Horizontal Translation
Related Content Standards
- (HSF.BF.3) Identify the effect on the graph of replacing \(f(x)\) by \(f(x) + k\), \(k f(x)\), \(f(kx)\), and \(f(x + k)\) for specific values of \(k\) (both positive and negative); find the value of \(k\) given the graphs. Experiment with cases and illustrate an explanation of the effects on the graph using technology. Include recognizing even and odd functions from their graphs and algebraic expressions for them.
9.2.2 Vertical Translations
Given a function \(f\) and a constant \(k\), a new function \(g(x)=f(x)+k\) is a vertical translation of the function \(f\). If \(k\) is positive, then \(y=g(x)\) is a translation of \(y=f(x)\) by \(k\) units up. If \(k\) is negative, it is a translation down.
Figure 9.6: Tranformations: Vertical Translation
9.2.3 Horizontal Dilations
In addition to the translations, we can dilate the function away from and closer to the vertical axis. Given a function \(f\) and a constant \(b>0\), a new function \(g(x)=f(bx)\) is a horizontal dilation by a factor of \(b\). If \(b>1\), the new function is a compression towards the vertical axis by a factor of \(b\). If \(0<b<1\), the new function is a dilation away from the vertical axis by a factor of \(\frac{1}{b}\).
Figure 9.7: Tranformations: Horizontal Dilation
9.2.4 Vertical Dilations
Similarly to the horizontal dilations, multiplying the output of a function by a positive constant dilates the function vertically. Given a function \(f\) and a constant \(a>0\), the function \(g(x)=a f(x)\) is a dilation towards the horizontal axis if \(0<a<1\) and away from the horizontal axis if \(a>1\).
Figure 9.8: Tranformations: Vertical Dilation
9.2.5 Reflections
We are also able to reflect the graph of a function over the horizontal axis by changing the sign of the output of the function. So \(g(x)=-f(x)\) is a vertical reflection of \(f\) about the horizontal axis.
Figure 9.9: Tranformations: Vertical Reflection
By changing the sign of the variable in the domain, we can also reflect a function about the vertical axis so that the graph of \(g(x)=f(-x)\) is a horizontal reflection of the graph of \(f\) about the vertical axis.
Figure 9.10: Tranformations: Horizontal Reflection
9.2.6 Families of Functions
One can combine all of these transformations together in order to generate a family of functions related to the original function \(f\), \[g(x)= a\cdot f(b(x-h))+k.\] In each of the next few sections we will study the family of functions related to the parent functions of \(f(x)=x\), \(f(x)=e^x\), \(f(x)=\frac{1}{x}\), \(f(x)=x^2\), and the basic trigonometric functions, along with each of their inverse functions when those functions exist.