13.5 Reflections
Continuing our illustrations of isometries using a piece of paper to represent the plane, a reflection corresponds to flipping the paper over while keeping one line of the paper fixed. For example, holding two opposite corners of the paper still while flipping over the diagonal line.
13.5.1 Synthetic Plane
Theorem 13.15 Given a line \(\overleftrightarrow{AB}\) and a point \(C\) not on \(\overleftrightarrow{AB}\), there exists a unique point \(C'\) such that \(\overline{CC'}\) is perpendicular to \(\overleftrightarrow{AB}\) and \(\overleftrightarrow{AB}\) intersects \(\overline{CC'}\) at its midpoint. We will call the point \(C'\) the reflection of \(C\) about \(\overleftrightarrow{AB}\).
As in the figure below, for a given line \(\overleftrightarrow{AB}\) and a point \(C\) not on the line we can find points \(D\) and \(E\) on \(\overleftrightarrow{AB}\) that are equidistant from \(C\). We then construct the circles centered at \(D\) and \(E\) through the point \(C\). These circles then intersect at another point, \(C'\), that is the reflection of \(C\) about \(\overleftrightarrow{AB}\).
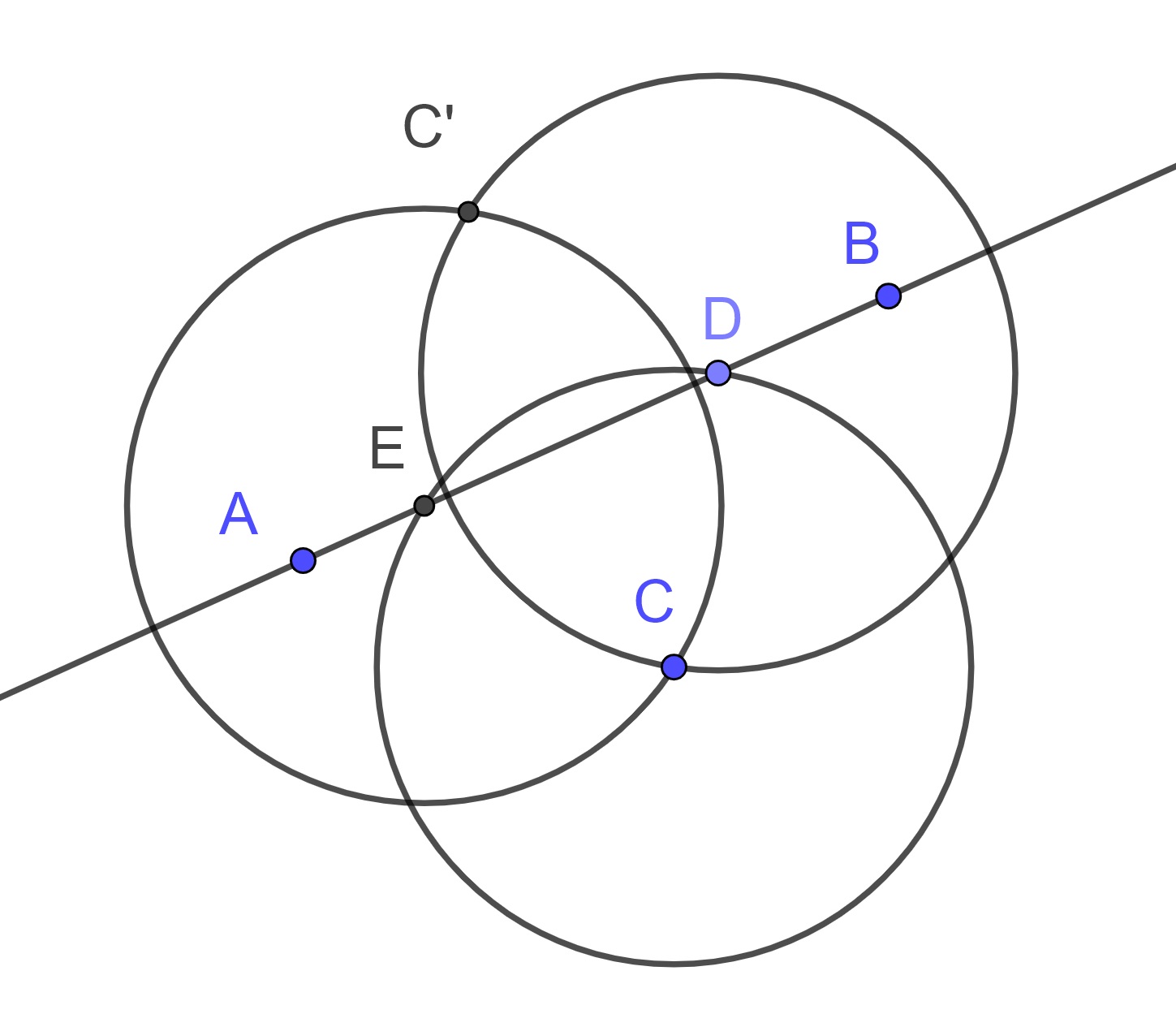
Definition 13.17 Given a line \(\overleftrightarrow{AB}\) we define the reflection about \(\overleftrightarrow{AB}\), \(r_{\overleftrightarrow{AB}}\), for a point \(C\) as \(C\) if \(C\in \overleftrightarrow{AB}\) and as its reflection about \(\overleftrightarrow{AB}\) otherwise.
13.5.2 Complex Plane
We see that the function \(f(z)=\overline{z}\) is a reflection about the real axis. In order to define a reflection about a generic line we can first use translations and rotations to map that line to the real axis, perform the reflection, and then transform the real axis back to the original line. So if \(l\) is a line, we can choose a point \(c\) on the line and we can let \(\theta\) be the angle that the line makes with the horizontal axis. This point and angle then define the line, \[l = \left\{ z\in \mathbb{C} \: \vert \: z=c+re^{i\theta} \mbox{ for some } r\in \mathbb{R} \right\}.\] So by translating the plane so that \(c\) maps to \(0\), \(T_{-c}\); rotating the plane so that the image of the line maps to the real axis, \(R_{(0,-\theta)}\); reflecting about the real axis, \(r_{\mbox{Im}(z)=0}\); rotating the real axis back to a line with angle \(\theta\) with the horizontal, \(R_{(0,\theta)}\); and finally a translation that maps \(0\) back to \(c\), \(T_{c}\), we have the reflection about the line \(l\), \[r_l (z) = T_c \circ R_{(0,\theta)} \circ r_{\mbox{Im}(z)=0} \circ R_{(0,-\theta)} \circ T_{-c} (z) = e^{i(2\theta )} \: \overline{(z-c)} +c.\]
Definition 13.18 Let \(l\) be a line through a point \(c\) making an angle \(\theta\) with the real axis. Then we define \[r_{(c,\theta)}(z)= e^{i(2\theta )} \: \overline{(z-c)} +c\] and see that this function is a reflection about the line \(l\).
We can see from the expression for the reflections that they are of the form \(f(z)=a \overline{z}+b\) for complex numbers \(a\) and \(b\), with \(|a|=1\). However, we see in the following theorem that not all functions of this form are reflections.
Theorem 13.16 Let \(f(z)=a\overline{z} + b\) be a function such that \(|a|=1\). Then \(f\) is a reflection if and only if \(a\overline{b}+b=0\).
Proof. If we first assume that \(f\) is a reflection, then there is a point \(c\) and an angle \(\theta\) such that \[f(z) = e^{i(2\theta)} \: \overline{(z-c)} +c.\] So \(f(z)=a\overline{z} +b\) for \(a=e^{i(2\theta)}\), so that \(|a|=1\), and \(b= c-e^{i(2\theta)} \: \overline{c}\). Then \[a\overline{b} + b = e^{i(2\theta)} \cdot \left(\overline{c}-e^{-i(2\theta)} \: c\right) + c-e^{i(2\theta)}\: \overline{c}=0.\]
If we let \(f(z)=a\overline{z}+b\) for some \(a,b\in \mathbb{C}\) such that \(|a|=1\) and \(a\overline{b}+b=0\), there exists an angle \(\theta\) such that \(a= e^{i(2\theta)}\). We also know that \[a\overline{z}+b= a\overline{z} + \frac{b}{2}-\frac{a\overline{b}}{2} + \frac{b}{2} + \frac{a\overline{b}}{2} = a \overline{z} - a \frac{\overline{b}}{2} + \frac{b}{2} + \frac{a\overline{b}+b}{2} = a \overline{\left(z-\frac{b}{2}\right)} + \frac{b}{2} + \frac{a\overline{b}+b}{2}.\] Since \(a\overline{b}+b=0\), we see that \[f(z)=e^{i(2\theta)}\; \overline{\left(z-\frac{b}{2}\right)} + \frac{b}{2}\] and so \(f\) is a reflection about the line through \(\frac{b}{2}\) making an angle \(\theta\) with the real axis.
13.5.3 Vector Space and Cartesian Plane
As we did with rotations, we will use the information from the Complex Plane representation to determine the representation of reflections in the Vector Space and Cartesian Plane representations.
Reflections over the horizontal axis are described by \(\langle x,y \rangle \mapsto \langle x,-y\rangle\). So using matrices, this reflection can be represented by the matrix \[r_{y=0} = \begin{pmatrix} 1 & 0 \\ 0 & -1 \end{pmatrix}.\] If we combine this matrix with the transformations of rotation and translation we see that the reflection about a line, \(l\), through the point \((h,k)\) making an angle \(\theta\) with the horizontal is described as \[\begin{align*} r_l (\langle x,y\rangle ) &= \begin{pmatrix} \cos(2\theta) & -\sin(2\theta) \\ \sin(2\theta) & \cos(2\theta) \end{pmatrix} \begin{pmatrix} 1 & 0 \\ 0 & -1 \end{pmatrix} \begin{pmatrix} x-h \\ y-k \end{pmatrix} + \begin{pmatrix} h \\ k \end{pmatrix} \\ &= \begin{pmatrix} (x-h) \cos(2\theta) + (y-k)\sin(2\theta) +h \\ (x-h) \sin(2\theta) - (y-k)\cos(2\theta) +k \end{pmatrix} .\end{align*}\]
So the Cartesian Plane representation of a reflection about a line \(l\) through a point \((h,k)\) making an angle \(\theta\) with the horizontal is given by \[r_{l} (x,y) = \left( (x-h) \cos(2\theta) + (y-k)\sin(2\theta) +h, (x-h) \sin(2\theta) - (y-k)\cos(2\theta) +k \right) .\] For the special case of a reflection about the vertical axis, we let \((h,k)=(0,0)\) and \(\theta=\frac{\pi}{2}\) to see that \(r_{x=0} (x,y) = (-x,y)\). For the reflection about the line \(y=x\), we can use the points \((0,0)\) and the angle \(\frac{\pi}{4}\) to see that \(r_{y=x}(x,y) = (y,x)\).
13.5.4 Compositions
If \(r_1 (z) = e^{i(2\theta_1)} \: \overline{(z-c_1)} + c_1\) and \(r_2 (z) = e^{i(2\theta_2)} \: \overline{(z-c_2)} + c_2\) are two generic reflections, we see that the composition of the two reflections is \[\begin{align*} r_1 \circ r_2 (z) & = e^{i (2\theta_1)} \: \overline{ \left( e^{i(2\theta_2)} \: \overline{(z-c_2)} + c_2-c_1 \right)} + c_1 \\ & = e^{i (2\theta_1)} \: \left( e^{-i(2\theta_2)} (z-c_2) + \overline{c_2-c_1} \right) + c_1 \\ & = e^{i 2(\theta_1-\theta_2)} z + c_3\\ \end{align*}\] where \(c_3 = -e^{i2(\theta_1-\theta_2)}c_2 + e^{i(2\theta_1)} \: \overline{\left(c_2-c_1\right)} +c_1\).
If the two reflections are the same, we see that the composition generates the identity function.
Theorem 13.17 If \(m\) is a line in the plane with \(r_m\) denoting the reflection about \(m\), then \(r_m^{-1}=r_m\). In other words, each reflection is its own inverse.
If the two lines are distinct, \(r_1 \circ r_2\) is a transformation that is a translation if \(e^{i 2(\theta_1-\theta_2)}=1\), and a rotation otherwise.
When the composition is a translation, the difference between the angles of the two lines of reflection is a multiple of \(\pi\) and so the two lines are parallel. So we can assume that \(\theta_1=\theta_2\) and so \[\begin{align*} r_1 \circ r_2 (z) & = z-c_2 +e^{i(2\theta_1)} \overline{c_2} - e^{i(2\theta_1)} \overline{c_1} + c_1 \\ & = z+ e^{i\theta_1} \left( e^{i\theta_1} \overline{c_2} - e^{-i\theta_1} c_2 + e^{-i\theta_1}c_1 - e^{i\theta_1} \overline{c_1} \right) \\ & = z + e^{i \theta_1} \left( e^{i \theta_1} \overline{(c_2-c_1)} - e^{-i\theta_1} (c_2-c_1)\right) \\ & = z + e^{i\theta_1} \left( 2i \mbox{Im} \left( e^{i \theta_1} \overline{(c_2-c_1)} \right) \right) \\ & = z + e^{i (\theta_1+\frac{\pi}{2})} 2 \mbox{Im} \left( e^{i \theta_1} \overline{(c_2-c_1)} \right) , \end{align*}\] which is a translation in the direction perpendicular to the two lines, with a magnitude of twice the distance between the two lines, and in the direction from the line of reflection of \(r_2\) towards the line of reflection of \(r_1\).
When the composition is a rotation, we know that the lines are not parallel and so they intersect. Without any loss of generality we can rewrite the equations of the two reflections through this point \(c\) as \[r_1(z) = e^{i (2\theta_1)} \: \overline{(z-c)} +c \quad \mbox{and} \quad r_2(z) = e^{i (2\theta_2)} \: \overline{(z-c)} + c\] and the composition as \[r_1 \circ r_2 (z) = e^{i2(\theta_1-\theta_2)} \: \overline{(z-c)} +c.\] So we see that the center of rotation is the intersection point of the two lines. The angle of rotation is then twice the angle from the line of reflection for \(r_2\) towards the line of reflection of \(r_1\).
We combine all of this information into the following theorem.
Theorem 13.18 (Two-Reflection Theorem) Let \(m\) and \(n\) be two distinct lines in the plane and let \(r_m\) and \(r_n\) be the reflections about the lines.
If \(m\) and \(n\) intersect at a point \(c\), then \(r_n\circ r_m\) is a rotation centered at \(c\) with angle of rotation double the angle from \(m\) to \(n\). Furthermore, \(r_m \circ r_n\) is a rotation centered at \(c\) with angle of rotation double the angle from \(n\) to \(m\).
If \(m\) and \(n\) are parallel lines, \(r_n\circ r_m\) is a translation that is perpendicular to the two lines with a magnitude twice the distance between the lines in the direction from \(m\) to \(n\). Similarly, \(r_m \circ r_n\) is a translation perpendicular to the lines with magnitude of twice the distance from \(n\) to \(m\).
13.5.5 Exercises
Use properties of triangles and quadrilaterals to show that the reflections defined on the synthetic plane are isometries. (Make sure to include all possible cases of the relationships between the two points and the line of reflection.)
Let \(r\) be the reflection across the line \(y=\sqrt{3}x\).
- Write an algebraic representation for the reflection from each of the four Cartesian, Vector, and Complex perspectives.
- Find the image of the circle \(C=\left\{ (x,y)\in \mathbb{R}^2 \: \vert \: (x-2)^2+(y+3)^2 =9\right\}\) under this reflection.
- Let \(A=(1,2)\), \(B=(-2,3)\) and \(C=(0,0)\). Find the image of the triangle \(\triangle ABC\) under this reflection.
For the set of reflections, identify whether each the properties of abelian groups hold. For each property, prove it holds or identify an appropriate argument or counter-example as to why it does not.
- closure
- identity
- inverse
- commutativity