11.2 Decomposing and Composing
A key mathematical way of thinking is the ability to work with mathematical structures to decompose and recompose mathematical objects in multiple ways in order to better understand properties of the objects and become proficient in related mathematical computation. In early elementary grades, students decompose natural numbers into different sums of numbers in order to improve computational proficiency. This is particularly important in student understanding and use of the base 10 number system when asked to rewrite expressions like \(14 \times 32\) as \[(10+4)\times (30 +2) = (10 \times 30)+(4\times 30)+(10\times 2)+(4 \times 2).\]
Similarly we are able to better understand geometric shapes by decomposing the shape into shapes that we already understand, such as rectangles or rectangular prisms. We then use the additive properties of the units of measurement to better understand these new objects.
Related Content Standards
(3.MD.7) Relate area to the operations of multiplication and addition.
- Recognize area as additive. Find areas of rectilinear figures by decomposing them into non-overlapping rectangles and adding the areas of the non-overlapping parts, applying this technique to solve real world problems.
(4.MD.7) Recognize angle measure as additive. When an angle is decomposed into non-overlapping parts, the angle measure of the whole is the sum of the angle measures of the parts. Solve addition and subtraction problems to find unknown angles on a diagram in real world and mathematical problems, e.g., by using an equation with a symbol for the unknown angle measure
(5.MD.5) Relate volume to the operations of multiplication and addition and solve real world and mathematical problems involving volume.
- Recognize volume as additive. Find volumes of solid figures composed of two non-overlapping right rectangular prisms by adding the volumes of the non-overlapping parts, applying this technique to solve real world problems.
11.2.1 Area
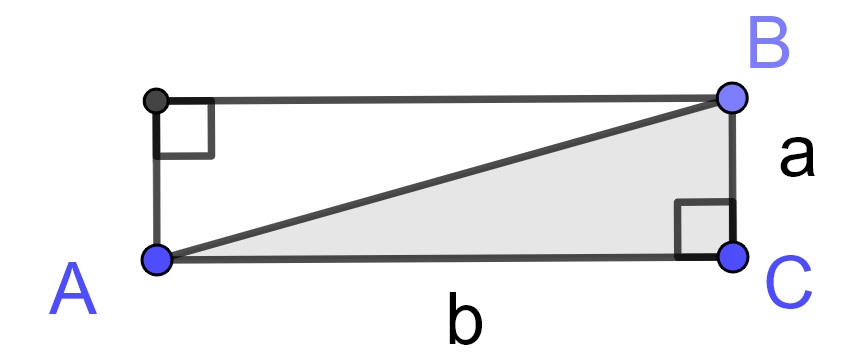
In the prior section we saw that the area of a rectangle can be found by multiplying the lengths of the two sides, \(A= l \times w\). We can use this to find a similar expression for the area of a right triangle. If we start with a right triangle \(\triangle ABC\) we can create a rectangle by joining to it a copy of itself. We then see that the area of a right triangle is equal to half of the product of the lengths of the two legs of right triangle.
If we have a triangle \(\triangle ABC\) that is not a right triangle, we can create an altitude from \(C\) to the opposite side of the triangle.
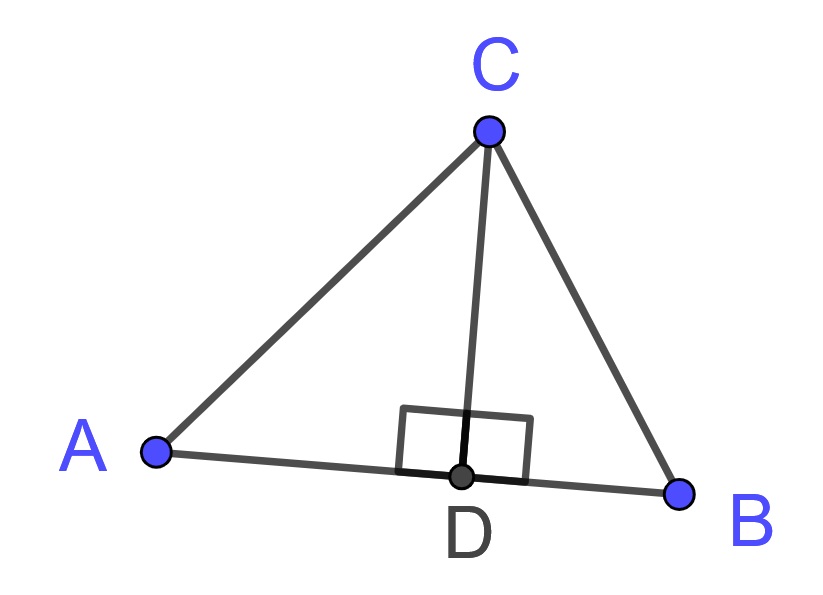
If the altitude is inside of the triangle we see that the original triangle is composed of two right triangles and we can derive that the area of the triangle equals half the product of the length of the altitude and the length the opposite side.
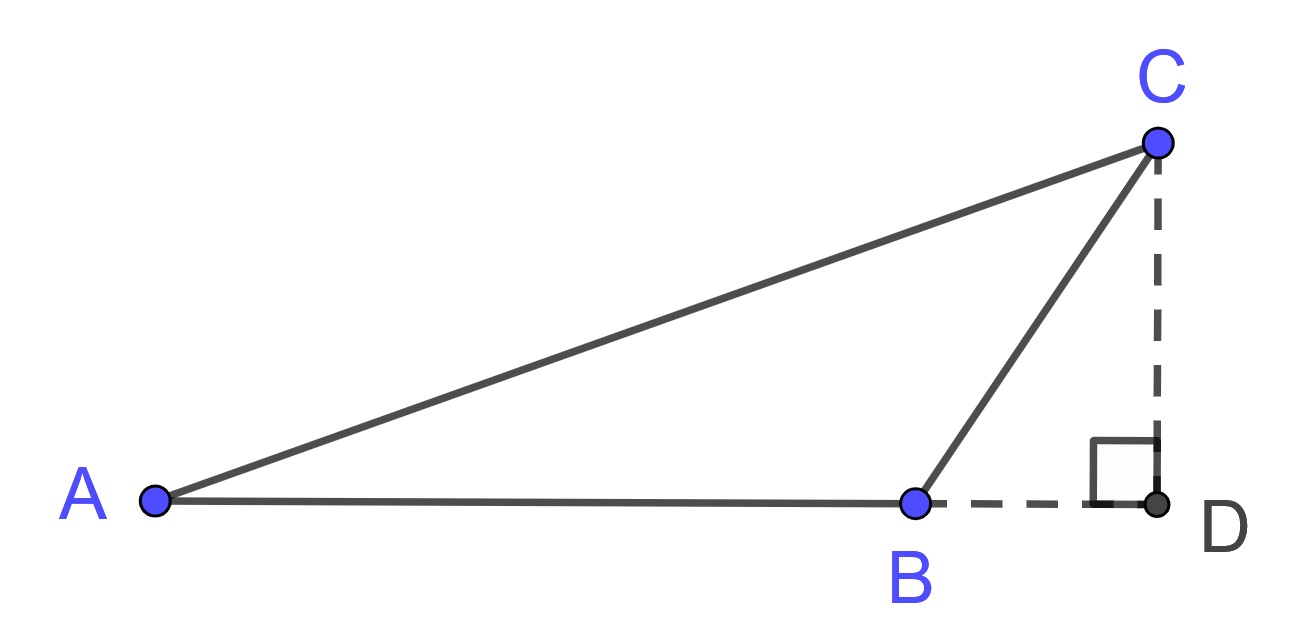
If the altitude is outside of the triangle we can see that the area of the original triangle equals the area of the right triangle \(\triangle ADC\) minus the area of the right triangle \(\triangle BDC\) giving the area as half the length of the altitude times the length of the opposite side of the triangle.
So for any triangle we have that the area is half the product of the side of the triangle and the height of the triangle from that side, \(A = \frac{1}{2} b \cdot h\).
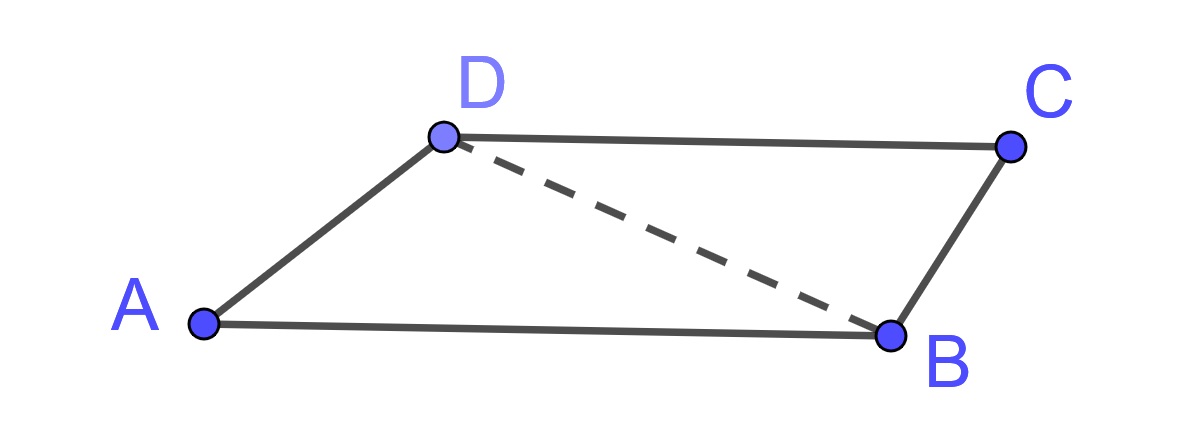
We can now use these areas of rectangles and triangles to find the areas of other two-dimensional objects. If \(ABCD\) is a parallelogram, we can divide the quadrilateral into two congruent triangles \(\triangle ABD\) and \(\triangle CDB\). Each of the triangles has an area of half the product of the length of one set of parallel sides and the length of the distance between those sides. So the area of the parallelogram is given by the product of the length of either set of parallel sides and the distance between those sides.

If \(ABCD\) is a trapezoid with sides \(AB\) and \(CD\) being parallel we can sketch the diagonal \(BD\) and see that the area of the quadrilateral is given by \[ \frac{1}{2} b_1 \cdot h + \frac{1}{2} b_2 \cdot h = \frac{1}{2} (b_1+b_2)\cdot h\] where \(b_1\) and \(b_2\) are the lengths of the two parallel sides and \(h\) is the distance between those sides.
Related Content Standards
- (6.G.1) Find the area of right triangles, other triangles, special quadrilaterals, and polygons by composing into rectangles or decomposing into triangles and other shapes; apply these techniques in the context of solving real-world and mathematical problems.
The constant ratio between the circumference and diameter of a circle, labeled as \(\pi\), allows us to generate formulas for the circumference in terms of both the diameter and radius of a circle, \(C=\pi d = 2 \pi r\). In order to understand the area of the circle we can divide the circle up into an even number of wedges of equal size. We can then rearrange the wedges as in the figure below.
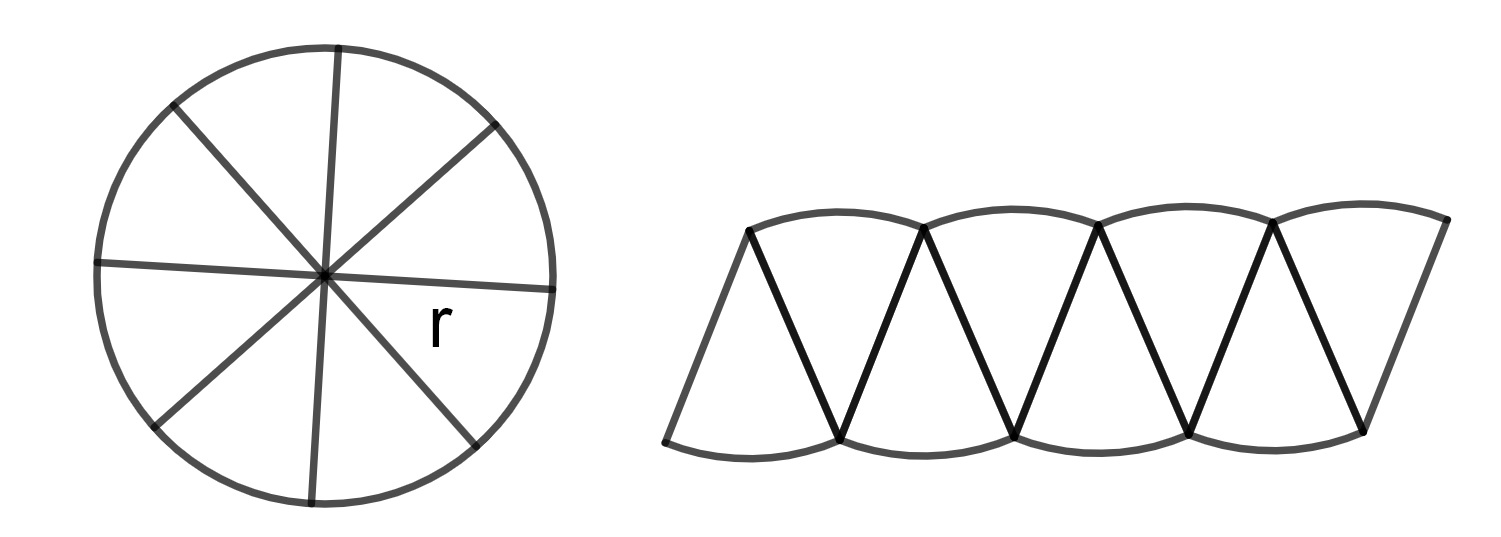
Then we see that as the number of wedges increase, the figure gets closer to a rectangle whose height equals the radius and the length of one of the other sides is half the circumference of the circle. Using an informal limiting argument, we can then see that the area of the circle is given by \[A = r \cdot \frac{1}{2} C = r \cdot \frac{1}{2} (2\pi r) = \pi r^2.\]
Related Content Standards
- (7.G.4) Know the formulas for the area and circumference of a circle and use them to solve problems; give an informal derivation of the relationship between the circumference and area of a circle.
11.2.2 Volume
We can follow the same lines of reasoning of decomposing and composing to determine the volumes of three dimensional figures. Archimedes used such ideas in the 3rd century BC with Bonaventure Cavalieri building on these ideas in the mid-1600’s.
Theorem 11.1 (Cavalieri's Principle) Suppose two regions in three-space (solids) are included between two parallel planes. If every plane parallel to these two planes intersects both regions in cross-sections of equal area, then the two regions have equal volumes.
These ideas are based on slicing the solid into infinitesimal slices and then adding up the volume of these slices. In the special case where the solid is a prism or cylinder each cross-section has an equal area. So Cavlieri’s prinicple implies that the volume of prisms or cylinders equals the area of each cross-section times the distance between the two parallel plane, \(V= A \cdot h\).
Volume of Cones and Pyramids (using limits)
In order to find the volume of a cone or pyramid whose height is \(d\), we let \(A(h)\) be the area of the cross-section \(h\) units from the base of the solid. Since the solid is a cone or pyramid, the area at each cross-section is proportional to the distance from the base relative to the height, \[A(h) = \left( 1 - \frac{h}{d}\right)^2 \cdot A(0),\] for \(0\leq h \leq d\).
We can now use the method of exhaustion of the ancient Greeks, as a precursor to calculus, to give an informal argument for the volume of the solid. We know that the solid has a volume less than the volume of the corresponding prism or cylinder, \(d \cdot A(0)\). We can get a better estimate for the solid by approximating it by multiple cylinders. If we use 4 cylinders to approximate the volume, we see that the sum of these four volumes is given by \[\frac{d}{4} \cdot A(0) + \frac{d}{4} \cdot A\left(\frac{d}{4}\right) + \frac{d}{4} \cdot A\left(\frac{2d}{4}\right) + \frac{d}{4} \cdot A\left(\frac{3d}{4}\right).\] This can be simplified to \[\frac{d}{4} \left( 1+\left(1-\frac{1}{4}\right)^2 + \left(1-\frac{2}{4}\right)^2 + \left(1-\frac{3}{4}\right)^2 \right) \cdot A(0)\] \[= \frac{d}{4} \cdot \left( \left(\frac{1}{4}\right)^2 + \left(\frac{2}{4}\right)^2 + \left(\frac{3}{4}\right)^2+1\right) \cdot A(0).\] So the area of the solid is approximated by \(\frac{30}{64} \cdot d \cdot A(0)\) when using 4 prisms. If we extend this to a larger number of divisions we will use information about the sum of the first \(n\) squares, \[P_n = \frac{n(n+1)(2n+1)}{6}.\] So if we approximate the solid by \(n\) prisms we have the volume as \[V \approx \frac{1}{n} \left(\sum_{i=1}^n \left( \frac{i}{n}\right)^2 \right) \cdot d \cdot A(0) = \frac{n(n+1)(2n+1)}{6n^3} \cdot d \cdot A(0).\] So, as the number of prisms increases, the volume approximation of the cone or pyramid approaches the true volume, \[V=\frac{1}{3} \cdot d \cdot A(0).\]
One can then use similar slicing arguments to show that the volume of a sphere is given by \[V = \frac{4}{3} \pi r^3.\]
Volume of Cones and Pyramids (Decomposing a prism)
Another way to understand the relationship between a prism and its corresponding pyramid is by dividing a cube into 6 equivalent pyramids.
Then one can use Cavalieri’s principle to generalize to any cone or pyramid.
Related Content Standards
- (8.G.9) Know the formulas for the volumes of cones, cylinders, and spheres and use them to solve real-world and mathematical problems.
- (HSG.GMD.1) Give an informal argument for the formulas for the circumference of a circle, area of a circle, volume of a cylinder, pyramid, and cone. Use dissection arguments, Cavalieri’s principle, and informal limit arguments.
- (HSG.GMD.2) Give an informal argument using Cavalieri’s principle for the formulas for the volume of a sphere and other solid figures.
- (HSG.GMD.3) Use volume formulas for cylinders, pyramids, cones, and spheres to solve problems.
11.2.4 Exercises
Use Cavalieri’s Principle and prisms to give an informal argument for the volume of a sphere.
One common formula for the circumference of a circle is \(C= 2 \pi r\) and the formula for the area of a circle is \(A=\pi r^2\). Students often confuse these two, as they both contain a 2, \(\pi\), and \(r\). Using the relationship between length and area, what is one way to tell which is which?
Perimeter and Areas of polygons.
- Create a table with the following headings: Shape name, generic drawing, perimeter formula, area formula. Fill in the table for the following shapes: triangle, square, rectangle, regular \(n\)-gon. For the generic drawing, include labels for any variables you use in your perimeter or area formulas.
- Reflect on your perimeter formulas. Do you ever multiply two or more dimensions together? Why or why not?
- Reflect on your area formulas. Do you ever multiple 3 dimensions together? Why or why not?
- Notice that when you multiply dimensions for an area formula the two dimensions are perpendicular to each other. Why does this make sense?
Use the principles of this section to derive the usual formulas for area of two-dimensional objects and volume of three-dimensional objects.