3.1 Partitions and Equivalence Relations

Figure 3.1: Sorting Candy

As a way to better understand the world, humans tend to sort information into categories or orderings. For instance, when some people see a pile of various types of M&M’s^TM they have the urge to sort them in various ways. Some people sort the candies according to their color. Others may sort them according to their type (plain, peanut, etc.). This process of sorting is a type of “partitioning” the items into distinct categories. With this categorization we want to make sure that each candy is sorted into one, and only one, type. This type of sorting can be formalized with the following definition.

3.1.1 Partitions

Definition 3.1 A partition of a set \(A\) is a finite or infinite collection of non-empty, mutually-disjoint subsets whose union is \(A\).

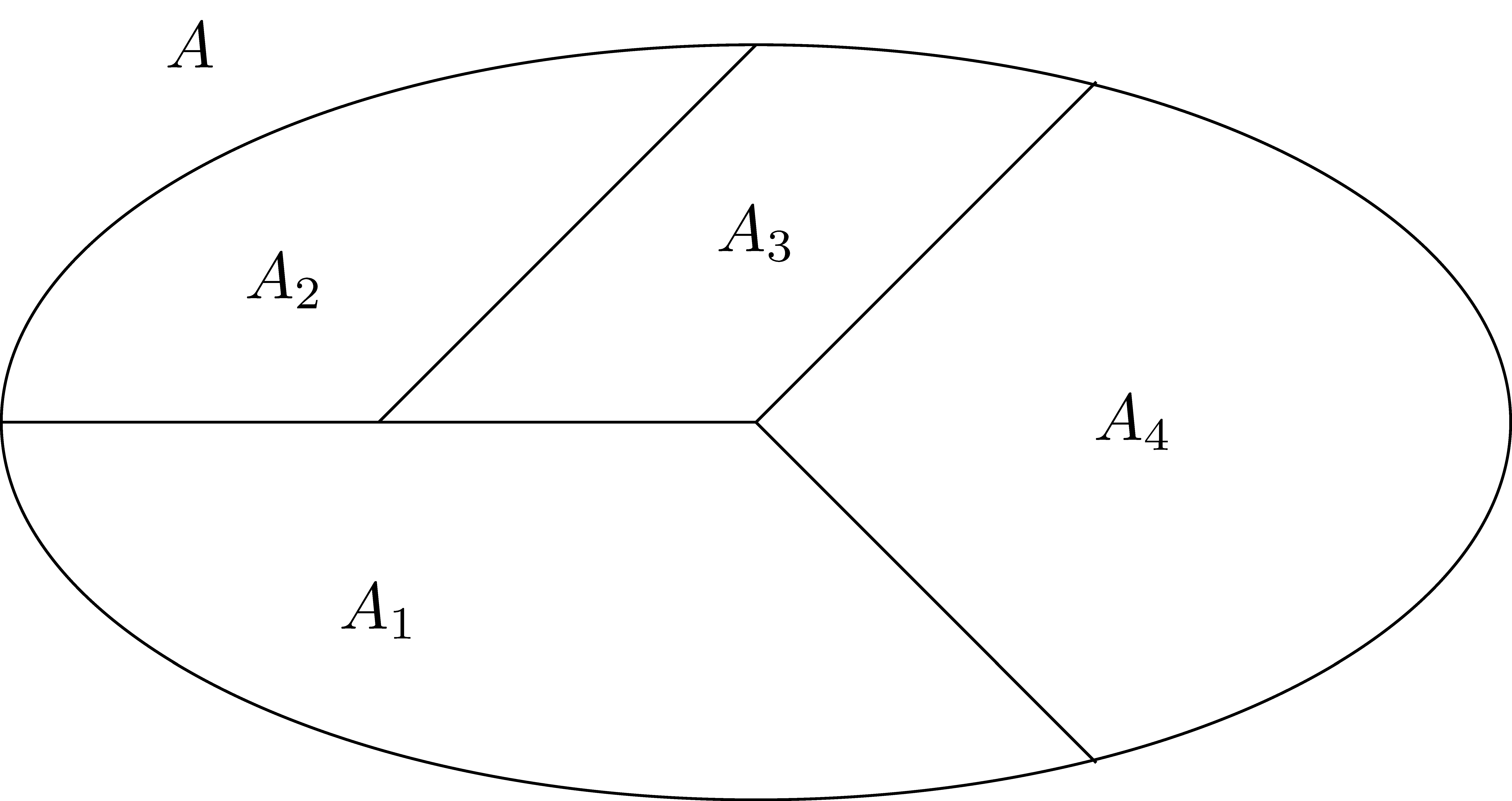
Figure 3.2: Partition of Sets

Thus, a partition of a set is a collection of subsets of the original set with several key properties.

The subsets are non-empty, meaning that each subset in the partition contains at least one element. This allows us to restrict the partition to a collection of non-trivial subsets and means partitions have a type of uniqueness.
The subsets in the partition are also mutually-disjoint which means that no element of the original set is in more than one of the subsets in the partition.
Lastly, since the union of the subsets that form the partition is \(A\), we have that every element in \(A\) is in one of these subsets.

Thus, each component of the definition of a partition is essential to defining a way to split a set into a set of categories that we find useful.

Example 3.1 If we have a set \[A=\left\{ a, 2, \alpha , \mbox{apple} , \mbox{box}, \beta, 1, 3, \gamma , \mbox{cow}, c, b \right\}\] there are some natural ways to partition the set. Here are three possible partitions.

\[A_1 = \{a,b,c\}, \: A_2 = \{1,2,3\},\: A_3 = \{\alpha, \beta, \gamma\}, \: A_4 = \{\mbox{apple} , \mbox{box}, \mbox{cow}\}\] \[A_1 = \{\mbox{apple} , \mbox{box}, \mbox{cow}\}, \: A_2 = \{a,b,c,1,2,3,\alpha,\beta,\gamma\}\] \[A_1 = \{a,1,\alpha,\mbox{apple}\}, \: A_2 = \{b,2,\beta,\mbox{box}\}, \: A_3 = \{c,3,\gamma, \mbox{cow} \}\] However, \[A_1=\{a,b,c, \mbox{apple}, \mbox{box}, \mbox{cow}\}, A_2=\{\alpha, \beta, \gamma, \mbox{apple}, \mbox{box}, \mbox{cow}\}, A_3=\{1,2,3, \mbox{apple}, \mbox{box}, \mbox{cow}\}\] is not a partition of the set because \(A_1\), \(A_2\), and \(A_3\) are not mutually disjoint.

There are many other ways to partition the set, but we do not have the space to write out all of the possible partitions of this set.

Example 3.2 Early in the K-12 mathematics curriculum we ask students to determine which integers are even and which are odd. In this situation, the set \(A\) is the set of integers (\(\mathbb{Z}\)), while the subsets that form the partition are the subset of even numbers, (\(2\mathbb{Z}\)), and odd numbers, (\(2\mathbb{Z}+1\)).

Example 3.3 If we let the set \(B\) be defined by the following list of elements, \[B = \begin{Bmatrix} \mbox{ jar}, & \mbox{ jellybean} , & \mbox{ applesauce}, & \mbox{ ape}, & \mbox{ bear}, \\ \mbox{ ball}, & \mbox{ beanbag}, & \mbox{ bag}, & \mbox{ arm} , & \mbox{ skate} , \\ \mbox{ bike}, & \mbox{ rock}, & \mbox{ rowboat}, & \mbox{ jigsaw}, & \mbox{ saw} \end{Bmatrix}\] take some time to create various partitions of the set \(B\), verifying the various properties in the definition of a partition.

In this text, we denote the partition \(\mathcal{P}\) of a set \(A\) as the union of subsets of \(A\) over some indexing set, \(I\). For example, if the partition is formed using two subsets of \(A\), then the indexing set could be \(I=\{1,2\}\). The indexing set can also be infinite. For instance, \[\mathcal{P} = \left\{ A_n \right\}_{n\in \mathbb{Z}}, \: \mbox{ where } A_n=\left\{x\in \mathbb{R}\middle \vert n\leq x < n+1 \right\}\] is a partition of the real numbers with an infinite number of sets.

It is important to note that there are usually many ways to partition a set, but the definition of partition does not impose any constraints on the uniformity or order of the subsets, only that the way we choose our subsets meets the three conditions described previously.

With our previous discussion and examples in mind, we can translate our verbal definition of a partition into a symbolic one. In particular: if \(\mathcal{P}= \left\{ U_i\right\}_{i\in I}\) is a partition of a set \(A\), where \(I\) is some indexing set that is either finite or infinite, we have the following properties

the elements of the partition are mutually disjoint: \[U_i \bigcap U_j = \emptyset \quad \mbox{if } i\neq j,\]
the union of the elements of the partition is the entire set: \[\bigcup_{i\in I} U_i = A,\]
the elements of the partition are non-empty: \[U_i \neq \emptyset \mbox{ for all } i \in I.\]

3.1.2 Relations

Up until this point we have focused on building a framework for understanding the notion of partition. In order to understand the main topics of this chapter, we also need to develop the idea of a relation. While we give the general definition of a relation and a few examples, we will focus on those relations that arise from partitions in this section. We will explore other types of relations in later sections.

Definition 3.2 Let \(A\) and \(B\) be sets. We define a relation \(R\) from \(A\) to \(B\) as a subset of \(A\times B\). We say that for elements \(a\in A\) and \(b\in B\) that \(a\) is related to \(b\), (\(aRb\)), if and only if \((a,b)\in R\). If the two sets are the same set, \(A\), then we say that \(R\) is a relation on \(A\).

Note that relations can be written in many different ways, with the most common being similar to \(a=b\), \(a<b\), \(a\tilde b\).

Here are some examples of relations in the K-12 curriculum.

Let \(A\) and \(B\) be the set of integers. We could say that \[R=\{(a,b)\in A\times B \vert a<b\},\] which defines the ‘less than’ relation of \(aRb \leftrightarrow a<b\).
Let \(A\) be the real numbers and \(B\) be the non-negative real numbers. We can let \[R=\{(x,y)\in A\times B \vert y=x^2\}.\] This is the graph of the function \(f(x)=x^2\).
Let \(A\) and \(B\) be the set of integers. We can define \[R= \{(m,n) \vert m-n=2k, \: \mbox{ for some integer } k\}.\] This relation is one where are the even numbers are related to each other and all of the odd numbers are related to each other.

3.1.3 Equivalence Relations Induced by Partitions

For the remainder of this section we will study a specific type of relation that is created by a partition, \(\mathcal{P}\), of a set, \(A\). If \(\mathcal{P}=\left\{U_i\right\}_{i\in I}\) is a partition of \(A\), we can write \(A\) as the union of a collection of non-empty, mutually disjoint subsets: \[U_i \cap U_j = \emptyset \mbox{ if } i\neq j, \: \mbox{ for each } i \in I, \: U_i\neq \emptyset, \: \mbox{ and } A=\bigcup_{i\in I} U_i.\]

Consider one of the individual subsets in the partition, say \(U_i\). Then the elements of \(U_i\), by virtue of the fact they are in the same subset, have a relationship to each other. This idea extends to the whole partition. That is, the partition induces a relation on \(A\) in the following way. For each \(a,b\in A\) we say that \(aRb\) if, and only if, there is a set \(U_i\) in the partition \(P\) such that both \(a\) and \(b\) are in \(U_i\).

The relations we create through a partition behave in ways that are of general interest in the study of mathematics.

If we choose a generic element \(a\) in \(A\), the property that \(\bigcup_{i\in I} U_i = A\) tells us that there exists \(i\in I\) such that \(a \in U_i\). So for every element \(a\in A\), we have that \(a\) is related to itself, \(aRa\). We will call this property of the relation the reflexive property.

For the second property, if we have \(a,b\in A\) such that \(aRb\), then there must be a \(U_i\in P\) with \(a,b\in U_i\). This also means that \(bRa\). When you have the property that \(aRb\) implies that \(bRa\), we say that the relation has the symmetric property.

The third property of relations that we define derives from the property of partitions that \[U_i \bigcap U_j = \emptyset \Leftrightarrow i\neq j.\] If \(a,b,c\in A\) such that \(aRb\) and \(bRc\), then we have that there are sets \(U_i\) and \(U_j\) in the partition such that \(a\) and \(b\) are both in \(U_i\) and \(b\) and \(c\) are both in \(U_j\). Since \(b\) is in both \(U_i\) and \(U_j\), \(U_i \cap U_j \neq \emptyset\) and so \(i=j\). This would then imply that \(aRc\). This property that the combination of \(aRb\) and \(bRc\) implies that \(aRc\) is called the transitive property of relations.

Not all relations have these three properties of reflexive, symmetric, and transitive. Those relations that have all three properties are called equivalence relations.

We have therefore proven that a partition of a set induces an equivalence relation on that set.

3.1.4 Partitions Induced by Equivalence Relations

The concept of equivalence relation is one that transcends much of mathematics and we often consider things as being the “same” with respect to some property if there is an equivalence relation under which they are related. One location that this appears in the elementary school curriculum is in regards to rational numbers. We think of \(\frac{1}{2}\) and \(\frac{2}{4}\) as being the same rational number, but written in a different way. Along these lines we say that two rational expressions \(\frac{a}{b}\) and \(\frac{c}{d}\) are equivalent if and only if \(ad=bc\). This creates and equivalence relation between these rational expressions that are used to create the rational numbers.

Similarly, if a relation, \(R\), on a set, \(A\), is an equivalence relation, then one can generate an induced partition, \(\mathcal{P}\), as follows. For each \(a\in A\) we define the set \[[a]_R := \left\{ b\in A \middle \vert aRb\right\}.\] We call this set, \([a]_R\), the equivalency class of \(a\) under the relation \(R\).

Since \(R\) is an equivalence relation, it is reflexive and so \(a \in [a]_R\) causing \([a]_R \neq \emptyset\). Since \(a\in [a]_R\), we have that \[\bigcup_{a\in A} [a]_R = A.\] Thus to show that \(\mathcal{P} = \left\{ [a]_R \middle \vert a \in A\right\}\) is a partition of \(A\), we need to show that for \(a,b\in A\) that \([a]_R=[b]_R\) or \([a]_R\bigcap [b]_R = \emptyset\).

If \([a]_R \bigcap [b]_R \neq \emptyset\), then we need to prove that two sets to be equal.

Let us assume that there exists a \(c\in [a]_R \bigcap [b]_R\).

Let \(d\in [a]_R\). So \(a R d\). \(c\) is also in \([a]_R\) and so \(aRc\). Since \(R\) is symmetric and \(aRd\), \(dRa\). We now have that \(dR c\) using transitive property. \(c\) is also in \([b]_R\) and so \(bRc\). Using the symmetric property, we have \(cR b\). Combining this with \(dRc\) and using the transitive property we have \(dR b\). Using the symmetric property we have \(bR d\). So \(d\in [b]_R\). Therefore, \([a]_R \subseteq [b]_R\).

Using very similar arguments we can prove that \([b]_R \subseteq [a]_R\).

So if the intersection is nonempty, the two sets are the same set.

We have thus proven the following theorem showing the connection between equivalence classes and partitions.

Theorem 3.1 If \(R\) is an equivalence relation on a set \(A\), then \[P = \left\{ [a]_R \middle \vert a \in A\right\}\] is a partition of \(A\).

Similarly, if \(P= \left\{ U_i \middle \vert i \in I\right\}\) is a partition on a set \(A\), then the relation \(R\) defined by \[aRb \Leftrightarrow \mbox{ there exists } i \in I \mbox{ such that } a,b \in U_i\] is an equivalence relation.

In summary, we have defined a relation \(R\) from \(A\) to \(B\) as a subset of \(A\times B\), and that \(a\) is related to \(b\), (\(aRb\)), if and only if \((a,b)\in R\). If the two sets are the same set, \(A\), then we say that \(R\) is a relation on \(A\).

We also defined the following three properties of a relation, \(R\), on a set \(A\):

Reflexive. The relation \(R\) is reflexive if \(aRa\) for all \(a\in A\).
Symmetric. The relation \(R\) is symmetric if \(aRb\) implies that \(bRa\) for all \(a,b\in A\).
Transitive. The relation \(R\) is transitive if \(aRb\) and \(bRc\) imply that \(aRc\) for \(a,b,c\in A\).

Note: to prove that a relation satisfies one of these properties, you need to show that the statement is true for all possible elements. To prove that a property is not satisfied, a single counter example is sufficient.

A relation is an equivalence relation if, and only if, it satisfies all three of these properties.

3.1.5 Ordered Sets and Relations

Another type of relation is one that creates an order, or ranking, of the set. A common mathematical topic in this regards are the concepts of “less than” and “less than or equal to”.

We will first explore the relation of “less than”. Since a number cannot be less than itself we see that the relation is not reflexive. We also know that \(a<b\) and \(b<a\) cannot both be true and so the relation is not symmetric. However, if \(a<b\) and \(b<c\), we do have that \(a<c\). So this relation of “less than” is transitive. Thus the familiar relation of “less than” is one which is transitive but not reflexive or symmetric.

When we expand the relation to that of “less than or equal to”, we add that \(a\leq a\), resulting in the relation being reflexive. So this is a common relation that is reflexive and transitive, but not symmetric. For example, \(1\leq 2\), but \(2\) is not less than or equal to \(1\).

Definition 3.3 We define an order on a set, \(A\), to be a relation, denoted by \(<\), with the following properties.

If \(x\) and \(y\) are two elements of \(A\), then one, and only one, of the statements \[x<y, \quad x=y, \quad, y<x\] is true.
If \(x,y,z \in A\), and if \(x<y\) and \(y<z\), then \(x<z\).

If a set has an order defined on the set, then we say that it is an ordered set.

Such an order forms a relation that is transitive, but not symmetric or reflexive. As a convenient notation, we will write \(x\leq y\) as the negation of \(y<x\). We then see that it is equivalent to the statement that (\(x<y\) or \(x=y\)).

Definition 3.4 (Well-Ordering Property) A set, \(A\), together with an order, \(<\), satisfies the well-ordering property if every non-empty subset of \(A\) has a least element. Equivalently, if \(S\subseteq A\) with \(S\neq \emptyset\), then there exists an element \(s_0\in S\) such that \(s_0 \leq s\) for all \(s\in S\).

We will see in Chapter 4 that the natural numbers, \(\{0,1,2,3,\ldots\}\), satisfy the well-ordering property, but the real numbers do not. For instance, \(\{x\in \mathbb{R}\vert x>1\}\) does not have a least element. This means that in some way, a set needs to be discrete in order to satisfy a well-ordering property.

For sets that are not discrete, we would like to have a similar property.

Definition 3.5 Let \(A\) be an ordered set and let \(S\subseteq A\). If there exists an \(\alpha \in A\) such that \(x\leq \alpha\) for all \(x\in S\), then we say that \(S\) is bounded above and that such an \(\alpha\) is an upper bound of \(S\).

We can similarly define bounded below and lower bound using opposite inequalities.

Definition 3.6 (Least-Upper-Bound Property) An ordered set \(A\) is said to have the least-upper-bound property if for every non-empty subset \(S\subseteq A\) that is bounded above, there exists an element \(s_0\in S\) such that \(s_0\) is an upper bound of \(S\) and if \(\alpha\) is an upper bound of \(S\), then \(s_0\leq \alpha\). Such an \(s_0\) is called the least-upper-bound of \(S\).

We will see in Chapter 4 that the real numbers satisfy the least-upper-bound property, while the rational numbers do not.

3.1.6 Exercises

For each of the following relations, determine if the relation is reflexive, symmetric, and/or transitive.
1. Let \(S\) be a relation defined on \(\mathbb{R}\) by \[xSy \Leftrightarrow x^2=y^2.\]
2. Let \(T\) be a relation defined on \(\mathbb{R}\) by \[xTy \Leftrightarrow x<y^2.\]
3. Let \(U\) be a relation defined on \(\mathbb{Z}\) by \[mUn \Leftrightarrow mn>0.\]
4. Let \(V\) be a relation defined on \(\mathbb{R}^2\) by \[ (x,y)V(w,z) \Leftrightarrow x^2+y^2 \leq w^2+z^2.\]
For the Natural numbers, \(\mathbb{N}= \{0, 1, 2, 3, \ldots \}\), define the relation on \(\mathbb{N}\) by \(m\) is related to \(n\) if and only if \(m\) is a factor of \(n\).
1. Is the relation reflexive?
2. Is the relation symmetric?
3. Is the relation transitive?
4. Do any of your answers change if we remove \(0\) and \(1\) from the set?
Let \(S=\{a,b\}\). List out all of the possible relations on \(S\) and determine which relations are reflexive, symmetric, and/or transitive.
Define a relation \(\sim\) on \(\mathbb{R}\times (\mathbb{R}-\{0\})\) by \[(x,y) \sim (z,w) \Leftrightarrow xw=yz.\]
1. Show that this relation is an equivalence relation.
2. Give a description of the partition of \(\mathbb{R}\times (\mathbb{R}\setminus \{0\})\) induced by this equivalence relation.
3. Why do we not allow \(0\) in the second part of the ordered pairs?
Determine which of the following collections of sets form a partition of \(\mathbb{R}\times \mathbb{R}\). For those that do form a partition, define the equivalence relation (you do not need to prove each of the properties). For those that do not form a partition, what is one property that fails.
1. For \(c\in \mathbb{R}\), let \(h_c= \{ (x,y)\in \mathbb{R}^2 \vert y=c\}\), and let \(\mathcal{C} = \{h_c\}_{c\in \mathbb{R}}\).
2. For \(m\in \mathbb{R}\), let \(s_m=\{ (x,y)\in \mathbb{R}^2 \vert y=mx\}\), and let \(\mathcal{D}= \{s_m\}_{m\in \mathbb{R}}\).
3. For \(r\in [0,\infty)\), let \(C_r=\{ (x,y) \in \mathbb{R}^2 \vert x^2+y^2=r^2\}\), and let \(\mathcal{E}=\{C_r\}_{r\in [0,\infty)}\).
(For students who have knowledge of linear algebra) Let \(M_{2,2}\) be the set of \(2 \times 2\) matrices with real coefficients. For each of the following, prove that it is an equivalence relation, or show that one of the properties of equivalence relations does not hold.
1. For matrices \(A\) and \(B\) in \(M_{2,2}\), let \(A \sim B\) if and only if \(\mathrm{det}(A)=\mathrm{det}(B)\).
2. For matrices \(A\) and \(B\) in \(M_{2,2}\), let \(A \sim B\) if and only if \(\mathrm{tr}(A)=\mathrm{tr}(B)\).
3. For matrices \(A\) and \(B\) in \(M_{2,2}\), let \(A \sim B\) if and only if the eigenvalues of \(A\) are the same as the eigenvalues of \(B\).