10.3 Euclid’s Basic Constructions
Now that we have established the role of definitions and axioms, we will look at how those definitions and axioms are used to prove geometric theorems using Euclid’s system. Euclid’s geometry is abstract, and fits within platonism philosophy, in that one cannot see the real objects of a point or a line (as they have no breadth). However, we represent points and lines with sensual symbols that we can draw on a piece of paper. So in the proofs we must remember that the drawings are not the proof and are not the actual points, lines, and circles. They are instead representations of points, lines, and circles in order to assist in the communication of the mathematical proof.


Figure 10.3: Straightedge and Compass
To assist in the representations we often use a straight edge (usually a ruler ignoring the markings) to represent straight lines and we use a compass (either collapsible or fixed) to describe a circle with a fixed center and radius.
Related Content Standards
- (HSG.CO.12) Make formal geometric constructions with a variety of tools and methods (compass and straightedge, string, reflective devices, paper folding, dynamic geometric software, etc.). Copying a segment; copying an angle; bisecting a segment; bisecting an angle; constructing perpendicular lines, including the perpendicular bisector of a line segment; and constructing a line parallel to a given line through a point not on the line.
We can also use dynamic geometry software like Desmos or GeoGebra to create representations of lines and circles.
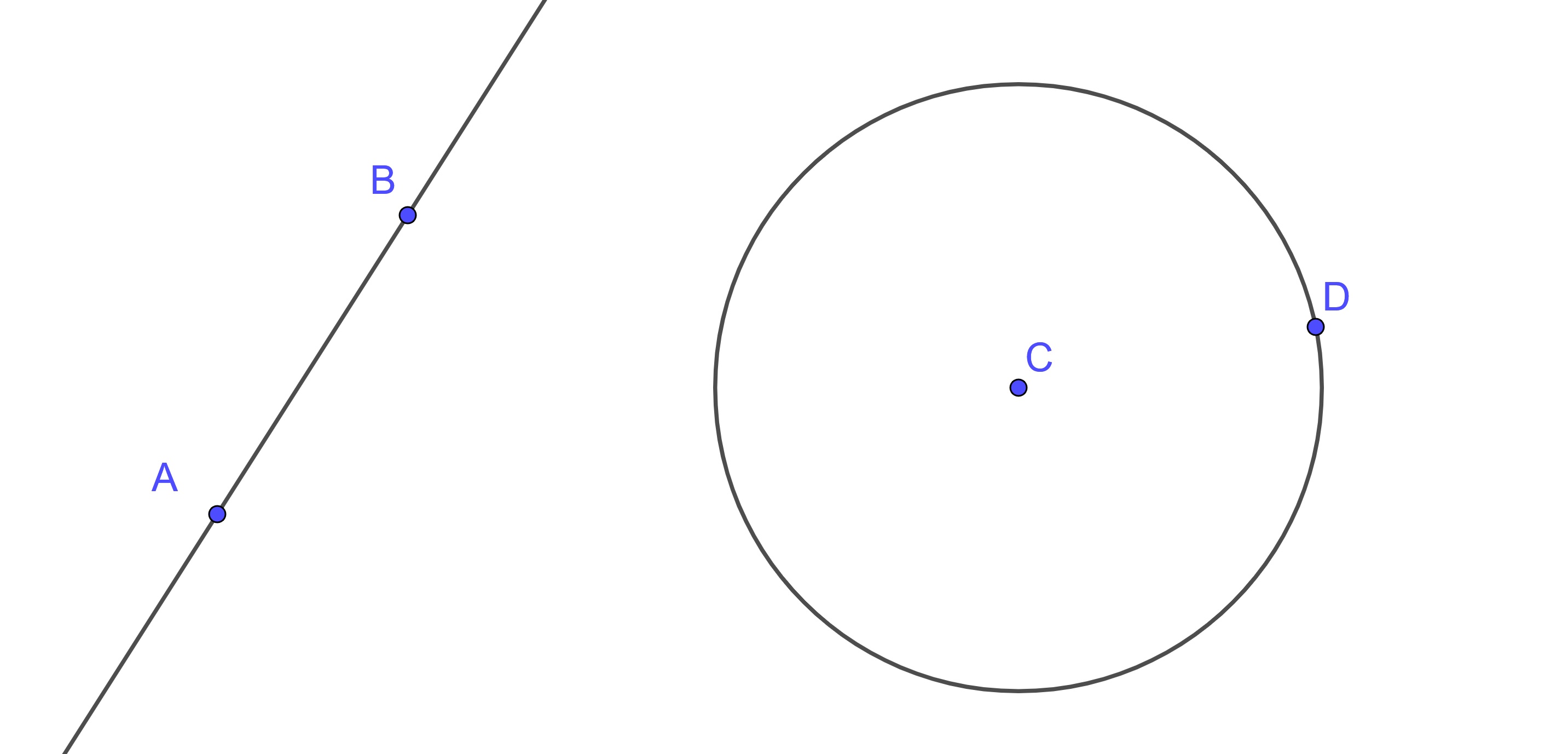
Figure 10.4: Line and Circle Constructed using GeoGebra
As we work through some of the Propositions from Euclid’s Elements we will use some of these representations within the proofs in order to communicate the ideas of the proof. For each of the propositions, we will give the proposition using the translation of Heath (Heath, 1908a) in order to better understand the historical context. We will then give a more modern version of the proposition.
You can also find many of these propositions and proofs at http://aleph0.clarku.edu/~djoyce/elements. Many students find it useful to use this resource as they work through Euclid’s propositions.
10.3.1 Initial Propositions
We will include the proofs of some of Euclid’s initial propositions below in order to understand the idea of the axiomatic method and to demonstrate some of Euclid’s basic constructions. Proofs of the remainder of the propositions can easily be found online.
Proposition 10.1 (Euclid's Proposition 1: Construction of Equilateral Triangle) On a given finite straight line to construct an equilateral triangle.
This proposition states that if you are given a line segment, you can use a compass and straightedge to construct and equilateral triangle where the line segment is one of the sides.
Proof. We start with a given finite straight line \(AB\), labeled by its endpoints. Such a finite straight line exists by Postulate 1.
Postulate 3 implies that we can describe a circle centered at \(A\) through the point \(B\) and a second circle centered at \(B\) through the point \(A\).
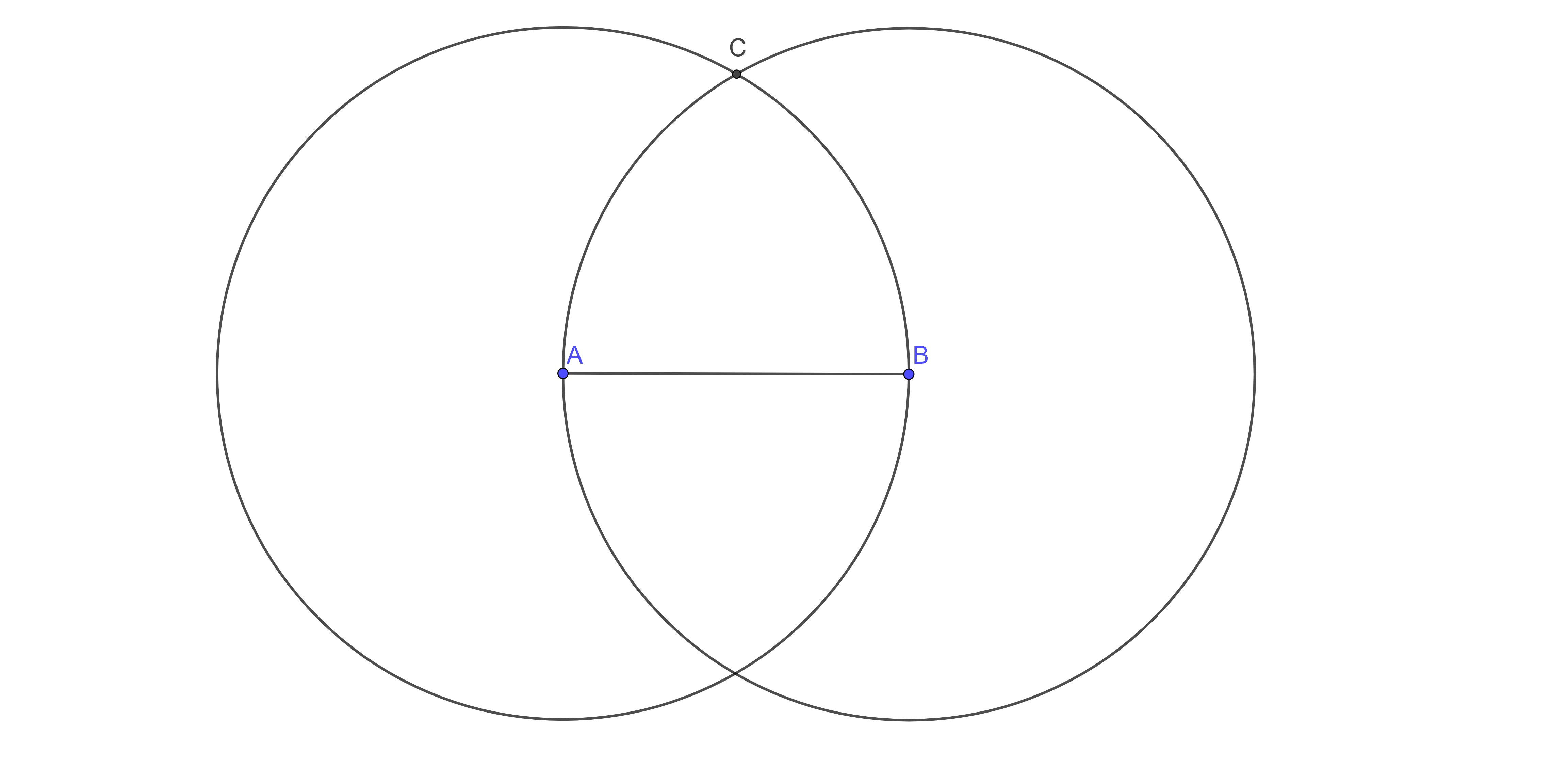
The point \(C\) is an intersection of the two circles. The existence of such a point, and that it lies in the same plane as \(AB\) are some of the first issues raised with the Euclidean system of axioms that are resolved in the Hilbert and SMSG systems.
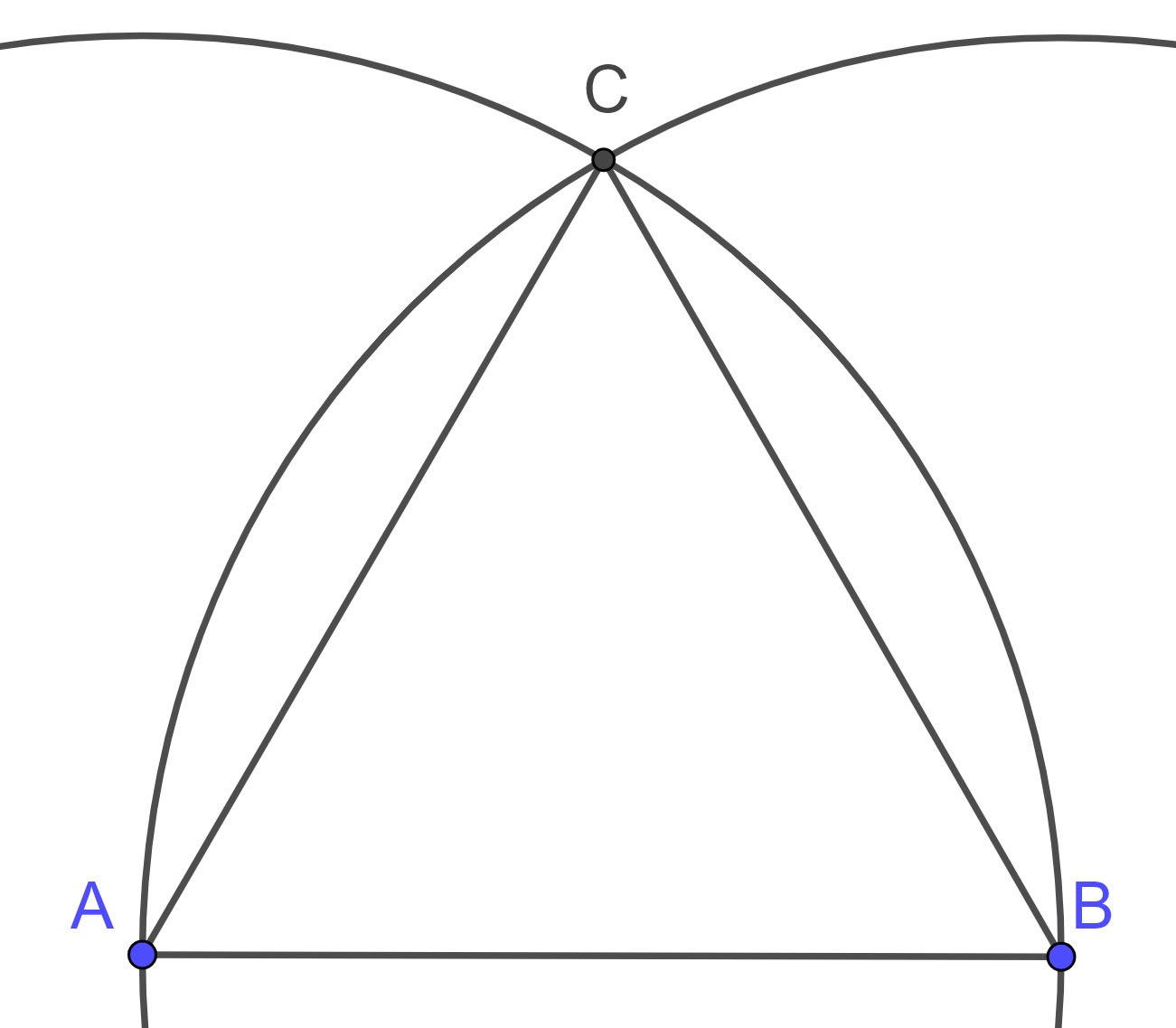
Since \(C\) lies on the circle centered at \(A\) through the point \(B\), \(AC\) must be the same length as \(AB\). Since \(C\) also lies on the circle centered at \(B\) through \(A\), \(BC\) must be the same length as \(BA\). Then using Common Notions 1 and 4 we can conclude that the three sides of \(\triangle ABC\) have the same length and so form an equilateral triangle.
Euclid’s second and third propositions allow us to construct a segment of the same length as a given segment at another point and along a line through that point.
Proposition 10.2 (Euclid's Proposition 2) To place at a given point (as an extremity) a straight line equal to a given straight line.
Proposition 10.3 (Euclid's Proposition 3) Given two unequal straight lines, to cut off from the greater a straight line equal to the less.
Euclid’s proof of Proposition 4 uses a technique called superposition. In our current language, Euclid considers a translation to maintain distances and angles without proving such. We can note that this proposition is the 15th postulate in the SMSG axioms as it is something that is difficult to prove geometrically without analytic techniques using a coordinate plane.
Proposition 10.4 (Euclid's Proposition 4: SAS Triangle Congruence) If two triangles have the two sides equal to two sides respectively, and have the angles contained by the equal straight lines equal, they will also have the base equal to the base, the triangle will be equal to the triangle, and the remaining angles will be equal to the remaining angles respectively, namely those which the equal sides subtend.
10.3.2 Isosceles Triangles
We can begin using SAS triangle congruence to prove results regarding isosceles triangle. While isosceles triangles are defined by Euclid as triangles with exactly two equal sides, the next two propositions show that these could be defined equivalently by having exactly two equal angles. We first show that two equal sides implies two equal angles.
Proposition 10.5 (Euclid's Proposition 5) In isosceles triangles the angles at the base are equal to one another, and, if the equal straight lines be produced further, the angles under the base will be equal to one another.
As you read through the proof from Heath’s translation of Euclid’s Elements (1908a, p. 251), rewrite the proof using modern terminology and verify the truthfulness of each statement based upon the prior Propositions.
Proof. Let \(\triangle ABC\) be an isosceles triangle having the side \(AB\) equal to the side \(AC\), and let the straight lines \(BD\) and \(CE\) be produced further in a straight line with \(AB\) and \(AC\).
I say that the angle \(\angle ABC\) equals the angle \(\angle ACB\), and the angle \(\angle CBD\) equals the angle \(\angle BCE\).
Take an arbitrary point \(F\) on \(BD\). Cut off \(AG\) from \(AE\) the greater equal to \(AF\) the less, and join the straight lines \(FC\) and \(GB\).
Since \(AF\) equals \(AG\), and \(AB\) equals \(AC\), therefore the two sides \(FA\) and \(AC\) equal the two sides \(GA\) and \(AB\), respectively, and they contain a common angle, the angle \(\angle FAG\).
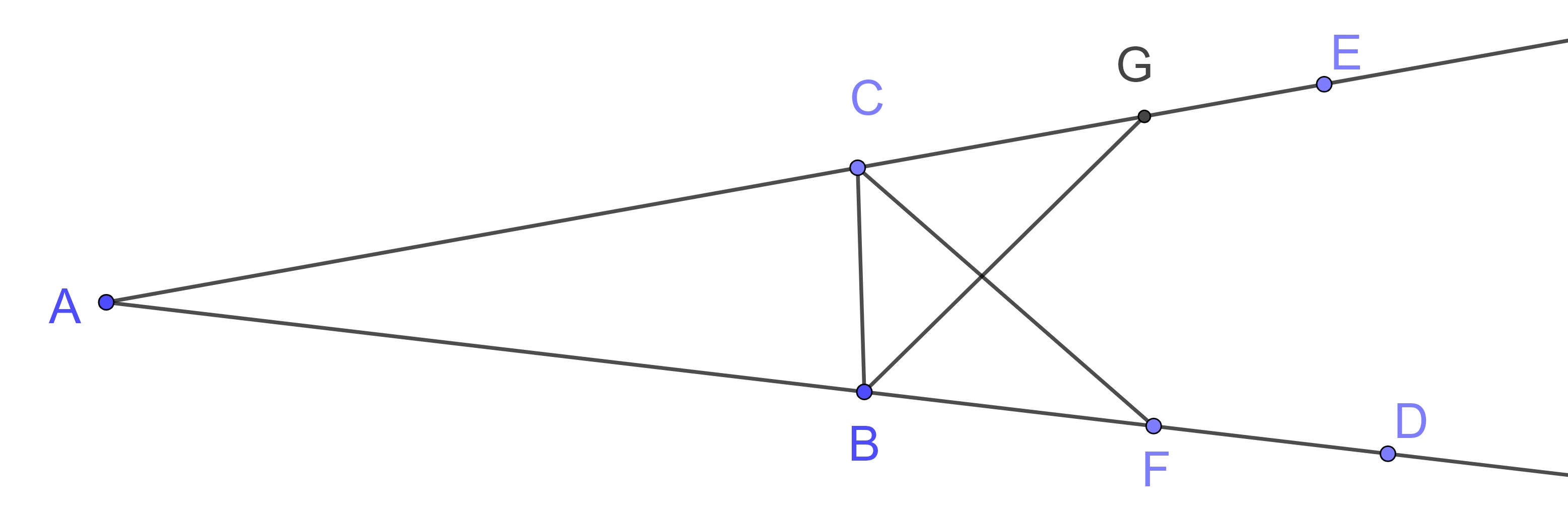
Therefore, the base \(FC\) equals the base \(GB\), the triangle \(\triangle AFC\) equals the triangle \(\triangle AGB\), and the remaining angles equal the remaining angles respectively, namely those opposite the equal sides, that is, the angle \(\angle ACF\) equals the angle \(\angle ABG\), and the angle \(\angle AFC\) equals the angle \(\angle AGB\).
Since the whole \(AF\) equals the whole \(AG\), and in these \(AB\) equals \(AC\), therefore the remainder \(BF\) equals the remainder \(CG\).
But \(FC\) was also proved equal to \(GB\), therefore the two sides \(BF\) and \(FC\) equal the two sides \(CG\) and \(GB\) respectively, and the angle \(\angle BFC\) equals the angle \(\angle CGB\), while the base \(BC\) is common to them. Therefore the triangle \(\triangle BFC\) also equals the triangle \(\triangle CGB\), and the remaining angles equal the remaining angles respectively, namely those opposite the equal sides. Therefore the angle \(\angle FBC\) equals the angle \(\angle GCB\), and the angle \(\angle BCF\) equals the angle \(\angle CBG\).
Accordingly, since the whole angle \(\angle ABG\) was proved equal to the angle \(\angle ACF\), and in these the angle \(\angle CBG\) equals the angle \(\angle BCF\), the remaining angle \(\angle ABC\) equals the remaining angle \(\angle ACB\), and they are at the base of the triangle \(\triangle ABC\). But the angle \(\angle FBC\) was also proved equal to the angle \(\angle GCB\), and they are under the base.
Therefore, in isosceles triangles, the angles at the base equal one another, and, if the equal straight lines are produced further, then the angles under the base equal one another.
We now need to prove the converse that a triangle with two equal angles also has two equal sides.
Proposition 10.6 (Euclid's Proposition 6) If in a triangle two angles be equal to one another, the sides which subtend the equal angles will also be equal to one another.
Proof. Let \(\triangle ABC\) be a triangle having the angle \(\angle ABC\) equal to the angle \(\angle ACB\).
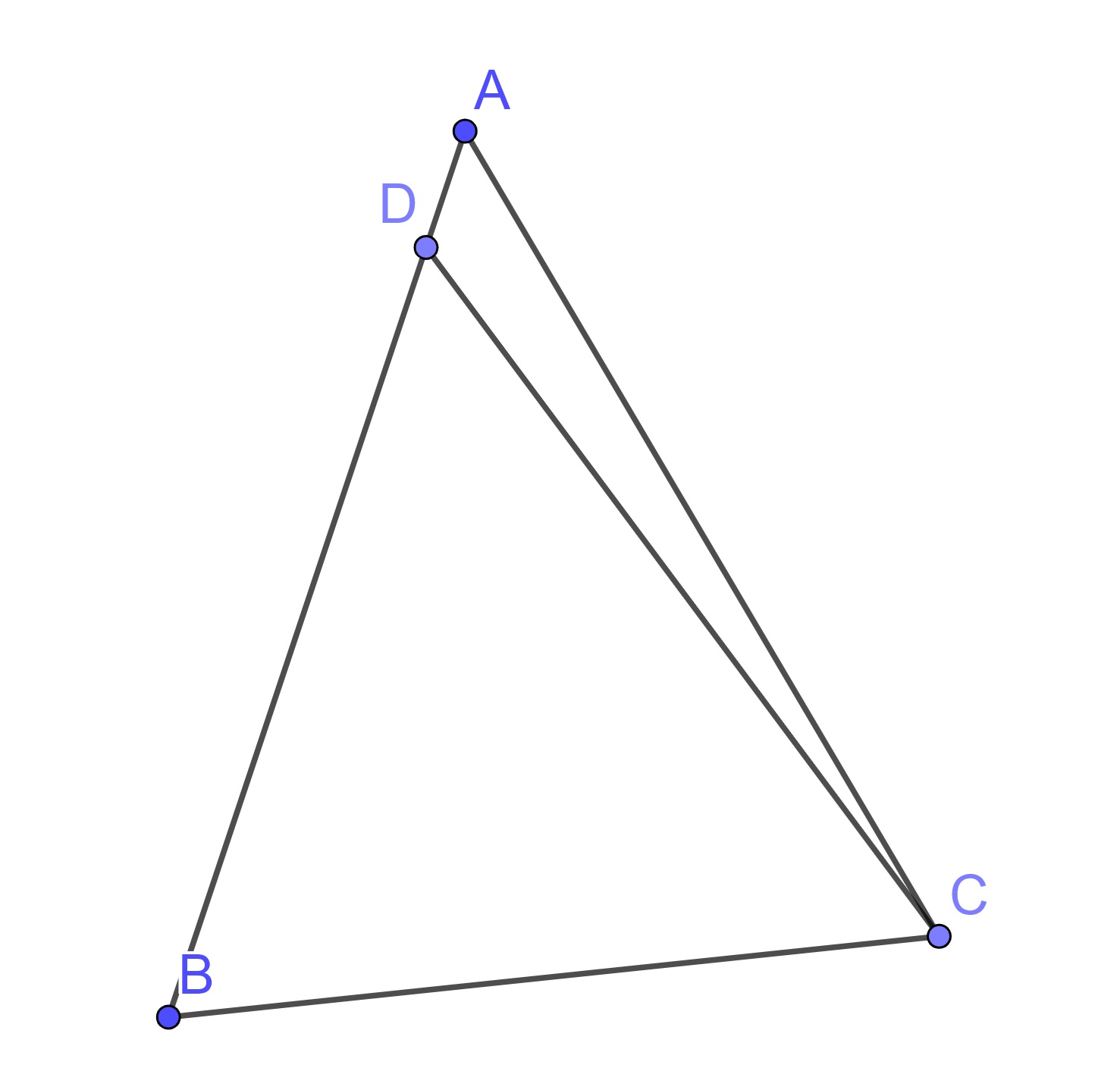
If \(AB\) does not equal \(AC\), then one of them is greater. Let \(AB\) be greater. Cut off \(DB\) from \(AB\) the greater equal to \(AC\) the less, and join \(DC\).
Since \(DB\) equals \(AC\), and \(BC\) is common, therefore the two sides \(DB\) and \(BC\) equal the two sides \(AC\) and \(CB\) respectively, and the angle \(\angle DBC\) equals the angle \(\angle ACB\). Therefore, the base \(DC\) equals the base \(AB\), and the triangle \(\triangle DBC\) equals the triangle \(\triangle ACB\), the less equals the greater, which is absurd. Therefore \(AB\) is not unequal to \(AC\), it therefore equals it.
Therefore if in a triangle two angles equal one another, then the sides opposite the equal angles also equal one another.
10.3.3 Side-Side-Side Congruence
We will skip the proofs of the next two propositions, as the proofs do not add much to our understanding. However, we will include the statements of the propositions as they will be very useful later.
Proposition 10.7 (Euclid's Proposition 7) Given two straight lines constructed on a straight line (from its extremities) and meeting in a point, there cannot be constructed on the same straight line (from its extremities), and on the same side of it, two other straight lines meeting in another point and equal to the former two respectively, namely each to that which has the same extremity with it.
This first Proposition is a little confusing, but it is stating that if one of the sides of a triangle is given, and the lengths of the other two sides is also given, then one can construct two possible triangles with that information. One on each side of the given side. The next proposition uses this to prove that any two triangles that have the same side measures are congruent to each other, since the equal side lengths force equality of the measures of the angles.
Proposition 10.8 (Euclid's Proposition 8: SSS Triangle Congruence) If two triangles have the two sides equal to two sides respectively, and have also the base equal to the base, they will also have the angles equal which are contained by the equal straight lines.
10.3.4 Angles
With the propositions in this section, we will look at some of the important constructions regarding angles, points, and sides.
Our first construction bisects angles.
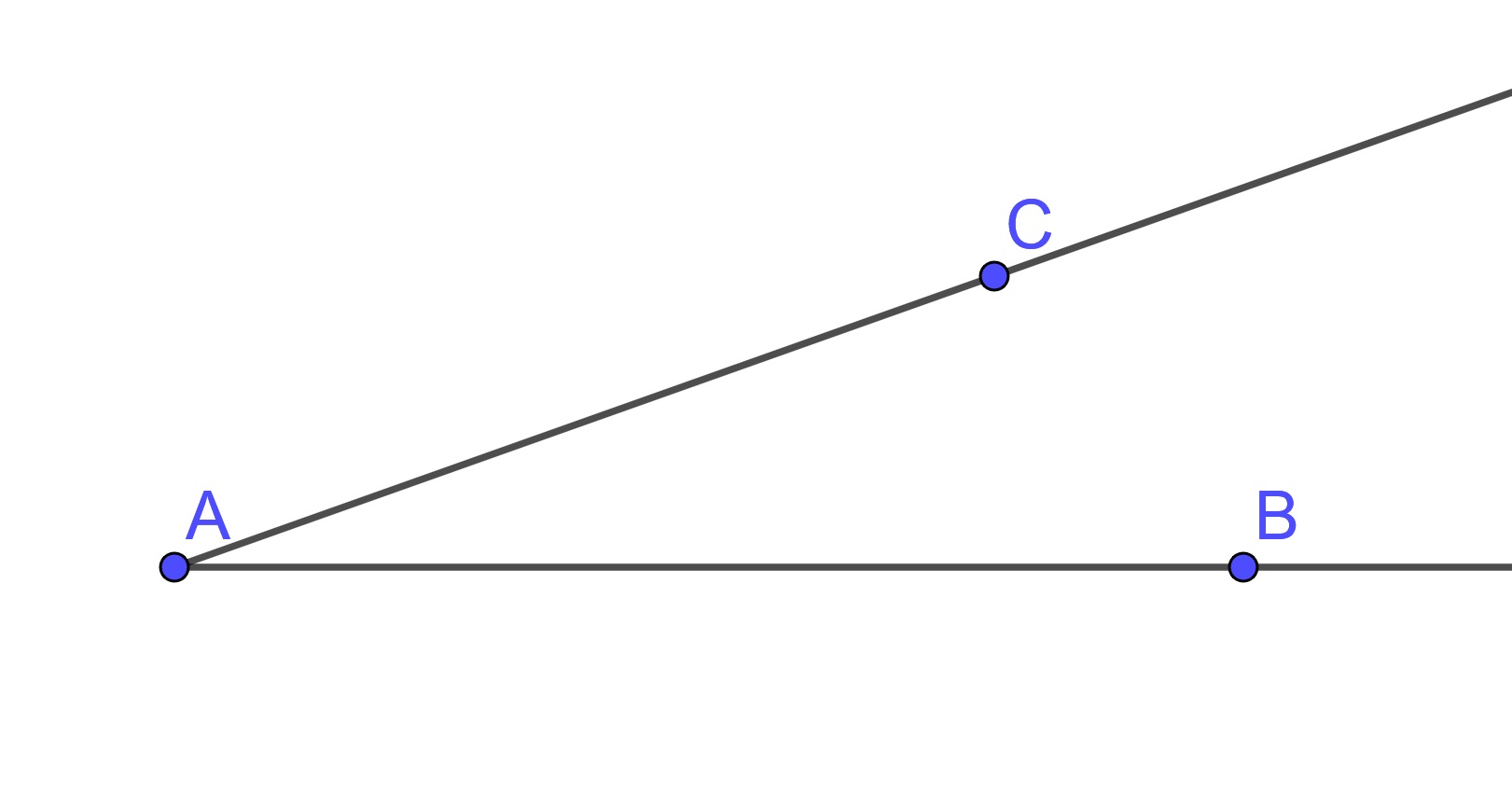
Proposition 10.9 (Euclid's Proposition 9: Construction of Angle Bisector) To bisect a given rectilinear angle.
Proof. Let \(\angle BAC\) be a given rectilinear angle (an angle contained inside two lines).
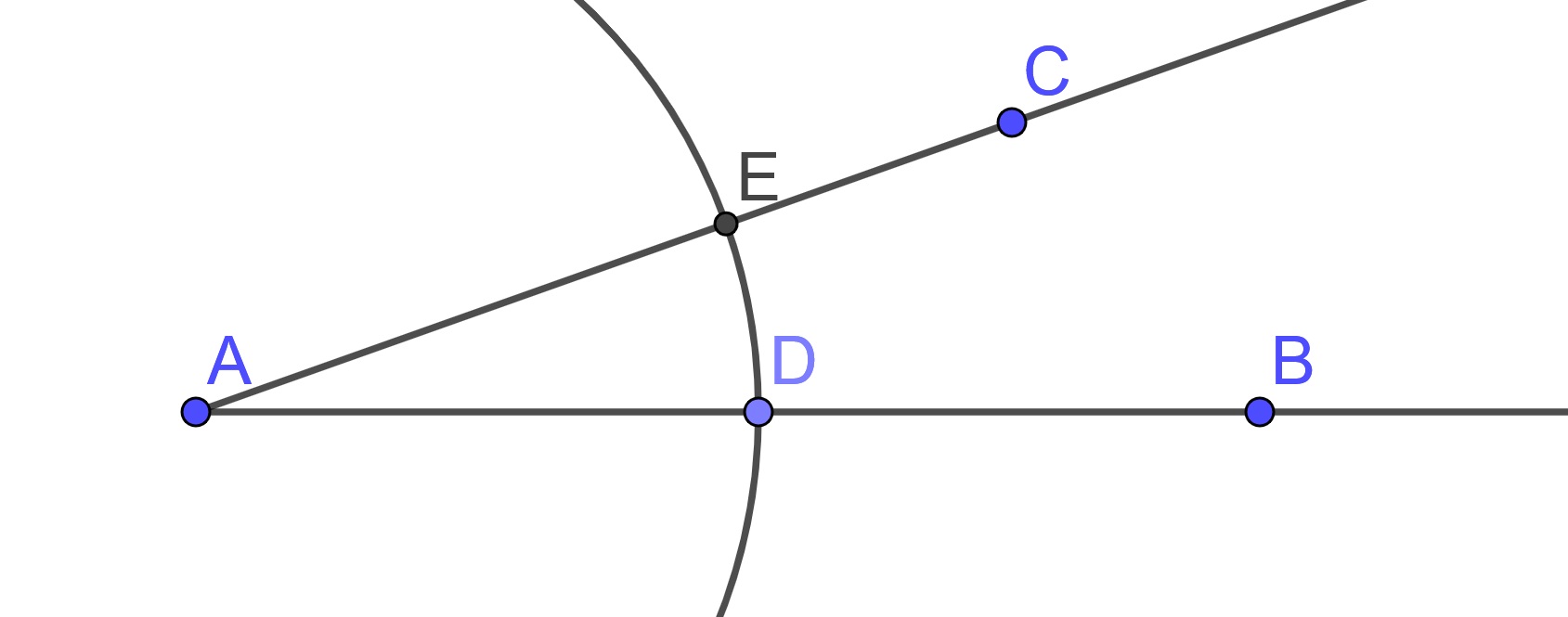
Then we can construct a circle centered at \(A\) whose radius is less than either \(AB\) or \(AC\). We can then label the point at which the circle intersects \(AB\) as \(D\) and the point at which the circle intersects \(AC\) as \(E\).
We can then construct a circle centered at \(D\) through the point \(E\) and a circle centered at \(E\) through the point \(D\). These two circles intersect at a point that we will label \(F\).
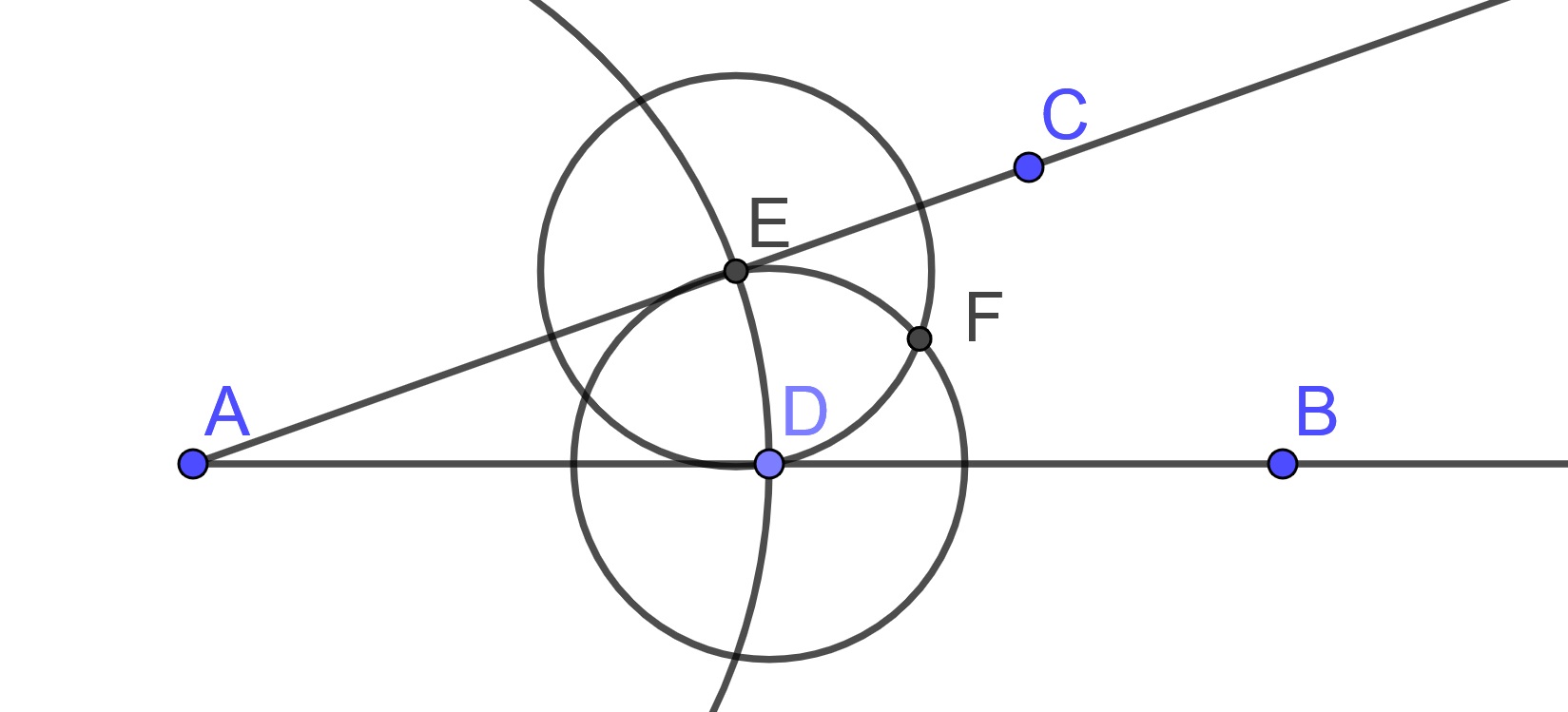
We now focus on the triangles \(\triangle ACD\) and \(\triangle AEF\).
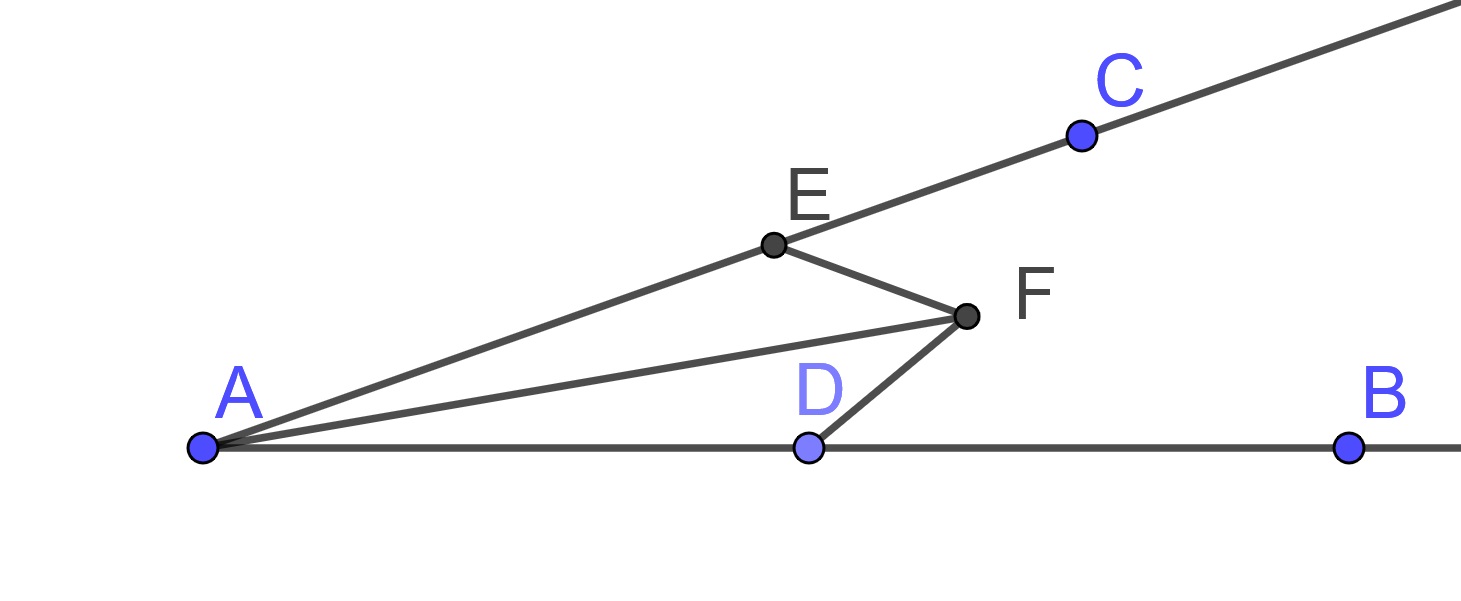
We know that \(AE\) and \(AD\) are equal because \(D\) and \(E\) are both on a circle centered at \(A\). Since \(F\) is an intersection of the circles centered at \(D\) and \(E\), \(EF\) is equal to \(DF\). Since \(AF\) is equal to \(AF\) we have the sides of the two triangles all being equal. By Proposition 8 (SSS), we have that \(\triangle ACD\) and \(\triangle AEF\) are congruent and so \(\angle EAF\) equals \(\angle DAF\). So \(AF\) bisects the angle \(\angle BAC\)
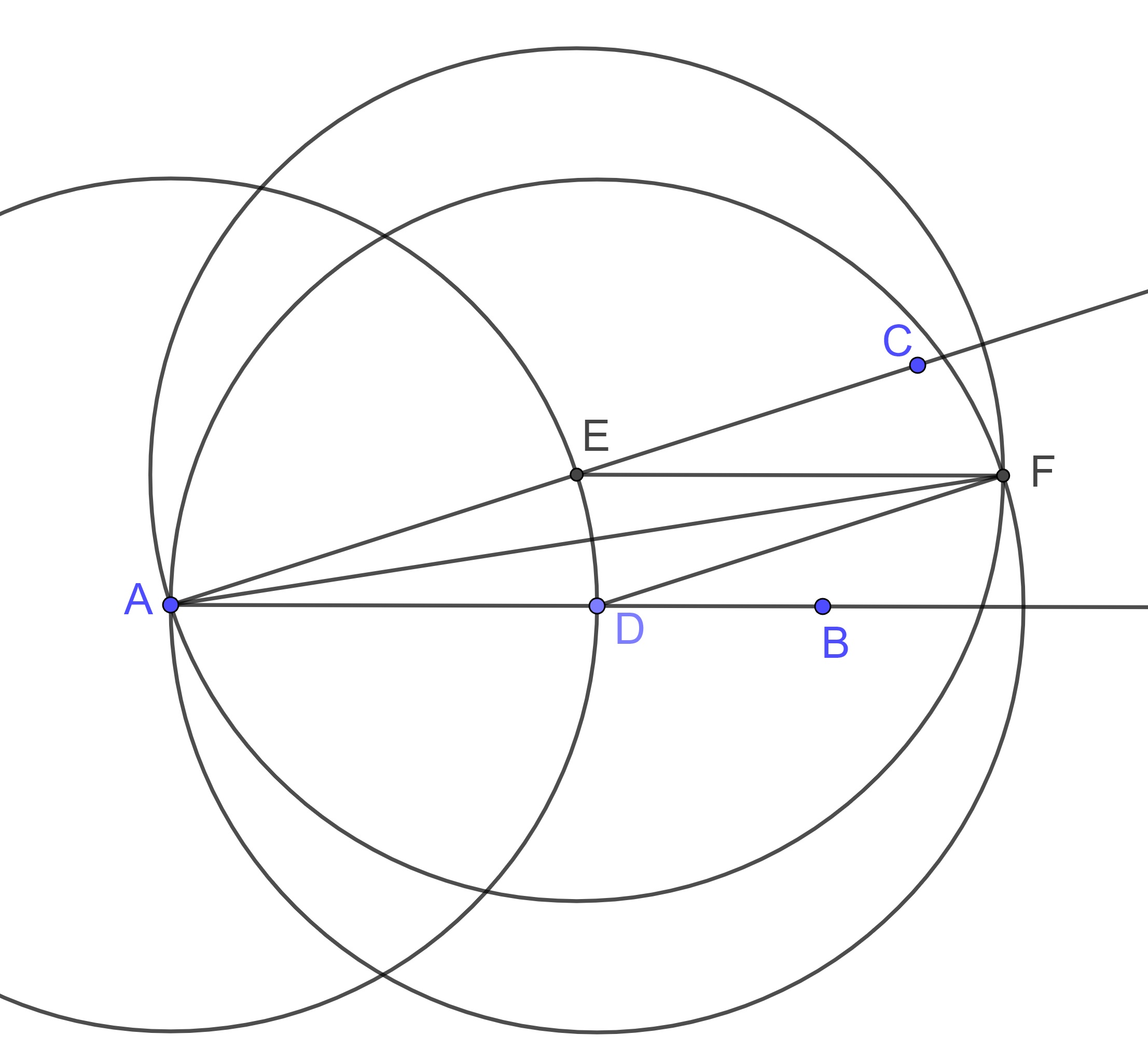
Another option for the construction process is that the circles centered at \(D\) and \(E\) pass through the point \(A\). The other point of intersection for these circles can be labeled \(F\).
The segment \(AF\) bisects the angle \(\angle BAC\). We will show later that \(AEFD\) forms a rhombus, generating parallel lines among other things.
10.3.5 Perpendicular Lines
The next few propositions involve the construction of perpendicular lines. If we start with a finite straight line \(AB\), we can use the following construction to create the perpendicular bisector. We will leave the details of the proof to the reader to work through.
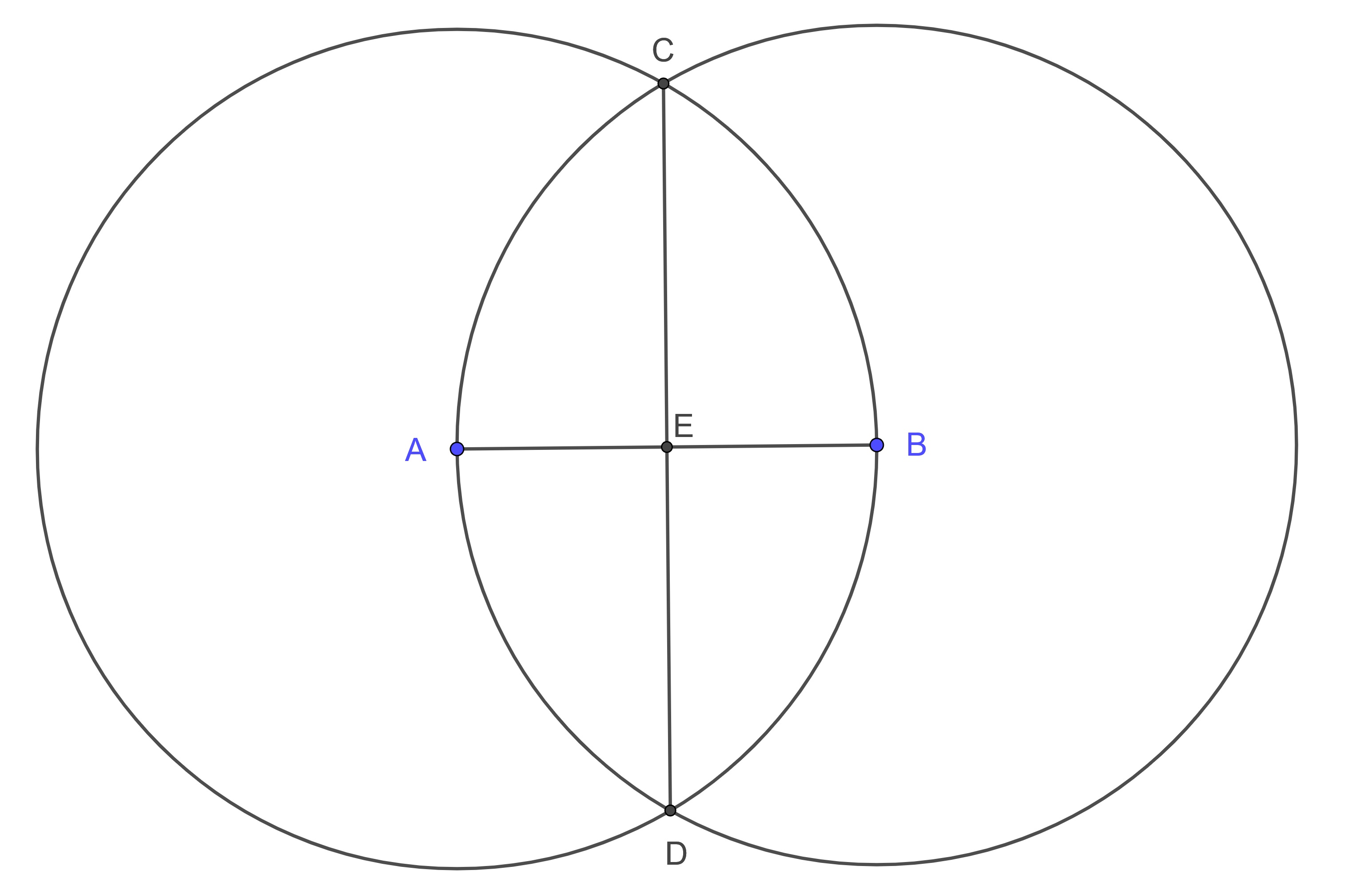
Proposition 10.10 (Euclid's Proposition 10: Construction of Perpendicular Bisector) To bisect a given finite straight line.
Proposition 10.11 (Euclid's Proposition 11: Construction of a Perpendicular Line) To draw a straight line at right angles to a given straight line from a given point on it.
We will not give the details of the proof, but will include the appropriate visual construction that gives the main ideas.
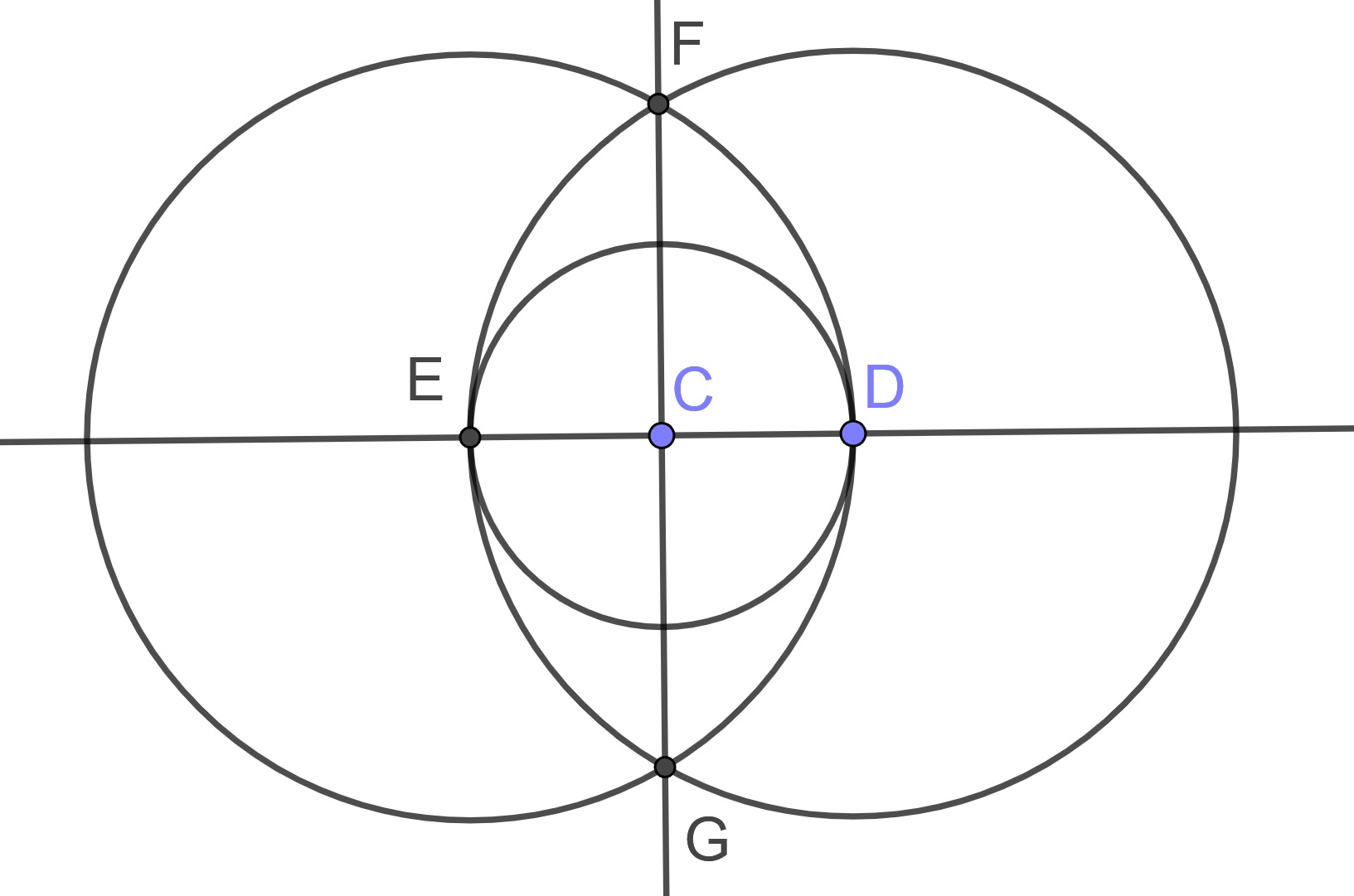
Proposition 10.12 (Euclid's Proposition 12) To a given infinite straight line, from a given point which is not on it, to draw a perpendicular straight line.
The proof of this proposition uses the information from the following diagram.
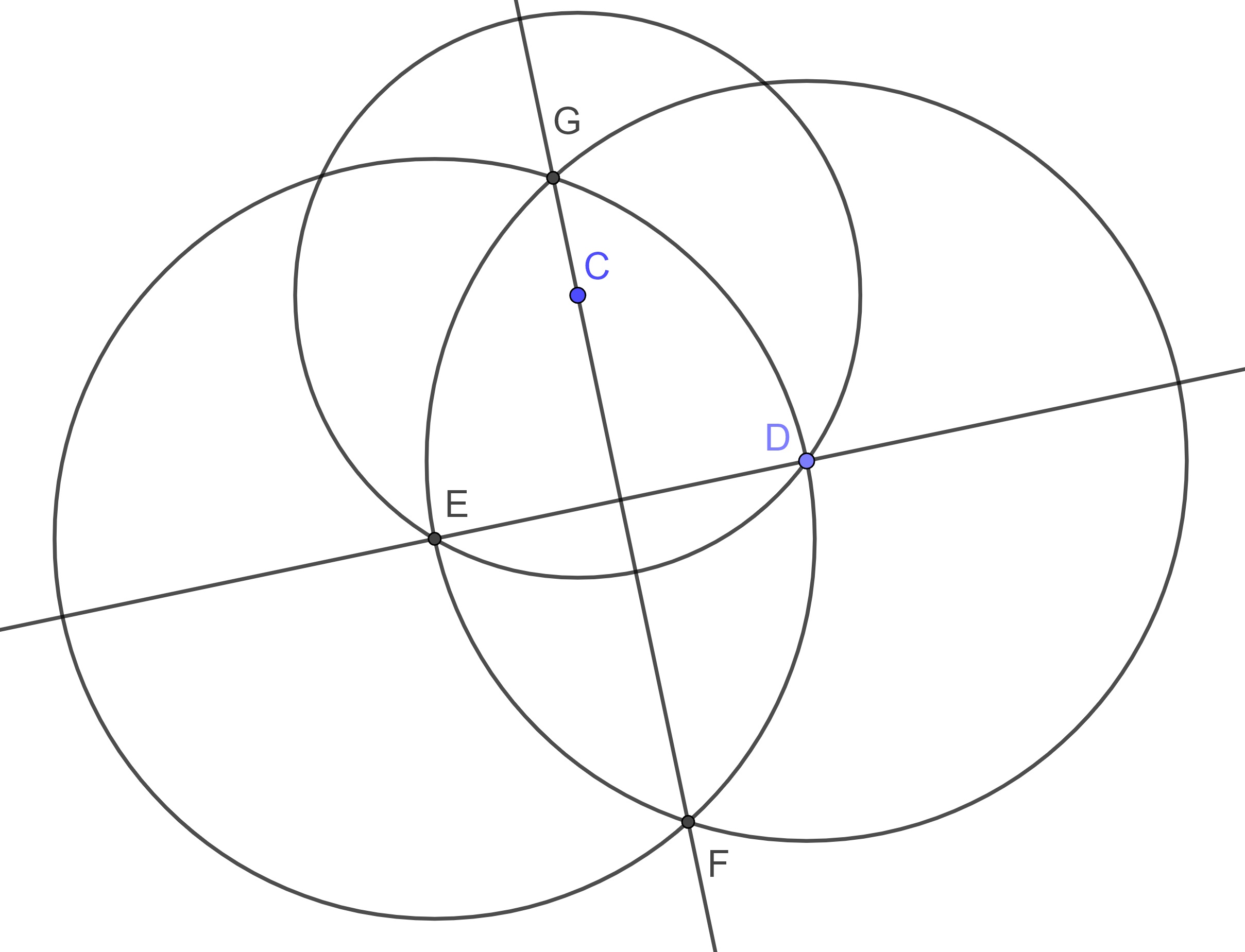
10.3.6 Exercises
Discuss Euclid’s use of the word ‘equal’ in the context of the discussion in Chapter 3.
Write out the details of the proof of Proposition 10.10.
Write out the details of the proof of Proposition 10.11.
Write out the details of the proof of Proposition 10.12.
Complete the following constructions with a physical compass and straightedge, and with a geometry software (using just the straightedge and circles and the more complex construction tools).
- Given a segment of length \(a\), construct a segment of length \(2a\).
- Given a segment of length \(a\) and a segment of length \(b\), construct a segment of length \(a+b\)
- Construct a triangle with side lengths \(a\), \(b\), and \(c\) (with these given).
- Construct a square with side length \(a\).
- Construct a rhombus that is not a square with side length \(a\).