6.2 Pascal’s Triangle and the Binomial Theorem
Pacal’s Triangle is a triangular array where each entry is the sum of the two entries above that location, see Figure 6.1.
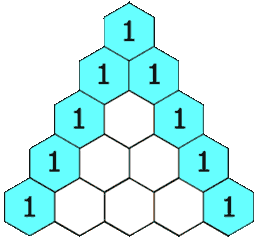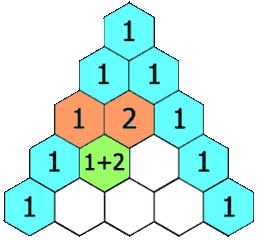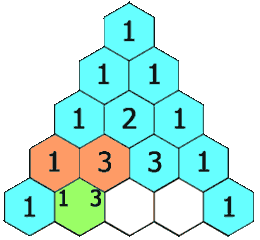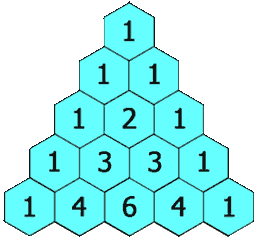
Figure 6.1: Animated Figure of Pascal’s Triangle
While Pascal published this information in 1665 in his Traité du triangle arithmétique, the concept was know in many cultures centuries earlier.
Acharya Pingala demonstrated a knowledge of the key components of \({n \choose k} = {n-1 \choose k} + {n-1 \choose k-1}\) in the 2nd century BC in India. Pascal’s triangle was known in China in the early 11th century through the work of the Chinese mathematician Jia Xian (1010–1070). In the 13th century, Yang Hui (1238–1298) presented the triangle and hence it is still called Yang Hui’s triangle in China.
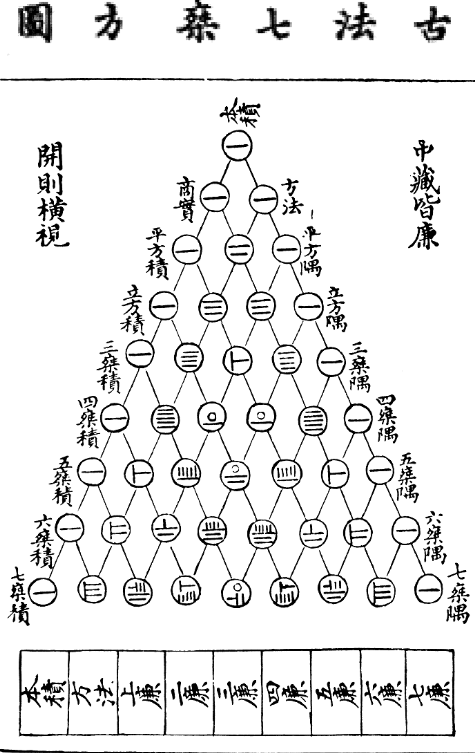
Figure 6.2: Yang Hui’s Triangle
In Iran, this is known as the Khayyam triangle as Omar Khayyám wrote about this triangle in the 11th century in Persia. Even in Europe, the concepts of Pascal’s triangle were known for centuries by Jordanus de Nemore (13th century); Gersonides (14th century); along with Petrus Apianus, Niccolò Fontana Tartaglia, and Gerolamo Cardano (16th century). Pascal took much of this prior work and put it together into a single treatise that connected the concepts to probability theory, causing Abraham de Moivre to name it Pascal’s Triangle in 1730.
We can see the first several rows of Pascal’s triangle below.
\[\begin{array}{lccccccccccccccc} n=0: & & & & & & & & 1 & & & & & & & \\ n=1: & & & & & & & 1 & & 1 & & & & & & \\ n=2: & & & & & & 1 & & 2 & & 1 & & & & & \\ n=3: & & & & & 1 & & 3 & & 3 & & 1 & & & & \\ n=4: & & & & 1 & & 4 & & 6 & & 4 & & 1 & & & \\ n=5: & & & 1 & & 5 & & 10 & & 10 & & 5 & & 1 & & \\ n=6: & & 1 & & 6 & & 15 & & 20 & & 15 & & 6 & & 1 & \\ n=7: & 1& & 7 & & 21 & & 35 & & 35 & & 21 & & 7 & & 1 \\ \end{array}\]
For each \(n\in \mathbb{N}\), we define label the \(n^{\mathrm{th}}\) row and \(k^{\mathrm{th}}\) column as \(\binom{n}{k}\). So we see that for all \(n\) that \[\binom{n}{0} = 1 \quad \mbox{and} \quad \binom{n}{n}=1.\] For \(n>1\) and \(1\leq k \leq n-1\) we define \[\binom{n}{k} = \binom{n-1}{k-1} + \binom{n-1}{k}.\] So Pascal’s Triangle is often written with this notation that we can see below.
\[\begin{array}{lccccccccccccccc} n=0: & & & & & & & & \binom{0}{0} & & & & & & & \\ n=1: & & & & & & & \binom{1}{0} & & \binom{1}{1} & & & & & & \\ n=2: & & & & & & \binom{2}{0} & & \binom{2}{1} & & \binom{2}{2} & & & & & \\ n=3: & & & & & \binom{3}{0} & & \binom{3}{1} & & \binom{3}{2} & & \binom{3}{3} & & & & \\ n=4: & & & & \binom{4}{0} & & \binom{4}{1} & & \binom{4}{2} & & \binom{4}{3} & & \binom{4}{4} & & & \\ n=5: & & & \binom{5}{0} & & \binom{5}{1} & & \binom{5}{2} & & \binom{5}{3} & & \binom{5}{4} & & \binom{5}{5} & & \\ n=6: & & \binom{6}{0} & & \binom{6}{1} & & \binom{6}{2} & & \binom{6}{3} & & \binom{6}{4} & & \binom{6}{5} & & \binom{6}{6} & \\ n=7: & \binom{7}{0} & & \binom{7}{1} & & \binom{7}{2} & & \binom{7}{3} & & \binom{7}{4} & & \binom{7}{5} & & \binom{7}{6} & & \binom{7}{7} \\ \end{array}\]
This notation is very common when we look at combinations and permutations. We often think of \(\binom{n}{k}\) as the number of ways that we can choose \(k\) things out of \(n\) total options. For instance, if we have \(20\) people and we need a committee of \(5\), there are \(\binom{20}{5}\) ways of creating such a committee. We will go into this perspective in more detail in the next section.
6.2.1 Binomial Theorem
An important application of Pascal’s triangle is its relationship to the coefficients of the Binomial Theorem.
Related Content Standards
- (HSA.APR.4) Know and apply the Binomial Theorem for the expansion of \((x+y)^n\) in powers of \(x\) and \(y\) for a positive integer \(n\), where \(x\) and \(y\) are any numbers, with coefficients determined for example by Pascal’s Triangle.
Theorem 6.3 (Binomial Theorem) Let \(a,b\) be in a number system with the distribution property and \(ab=ba\), and let \(n\in \mathbb{N}\), then \[(a+b)^n = \binom{n}{0} a^n b^0 + \binom{n}{1} a^{n-1}b^1 + \cdots + \binom{n}{n-1} a^{1}b^{n-1} + \binom{n}{n} a^0 b^n.\]
We need commutativity of \(a\) and \(b\) so that \(b (a^k b^l) = a^k b^{l+1}\) in the proof below.
Proof. We will prove this using induction on the exponent. So for \(a,b\) and for \(n\in \mathbb{N}\) we let \(P(n)\) be the statement that \[(a+b)^n = \binom{n}{0} a^n b^0 + \binom{n}{1} a^{n-1}b^1 + \cdots + \binom{n}{n-1} a^{1}b^{n-1} + \binom{n}{n} a^0 b^n.\]
We will often compress this statement using summation notation into \[(a+b)^n = \sum_{j=0}^n \binom{n}{j} a^{n-j}b^j\] in order to reduce the amount of writing. Remember that mathematicians are inherently lazy and want to compress as much information into as few symbols as possible.
So, \(P(0)\) is the statement that \((a+b)^0 = 1\), which is defined to be true.
We now move to our induction step.
If we assume that for some integer \(m\) that \(P(m)\) is true, we see that \[\begin{align*} (a+b)^{m+1} = & (a+b) \cdot (a+b)^m\\ = & (a+b) \left( \binom{m}{0} a^m b^0 + \binom{m}{1} a^{m-1}b^1 + \cdots + \binom{m}{m-1} a^{1}b^{m-1} + \binom{m}{m} a^0 b^m\right) \\ = & (a+b) \left( \sum_{j=0}^m \binom{m}{j} a^{m-j} b^j \right) \\ \end{align*}\] We then distribute the summation over \((a+b)\) and get \[\begin{align*} (a+b)^{m+1} = & \left( \sum_{j=0}^m \binom{m}{j} a^{m-j+1} b^j \right) + \left(\sum_{j=0}^m \binom{m}{j} a^{m-j}b^{j+1} \right) \\ \end{align*}\] In order to put these two sums together, we need to reindex the second summation so that the powers of \(a\) and \(b\) are the same. \[\begin{align*} (a+b)^{m+1} = & \left( \sum_{j=0}^m \binom{m}{j} a^{m-j+1} b^j \right) + \left(\sum_{j=1}^{m+1} \binom{m}{j-1} a^{m-j+1}b^{j} \right) \\ \end{align*}\] We then see that the two summations start and end at different points. So we pull the two points that don’t line up off of the summations so that we can add the summations together. \[\begin{align*} (a+b)^{m+1} = & \binom{m}{0} a^{m+1} b^0 + \left( \sum_{j=1}^m \binom{m}{j} a^{m-j+1} b^j \right) \\ & + \left(\sum_{j=1}^{m} \binom{m}{j-1} a^{m-j+1}b^{j} \right) + \binom{m}{m} a^{0}b^{m+1} \\ = & \binom{m}{0} a^{m+1}b^0 + \left( \sum_{j=1}^m \left(\binom{m}{j} + \binom{m}{j-1} \right) a^{(m+1)-j}b^j \right) + \binom{m}{m} a^0 b^{m+1} \\ \end{align*}\] We then use the definition of Pascal’s triangle to combine \(\left(\binom{m}{j} + \binom{m}{j-1} \right)\) into \(\binom{m+1}{j}\) to get \[\begin{align*} (a+b)^{m+1} = & \binom{m}{0} a^{m+1}b^0 + \left( \sum_{j=1}^m \binom{m+1}{j} a^{(m+1)-j}b^j \right) + \binom{m}{m} a^0 b^{m+1} \\ \end{align*}\] Since \(\binom{m}{0}=\binom{m+1}{0}=1\) and \(\binom{m}{m}=\binom{m+1}{m+1}=1\) we can rewrite this as \[\begin{align*} (a+b)^{m+1} = & \binom{m+1}{0} a^{m+1} b^0 + \left( \sum_{j=1}^m \binom{m+1}{j} a^{(m+1)-j}b^j \right) + \binom{m+1}{m+1} a^0 b^{m+1} \\ = & \sum_{j=0}^{m+1} \binom{m+1}{j} a^{(m+1)-j}b^j \end{align*}\] So \(P(m+1)\) is true.
Therefore, by induction, \(P(n)\) is true for all \(n\in \mathbb{N}\).
For the first few values of \(n\) we see that we have the following: \[\begin{array}{lccccccccccccccc} (a+b)^0 = & & & & & & & & 1 & & & & & & & \\ (a+b)^1 = & & & & & & & 1a & + & 1b & & & & & & \\ (a+b)^2 = & & & & & & 1a^2 & + & 2ab & + & 1b^2 & & & & & \\ (a+b)^3 = & & & & & 1a^3 & + & 3a^2b & + & 3ab^2 & + & 1b^3 & & & & \\ (a+b)^4 = & & & & 1a^4 & + & 4a^3b & + & 6a^2b^2 & + & 4ab^3 & + & 1b^4 & & & \\ (a+b)^5 = & & & 1a^5 & + & 5a^4b & + & 10a^3b^2 & + & 10a^2b^3 & + & 5ab^4 & + & 1b^5 & & \\ \end{array}\]
While the connection between the binomial theorem and Pascal’s triangle is very useful, it would be very helpful to have a compressed formula for \(\binom{n}{k}\) so that we don’t have to write out all of the previous rows to find its value. We will find this formula in the next section.
6.2.2 Exercises
Use the Binomial theorem to expand the following.
- \((x-2y)^5\)
- \((1+2i)^6\)
- \((-3x+5y)^8\)
- \(\left(x-\frac{1}{x}\right)^4\)
Use the Binomial theorem to expand \((x+y+z)^3\) by first expanding \(\left( (x+y) + z\right)^3\) and then expanding the \((x+y)^j\) terms. Can you find a generalization for \((x+y+z)^n\)?