11.4 Distance

We will now move to a generalization of the concept of length using a more rigorous mathematical definition.

Definition 11.1 A metric, or distance, on a set \(X\) is a function \[d: X\times X \rightarrow [0,\infty)\] such that for all \(x,y,z\in X\) the following three axioms are satisfied:

  • (D1.) \(d(x,y)=0 \Leftrightarrow x=y\) (identity of indiscernibles)
  • (D2.) \(d(x,y)=d(y,x)\) (symmetry)
  • (D3.) \(d(x,y) \leq d(x,z)+d(z,y)\) (triangle inequality).

If we have equality in the triangle inequality, \(d(x,y)=d(x,z)+d(z,y)\), we say that \(x\),\(y\), and \(z\) are colinear and \(z\) is between \(x\) and \(y\).

If \(X\) is our standard plane, \(\mathbb{R}^2\), the function \(d_2:\mathbb{R}^2\times \mathbb{R}^2 \rightarrow [0,\infty)\) defined by \[d_2\left( (x_1,y_1), (x_2,y_2)\right) = \sqrt{ (x_2-x_1)^2 + (y_2-y_1)^2}\] satisfies these axioms and is called the Euclidean distance on the plane because it corresponds with the geometry of Euclid’s Elements.

An alternate distance on the plane can be given by \(d_1:\mathbb{R}^2 \times \mathbb{R}^2 \rightarrow [0,\infty)\) defined by \[d_1\left( (x_1,y_1), (x_2,y_2)\right) = |x_2-x_1| + |y_2-y_1|\] and is often called the taxicab distance as it measures the distance traveled along a grid. Hermann Minkowski used this distance in his exploration of non-Euclidean geometries in his study of relativity in the late 1800s.

Unlike the Euclidean distance, the taxicab distance allows multiple paths between two points that have minimal length. We can see below that the distance between the points \((0,0)\) and \((2,2)\) is \(4\), and that both paths given have this minimal length.

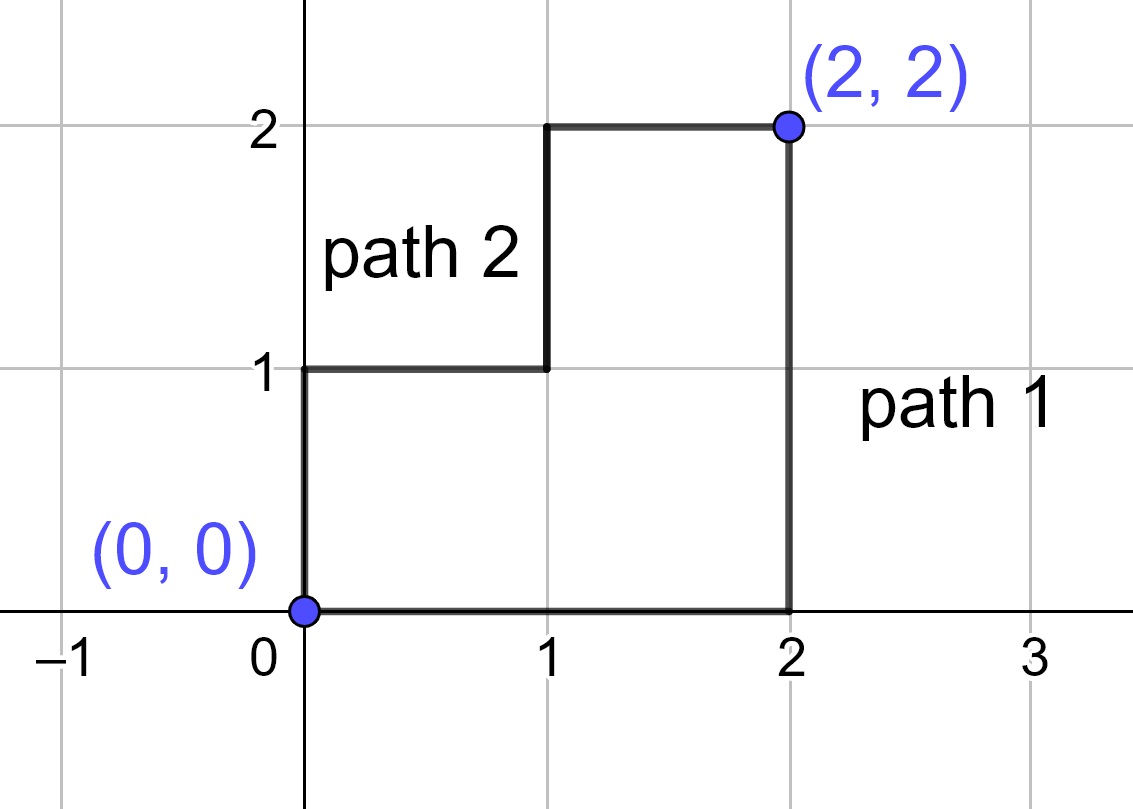
However, any point, \(C\), on the line segment connecting two points, \(A\) and \(B\), can be considered between \(A\) and \(B\) since \(d(A,C)+d(C,B) = d(A,B)\) for every point on the line segment. This means that the lines in Euclidean geometry and the lines in the taxicab geometry are the same but do not have all of the same properties.

A third distance that has a very natural derivation is \(d_\infty: \mathbb{R}^2\times \mathbb{R}^2 \rightarrow [0,\infty)\) defined by \[d_\infty \left( (x_1,y_1), (x_2,y_2)\right) = \mbox{max } (|x_2-x_1|,|y_2-y_1|) \] and is often called the Chebyshev distance after Pafnuty Chebyshev who was the first to systematically study the distance in the mid 1800s.

11.4.1 Circles and Lines

One way that we can see the difference between these three metrics is to look at the circles created by the metrics.

Definition 11.2 Let \(X\) be a set with a distance \(d\). A circle centered at a point \(c\in X\) with radius \(r\) is \[C_{(c,r)} = \left\{ x\in X \: \vert \: d(x,c)=r\right\}.\]

Since a circle is defined as the set of points equidistant from a fixed point, we see that circles are defined by the distance. Hence, when we look at the circles that correspond to the three distances described above, we have different sets of points.

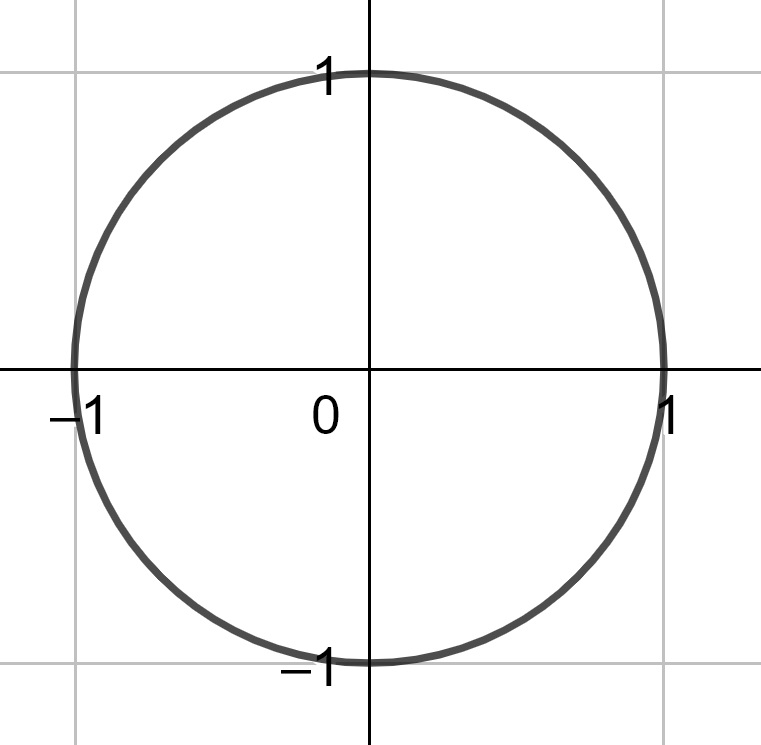
Unit Circle for the Euclidean Distance

Figure 11.1: Unit Circle for the Euclidean Distance

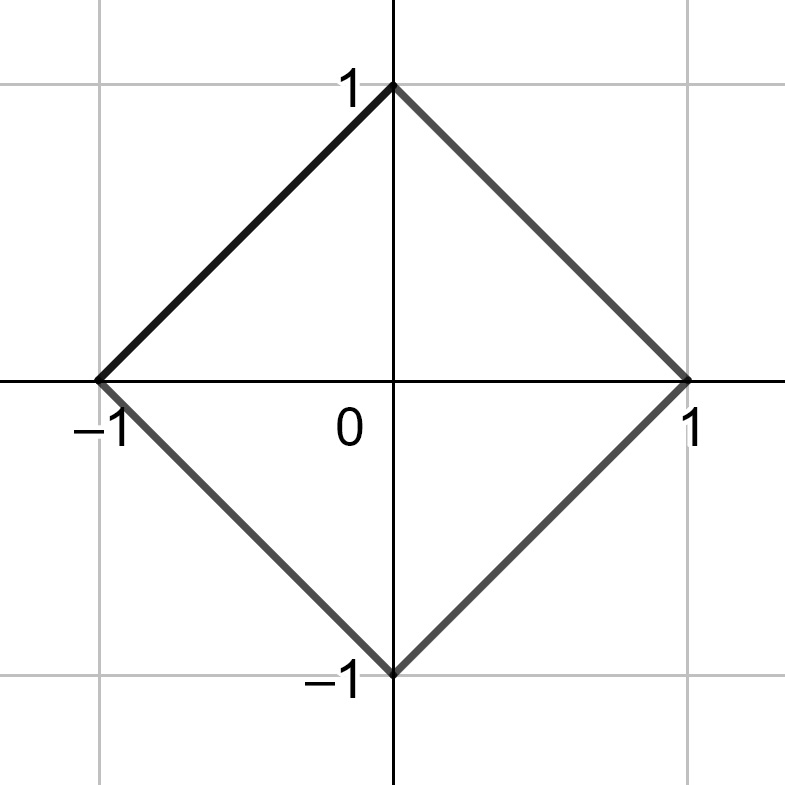
Unit Circle for the Taxi Cab Distance

Figure 11.2: Unit Circle for the Taxi Cab Distance

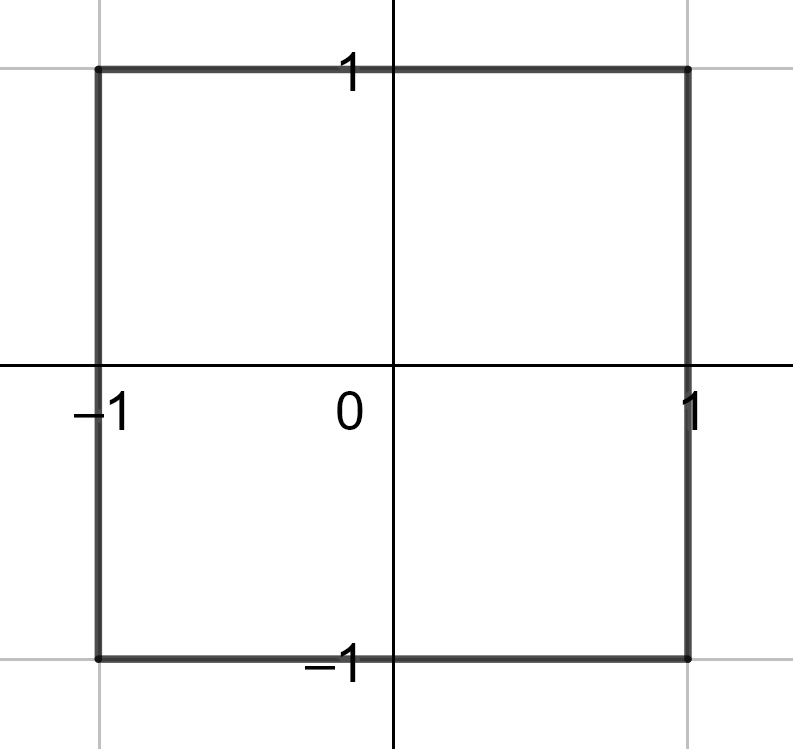
Unit Circle for the Chebechev Distance

Figure 11.3: Unit Circle for the Chebechev Distance

We also see that lines in the plane are also defined by the distance.

Definition 11.3 Let \(d\) be a distance defined on \(\mathbb{R}^2\). A line in \(\mathbb{R}^2\) is the set of points equidistant from two distinct fixed points, \[l_{(x,y)} = \left\{ z\in \mathbb{R}^2 \: \vert \: d(z,x)=d(z,y)\right\}.\]

For each of the distances on \(\mathbb{R}^2\) defined above, the lines are the same.

11.4.2 Related Horizon Content Knowledge

This concept of a metric, or distance, extends beyond the two-dimensional plane. If we look at the real numbers, \(\mathbb{R}\), we have the standard metric of \(d(x,y)=|x-y|\). We could also define a distance on \(\mathbb{R}\) using \[d_3(x,y) = \frac{|x-y|}{1+|x-y|}.\]

We can also extend the idea of metrics to other sets. If \(X\) is a non-empty set the function \(d_0:X\times X \rightarrow \{0,1\}\) defined by \[d_0(x,y)=\begin{cases} 0 & x=y \\ 1 & x\neq y \\ \end{cases}\] is called the discrete metric. If we let \(C([0,1])\) be the continuous real-valued functions on the closed interval \([0,1]\), we can define a metric on this set as \[d(f,g) = \mbox{max} \{ f(x)-g(x) \: \vert \: x\in [0,1]\}.\]

11.4.3 Exercises

  1. Is length (discussed in Section 11.1) different than distance? Explain your answer.

  2. Prove that \[d_3(x,y) = \frac{|x-y|}{1+|x-y|}\] satisfies the properties for a metric on \(\mathbb{R}\).

  3. Verify using circles that the lines determined by the two points are the same for Euclidean, Taxicab, and Chebyshev distances.

  4. Often distances are given with a direction (e.g., travel three miles due east). For Euclidean distance, find three different ways to give direction.

  5. Prove that \[d(x,y)= \left\{ \begin{array}{l} 0 \quad \mbox{if} \quad x=y \\ 1 \quad \mbox{if} \quad x\neq y\\ \end{array} \right.\] is a metric on the set of real numbers.

  6. Prove that for the set of \(2\times 2\) matrices with real coefficients, \[d(A,B)=\mbox{rank} (B-A)\] is a metric on the set.

  7. Using Euclidean distance, find the length of the shortest path from \((-1,7)\) to the \(x\)-axis and up to \((8,5)\).