13.4 Rotations

If we represent the plane by a piece of paper, the rotations correspond to holding down a point on the paper and rotating the paper around that point. This means that as long as your rotation is not a multiple of \(2\pi\), the only fixed point of the plane is the center of the rotation. Intuitively we can see that this transformation of the plane does not change the paper is any way and so is an isometry of the plane.

13.4.1 Synthetic Plane

Definition 13.14 Given a point \(C\) and an angle \(\theta\), we define the rotation about \(C\) by \(\theta\) for every point \(A\) in the plane by \(A'=R_{(C,\theta)}(A)\) is the unique point in the plane so that \(\overline{CA}\) is the same length as \(\overline{CA'}\) and the measure of angle \(\angle ACA'\) equals \(\theta\).

If we let \(C\) and \(\alpha\) be given so that \(R_{(C,\alpha)}\) is a rotation, for any two points \(A\) and \(B\), we can let \(A'=R_{(C,\alpha)}(A)\) and \(B'=R_{(C,\alpha)}(B)\). If \(A\), \(B\), and \(C\) are not co-linear, we can show that triangles \(\triangle CAB\) and \(\triangle CA'B'\) have equal sides and angles.

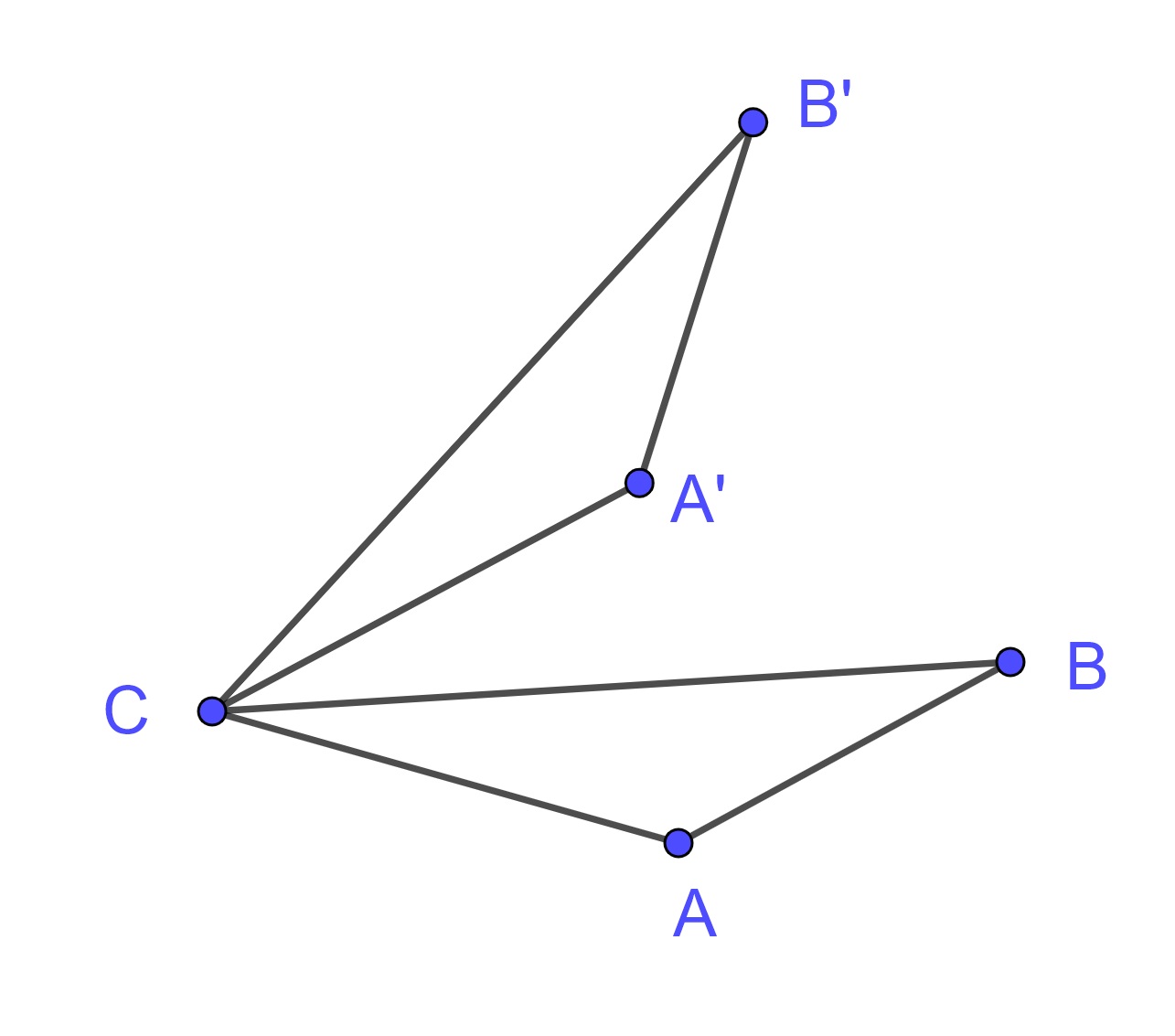
From the definition of a rotation, we know that \(\overline{CA}\) and \(\overline{CA'}\) have the same length, and \(\overline{CB}\) and \(\overline{CB'}\) have the same length. Similarly angles \(\angle ACA'\) and \(\angle BCB'\) are equal. From this, we can see that angles \(\angle ACB\) and \(\angle A'CB'\) are equal. So by the SAS theorem, we have that \(\overline{AB}\) and \(\overline{A'B'}\) have the same length.

If \(A\), \(B\), and \(C\) are co-linear, one can use properties of line segments to prove that \(\overline{AB}\) is equal to \(\overline{A'B'}\).

13.4.2 Complex Plane

If \(z=re^{i\alpha}\), we can see that \(re^{i(\alpha+\theta)}= r e^{i\alpha} e^{i\theta} = e^{i\theta} z\) is the rotation around the origin of \(z\). We can then provide notation for these rotations as \[R_{(0,\theta)}(z) = e^{i\theta} \cdot z.\]

If we have a point \(c\in \mathbb{C}\) and an angle \(\theta\) we can construct the rotation about \(c\) of angle \(\theta\) through a composition of translations and the rotation about the origin. We begin the process by translating the point \(c\) to the origin. We can then rotate around the origin by \(\theta\) and then translate the origin back to \(c\). So the rotation about \(c\) by an angle \(\theta\) is given by \[T_c \circ R_{(0,\theta)} \circ T_{-c}.\]

Definition 13.15 Given an angle \(\theta\), we define the rotation about a complex number \(c\) as \[R_{(c,\theta)}(z) = e^{i\theta} \cdot (z-c)+c.\]

Since \[R_{(c,\theta)}(z) = e^{i\theta} \cdot (z-c)+c = e^{i \theta} z + \left(1-e^{i\theta}\right)c,\] we can see that \(R_{(c,\theta)}(z)\) is a complex function of the form \(f(z)=az+b\) with \(|a|=1\) and if the angle of rotation is not an integer multiple of \(2\pi\), \(a\neq 1\). The following theorem shows that these functions are equivalent.

Theorem 13.11 Let \(f:\mathbb{C}\rightarrow \mathbb{C}\) be a function. Then \(f\) is a rotation if and only if \(f(z)=az+b\) for some \(a\in \mathbb{C}\setminus \{1\}\) with \(|a|=1\) and for some \(b\in \mathbb{C}\), or for \(a=1\) and \(b=0\).

Proof. If \(f(z)=az+b\) with \(|a|=1\) we can discover information about \(f\) by looking at its fixed points, the points \(c\in \mathbb{Z}\) such that \(f(c)=c\). We can then see that the fixed point of \(f\) corresponds to the points where \(ac+b=c\), or when \[c= \frac{b}{1-a}.\] So if \(a\neq 1\), there is a single fixed point and we can see that \[f(z)= a \left( z-\frac{b}{1-a}\right) + \frac{b}{1-a}\] and that \(f\) is a rotation. If \(a=1\) and \(b=0\), we see that we have the identity, which can be considered a rotation of angle \(0\) about any point.

If \(f\) is a rotation, then \[f(z) = e^{i\theta} (z-c)+c = e^{i\theta} z + c-ce^{i\theta} = az+b,\] where \(a=e^{i\theta}\), so \(|a|=1\) and \(b= c-ce^{i\theta}\). If \(a=1\), then \(f(z)=z\) and so \(b=0\).

13.4.3 Cartesian Plane and Vector Space

Now that we know the representations of rotations from the perspective of the complex plane we can use that information to find the representations for rotations from the other perspectives.

If we let \(z=x+iy\), we can see that \[R_{(0,\theta)}(z) = (\cos(\theta) + i \sin(\theta)) (x+iy) = \left(x\cos(\theta) - y \sin(\theta)\right) + i \left(x\sin(\theta) + y \cos(\theta) \right).\]

So in the Cartesian plane perspective, the rotation about the origin by angle \(\theta\) can be written as \[R_{\left((0,0),\theta\right)}\left((x,y)\right)= \left( x \cos(\theta)-y\sin(\theta), x\sin(\theta)+y\cos(\theta)\right).\]

In the perspective of the vector space we have \[R_{\langle 0,0\rangle, \theta} \left( \langle x,y\rangle \right) = \begin{pmatrix} \cos(\theta) & -\sin(\theta) \\ \sin(\theta) & \cos(\theta) \end{pmatrix} \begin{pmatrix} x \\ y \end{pmatrix} .\]

The algebraic representations for the general rotations can be found using similar methods as used in the complex plane perspective.

Related Content Standards

• (HSG.GPE.5) Prove the slope criteria for parallel and perpendicular lines and use them to solve geometric problems (e.g., find the equation of a line parallel or perpendicular to a given line that passes through a given point).

For the rotation by \(\frac{\pi}{2}\) about a point \((h,k)\) can then be written as \[R_{((h,k),\frac{\pi}{2})}\begin{pmatrix} x \\ y \end{pmatrix} = \begin{pmatrix} 0 & -1 \\ 1 & 0 \end{pmatrix} \begin{pmatrix} x-h \\ y-k \end{pmatrix} + \begin{pmatrix} h \\ k \end{pmatrix} = \begin{pmatrix} -y+k+h \\ x-h+k \end{pmatrix}\]

If we apply this rotation to the line \(y=m(x-h)+k\), we have \[R_{((h,k),\frac{\pi}{2})} \begin{pmatrix} x \\ m(x-h)+k \end{pmatrix} = \begin{pmatrix} -(m(x-h)+k)+k+h \\ x-h+k \end{pmatrix}= \begin{pmatrix} -m(x-h)+h \\ x-h+k \end{pmatrix}\] and since \[\frac{-1}{m} \left( (-m(x-h)+h)-h\right)+k = x-h+k\] we see that the image of the line under the rotation is \(y=\frac{-1}{m} (x-h)+k\). So the slope of perpendicular lines are negative multiplicative reciprocals of each other.

13.4.4 Compositions and Groups of Rotations

If we have two rotations centered at the same point \(c\), \(R_{(c,\theta)}\) and \(R_{(c,\phi)}\), we see that the composition \[R_{(c,\theta)} \circ R_{(c,\phi)} (z) = e^{i\theta} \left( \left( e^{i \phi} (z-c) + c\right) -c\right) + c = e^{i(\theta+\phi)} (z-c)+c\] is a rotation centered at \(c\) with the new angle of rotation the sum of the original two angles, \[R_{(c,\theta)} \circ R_{(c,\phi)} = R_{(c, \theta+\phi)}.\] Hence with the same center, compositions of rotations is closed under composition. Since \(R_{(c,0)}(z)=z\) and \(R_{(c,\theta)}^{-1} = R_{(c,-\theta)}\) we see that the set of rotations about a single fixed point forms a group under function composition. For each point \(c\in \mathbb{C}\), we can let \(R_c\) be the set of rotations centered at \(c\).

Theorem 13.12 For each complex number \(c\in \mathbb{C}\), the set of rotations centered at \(c\) with the operation of composition, \((R_c,\circ)\), is a group.

Since the addition of the angles is commutative, the order of operations of the compositions of these two rotations does not matter. Thus the group \((R_c,\circ)\) is abelian.

Since \(R_{(c,\theta)} \circ R_{(c,\psi)} = R_{(c, \theta+\psi)}\), our first instinct is that the composition of rotations about a single center corresponds with the addition of real numbers. However, because of the periodicity of the trigonometric functions, for any angle \(\theta\), we see that \(R_{(c,\theta)} = R_{(c,\theta+2k\pi)}\) for any integer \(k\). We can instead let \[S^1= \left\{ z\in \mathbb{C} \: \vert \: |z|=1\right\}\] be the unit circle in the complex plane. We also know that \(S^1\) can be expressed using angles as \[S^1=\left\{ e^{i\theta} \: \vert \: \theta\in \mathbb{R}\right\}\] with \(e^{i\theta} \cdot e^{i\psi} = e^{i (\theta+\psi)}\). Therefore, \((S^1,\cdot)\) forms a group with identity \(e^{i0}=1\) and inverses \(\left(e^{i\theta}\right)^{-1} = e^{i (-\theta)}\). It is then straight forward to see that this group is isomorphic to \((R_c,\circ)\) with isomorphism \(\phi:S^1\rightarrow R_c\) defined by \[\phi \left(e^{i\theta} \right) = R_{(c,\theta)}.\]

Theorem 13.13 For each complex number \(c\in \mathbb{C}\), the group \((R_c,\circ)\) is isomorphic to the unit circle in \(\mathbb{C}\), \(S^1\), with the operation of multiplication, \((S^1,\cdot)\).

If we look at the composition of two rotations about two different centers we have that

\[\begin{align*} R_{(c,\theta)} \circ R_{(d,\psi)}(z) & = e^{i\theta} \left( e^{i\psi}(z-d)+d-c\right) +c \\ & = e^{i(\theta + \psi)} z + \left( e^{i\theta} \left(1-e^{i\psi}\right) d + (1-e^{i\theta}) c\right) \end{align*}\] If \(\theta+\psi\) is an integer multiple of \(2\pi\), we see that \(e^{i(\theta+\psi)}=1\). So \[R_{(c,\theta)} \circ R_{(d,\psi)}(z) = z + (e^{i\theta}-1) d + (1-e^{i\theta}) c = z+ (e^{i\theta}-1)(d-c).\] Therefore, the composition of the two rotations is a translation. We note that this means that the set of all rotations is not closed under function composition and so does not form a group.

If \(\theta+\psi\) is not an integer multiple of \(2\pi\) we can see that the composition of the two rotations is a function of the form \(f(z)=az+b\) with \(a=e^{i(\theta+\psi)}\). The earlier work on rotations shows that this is a rotation centered at \[\frac{b}{1-a} = \frac{e^{i\theta} \left(1-e^{i\psi}\right) d + (1-e^{i\theta}) c}{1-e^{i(\theta+\psi)}}.\]

Combining the translations and rotations into a single set, we see that we have another subgroup of \(I\).

Definition 13.16 Let \(P\) be the set of orientation preserving isometries of the plane. \[P = \left\{ f: \mathbb{C} \rightarrow \mathbb{C} \: \vert \: f(z)=a z+b \mbox{ for some } a, b \in \mathbb{C} \mbox{ with } |a|=1 \right\}\]

Theorem 13.14 The set of orientation preserving isometries, \(P\), is a subgroup of the isometries, \(I\).

13.4.5 Exercises

1. Express the rotation \(R_{(A,\frac{\pi}{2})}\), where \(A=(0,1)\), as a transformation in each of the different perspectives.

2. Let \(R\) be the rotation about the point \((1,1)\) with an angle of \(\frac{\pi}{3}\).

   1. Write an algebraic representation for the rotation from each of the four perspectives.
   2. Find the image of the circle \(C=\left\{ (x,y)\in \mathbb{R}^2 \: \vert \: (x-2)^2+(y+3)^2 =9\right\}\) under this rotation.
   3. Let \(A=(1,2)\), \(B=(-2,3)\) and \(C=(0,0)\). Find the image of the triangle \(\triangle ABC\) under this rotation.

3. Prove that the set of all rotations of the plane with the operation of composition is not a group.

4. Show that the order of composition matters when composing a rotation and a translation.

5. Let \(f\) and \(g\) be two rotations such that \(g\circ f\) is a translation.

   1. If \(f(z)=a(z-c)+c\) and \(g(z)=b(z-d)+d\), what relationships exist between the coefficients of \(f\) and \(g\)?
   2. What relationships exist between \(f\circ g\) and \(g\circ f\)?

6. Consider the group of orientation preserving isometries, \(P\), in relation to the group of isometries, \(I\). Is \(P\) a normal subgroup of \(I\)? If so, describe the elements of the factor group and determine if the factor group is isomorphic to another known group.

7. Let \(c\in \mathbb{C}\) be a fixed point on the plane. Since the set of rotations about \(c\) form a group, \(R_c\) is a subgroup of \(I\) and \(P\).

   1. Is \(R_c\) a normal subgroup of \(I\)? If so, describe the elements of the factor group and determine if the factor group is isomorphic to another known group.
   2. Is \(R_c\) a normal subgroup of \(P\)? If so, describe the elements of the factor group and determine if the factor group is isomorphic to another known group.

8. Is \(T\), the subgroup of translations a normal subgroup of \(P\)? If so, describe the elements of the factor group and determine if the factor group is isomorphic to another known group.