3.2 Equality and Equivalence in the K-12 Curriculum
We can see from the discussion in the previous two sections that the concept of two things being equivalent mathematically is a very difficult and abstract concept. It is no surprise then that students of all grade levels have many different conceptions and misconceptions revolving around this concept of equality and equivalence.
Since all of the number systems that arise in the elementary and early secondary curriculum have an inherent order described by the \(\leq\) and \(<\) symbols, the concept of equality is often described in terms of a balanced scale. Another conception around the equal sign is that two sets of objects have the same number of items, determined by counting the number of objects. This is likely since the concept of equality arises in the first grade where students are only working with whole numbers.
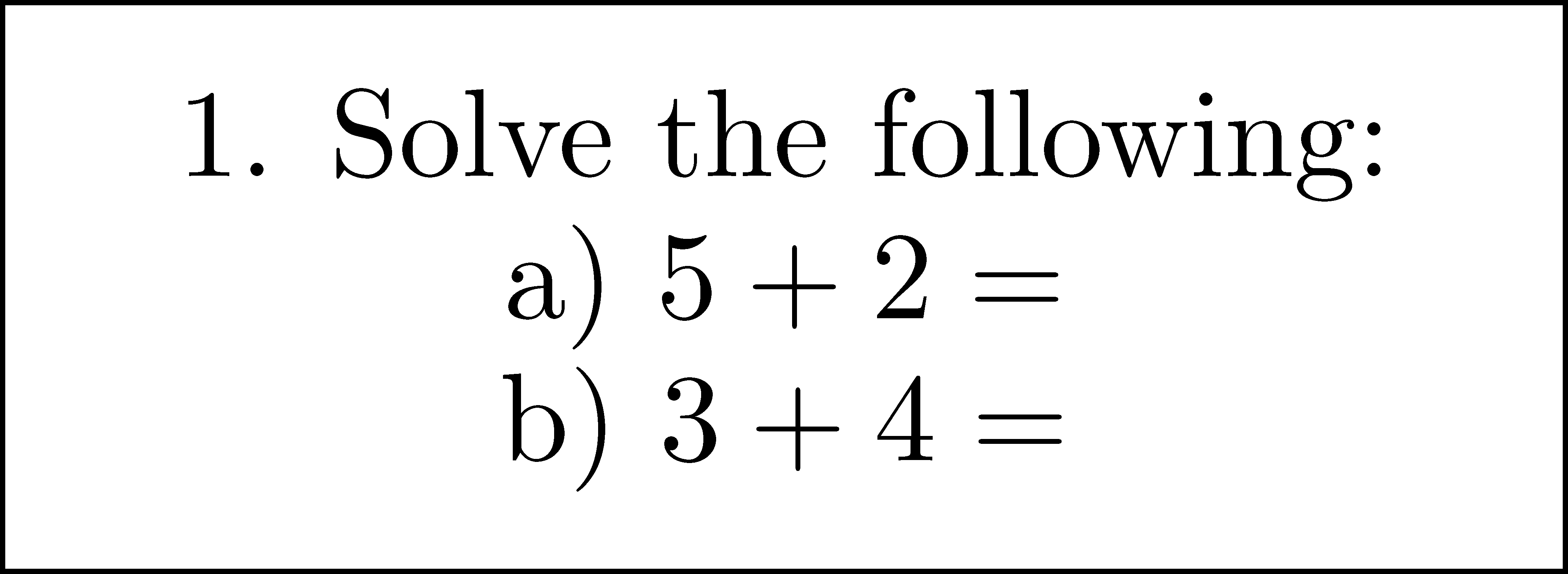
Figure 3.3: Sample problems
One of the common misconceptions surrounding the equal sign is that the symbol implies an action of doing some type of computation. For instance, students usually see the equal sign in the context of the type of problems seen in Figure 3.3.
These type of problems promote an operational understanding of the equal sign, rather than a relational or substitutional understanding that is essential for later work (Gilmore et al., 2018, pp. 145–150). Because secondary mathematics students maintain many misconceptions about the concept of equality and the meaning of the equal sign, we will take some time to reflect on some key content standards from first grade that have a very strong influence on student success of learning mathematics in the middle school.
Related Content Standards
- (1.OA.7) Understand the meaning of the equal sign, and determine if equations involving addition and subtraction are true or false. For example, which of the following equations are true and which are false? \(6 = 6\), \(7 = 8 - 1\), \(5 + 2 = 2 + 5\), \(4 + 1 = 5 + 2\).
- (1.OA.8) Determine the unknown whole number in an addition or subtraction equation relating three whole numbers. For example, determine the unknown number that makes the equation true in each of the equations \(8 + ? = 11\), \(5 = ? - 3\), \(6 + 6 = ?\).
Figure 3.4: Pan balances
We should notice that in standard (1.OA.D.8) that the unknown should not always be at the end of a string of mathematical symbols and is based on educational research that compares students from different cultures and their understanding of the equal sign (Gilmore et al., 2018, pp. 148–150). Instead it should be at many different locations in order to make sure that students do not internalize the misconception that the equal sign means to compute. They should instead develop the concept of the equal sign representing two things that have the same value in some way. It is this understanding of two things looking different but representing the same underlying value that causes the equal sign to represent an equivalence.
Another method that may possibly contribute to a more relational understanding of the equal sign is the introduction of the equal sign alongside the greater than (\(>\)) and less than (\(<\)) symbols to emphasize the role of the equal sign in the comparison of the size of numbers. This comparison concept can be further reinforced with a pan balance (See Figure 3.4).
This concept of a pan-balance can give students a concrete idea to attach to the meaning of the equal and inequality signs. However, like all good analogies, the pan balance is challenging to use with negative numbers and breaks down if you are comparing numbers in an unordered number system such as the complex numbers.
3.2.1 Exercises
A student is given the following task.
Sophia goes to the store with \(\$5.00\) and buys two packs of gum for \(\$1.20\). She then gives \(\$2.00\) to her friend to buy a drink. How much money does she have left?
The student then writes the following on their paper. \[5.00-1.20=3.80-2.00=1.80, \mbox{ so Sophia has } \$1.80 \mbox{ left.}\]
What ideas from this section regarding the equal sign and equivalence would you use to provide feedback to this student?
What are other points of feedback that you would provide to this student?
A student asks you what the equal sign means in the context of \(\frac{1}{2}=\frac{2}{4}\) since those symbols are not the same. How would you respond to this student? How would it change depending on the grade level of the student?
What are the meanings of the equal signs in the task?
Evaluate the function \(f(x)=3x-4\) for \(x=2\).