13.8 Dilations and Similarity
Related Content Standards
- (7.G.1) Solve problems involving scale drawings of geometric figures, including computing actual lengths and areas from a scale drawing and reproducing a scale drawing at a different scale.
- (8.G.3) Describe the effect of dilations, translations, rotations, and reflections on two-dimensional figures using coordinates.
- (8.G.4) Understand that a two-dimensional figure is similar to another if the second can be obtained from the first by a sequence of rotations, reflections, translations, and dilations; given two similar two-dimensional figures, describe a sequence that exhibits the similarity between them.
- (HSG.SRT.2) Given two figures, use the definition of similarity in terms of similarity transformations to decide if they are similar; explain using similarity transformations the meaning of similarity for triangles as the equality of all corresponding pairs of angles and the proportionality of all corresponding pairs of sides.
13.8.6 Exercises
Shane is working with transformations of an arrow shape about line \(l\) and point \(P\).
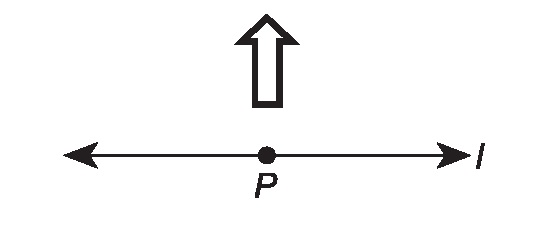
Draw the image of the arrow after 2 successive transformations: a reflection across \(l\) and then a rotation of \(270^\circ\) clockwise around \(P\). Show the image after each transformation.
Draw a dilation of the original arrow centered at \(P\) with a scale factor of 3. Show your work, and explain how you found your answer.
How does the area of the arrow after the dilation in Part b) compare to the area of the original arrow? Explain your answer.
For each function below, identify whether \(f(z)\) is a size transformation or isometry.
- If it is an isometry, identify what type of isometry it is and describe as much detail as possible (e.g., if it is a rotation, give the center and angle of rotation).
- If it is a similarity transformation, identify the scalar of the size transformation.
- \({\displaystyle f(z)= -3z+2 }\)
- \({\displaystyle f(z)= (2+2\sqrt{3}i)z - (3+i)}\)
- \({\displaystyle f(z)= (-1+\sqrt{3}i)\overline{z} + (2-i)}\)
- \({\displaystyle f(z)= \left(-\frac{1}{3}i\right)z}\)
- \({\displaystyle f(z)=\left( \frac{3}{5}+\frac{4}{5}i\right) \overline{z} + 8 -16i}\)
- \({\displaystyle f(z)= z+2-2i}\)
- \({\displaystyle f(z)=\sqrt{3} \overline{z} -i}\) a \({\displaystyle f(z)=\left(-\frac{\sqrt{2}}{2}+\frac{\sqrt{2}}{2}i\right) (z-2+3i) + 2-3i }\)
- \({\displaystyle f(z)=i \overline{z} + (-2+2i)}\)
- \({\displaystyle f(z)=\left(\frac{1}{2}+i\right)z}\)
- The composition of three reflections over three distinct lines intersecting at a single point.
- The composition of two reflections over two distinct intersecting lines.
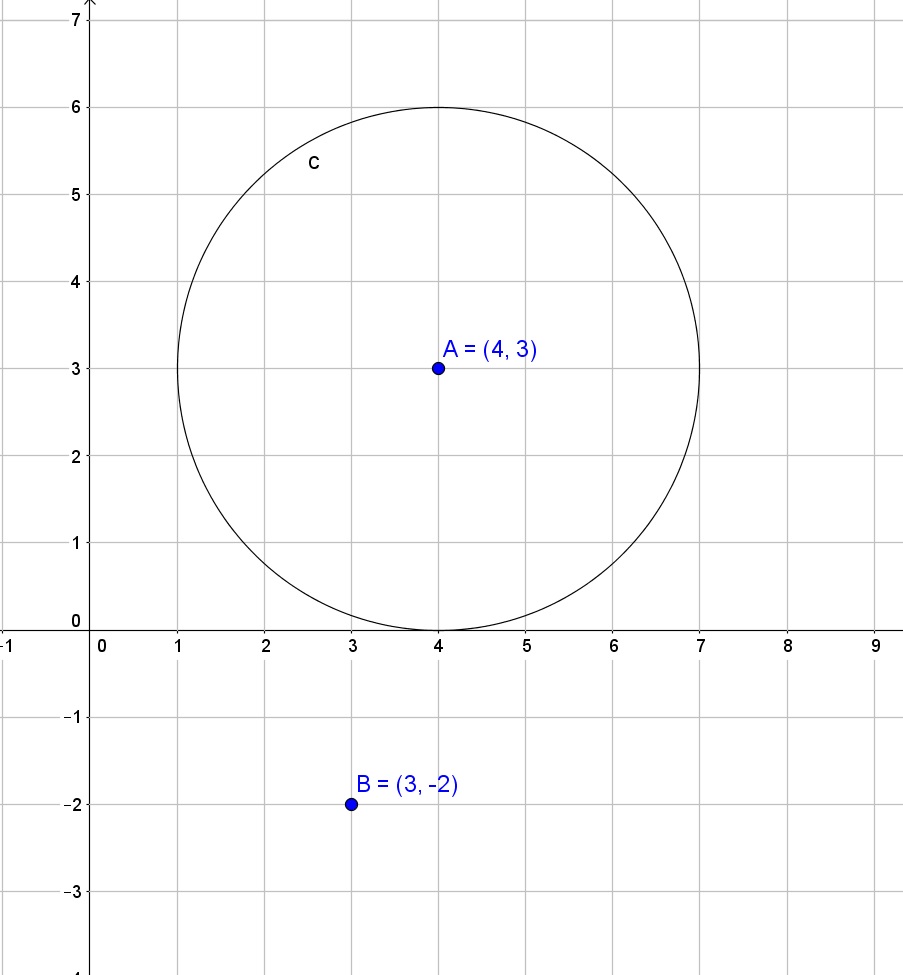
Draw the image of the circle, \(c\), and find the equation of the image, after a dilation centered at \(B\) with ratio of similitude of \(0.5\).