8.1 Properties of the Ring of the Integers

In this section we spend time better understanding the integral domain of the integers. We will look at some of the divisibility properties that are the underpinnings for our standard long division algorithms and build up to the prime factorization of the integers.

The first key component of the integers that we will look at is the Division Algorithm that we first stated and proved in Section 6.

Theorem 8.1 (The Division Algorithm for Integers) If $a$ and $b$ are integers with $b>0$, then there are unique integers $q$ and $r$ such that \[a=bq+r, \quad \mbox{with } 0\leq r <b.\]

We call the integer $q$ in the division algorithm the quotient of $a$ and $b$ and we call $r$ the remainder of the quotient of $a$ and $b$.

Related Content Standards

(4.NBT.6) Find whole-number quotients and remainders with up to four-digit dividends and one-digit divisors, using strategies based on place value, the properties of operations, and/or the relationship between multiplication and division. Illustrate and explain the calculation by using equations, rectangular arrays, and/or area models.
(5.NBT.6) Find whole-number quotients of whole numbers with up to four-digit dividends and two-digit divisors, using strategies based on place value, the properties of operations, and/or the relationship between multiplication and division. Illustrate and explain the calculation by using equations, rectangular arrays, and/or area models.

Proof. Let $a$ and $b$ be integers with $b>0$. We will first prove the existence of integers $q$ and $r$ such that \[a=bq+r, \quad \mbox{with } 0\leq r <b\] and then prove that these integers are unique.

Existence. If $a\geq 0$, then we can let \[S= \left\{ a-kb \vert \: a-kb\geq 0 \mbox{ and $k$ is a non-negative integer}\right\}.\] Since $a\geq 0$, we see that $a=a-0\cdot b$ is an element of $S$ and so $S$ is non-empty. We also see that $S \subseteq [0,a]$.

So by the Well-Ordering Property of the Integers, there is a smallest element of $S$ which we will call $r$. Since $r\in S$, there exists a non-negative integer $q$ such that $r=a-qb$.

Since $r$ is the smallest element of $S$ and since $a-(q+1)b<a-qb=r$, we see that $a-(q+1)b<0$, otherwise it would be a smaller element of $S$.

This implies that $r=a-qb<b$. Therefore we have the existence of the $q$ and $r$.

If $a<0$, using the above process, we can find non-negative integers $q$ and $r$, with $0\leq r<b$, such that $-a=bq+r$. So $a=b(-q)+r$ satisfies the existence statement.
Uniqueness. In order to prove the uniqueness of the quotient and remainder, we assume that there are two pairs of integers $(q_1,r_1)$ and $(q_2,r_2)$ such that \[a= b q_1 + r_1 \mbox{ and } a= b q_2 + r_2, \mbox{ with } 0\leq r_1<b \mbox{ and } 0\leq r_2 <b.\] This implies that $b q_1 + r_1 = b q_2 + r_2$ and by rearranging the terms we have that \[b (q_1 - q_2) = r_2-r_1.\] If $0 \leq r_1 \leq r_2<b$, then $0 \leq b(q_1-q_2)=r_2-r_1<b$. So $q_1-q_2$ is an integer in $[0,1)$ and so must be $0$. Therefore, $q_1=q_2$ and so $r_1=r_2$. Therefore, the quotient and remainder are unique.

It is through a repetition of a variation of this division algorithm that we are able to divide integers with the standard long division algorithm. Look at various ways that we can find the quotient of $284$ by $13$. In particular compare the division algorithm in Theorem 8.1, the standard long division algorithm, the area model, and other models with which you are familiar.

8.1.1 Composing and Decomposing Integers

Numerical fluency involves the ease at which one is able to break apart and recombine numbers under addition and/or multiplication. For addition, the fluency focuses on the tens using items like ten frames. For multiplication, it is a fluency with multiplication facts up to 12s, with flexibility and reversibility.

Related Content Standards

(4.OA.4) Find all factor pairs for a whole number in the range 1-100. Recognize that a whole number is a multiple of each of its factors. Determine whether a given whole number in the range 1-100 is a multiple of a given one-digit number. Determine whether a given whole number in the range 1-100 is prime or composite.

Definition 8.1 Let $a$ and $b$ be integers with $b\neq 0$. We say that $b$ divides $a$, or $b$ is a divisor of $a$, denoted by $b|a$, if there exists a unique $q\in \mathbb{Z}$ such that $a=bq$. So $b$ divides $a$ if and only if $a$ is a multiple of $b$.

We will look at the various properties of the divisors of integers later in this section. But first, we will look at those integers for which there are no divisors other than $1$ and itself.

Definition 8.2 A natural number $p>1$ is prime if the only positive divisors of $p$ are $1$ and $p$. A natural number $n>1$ is composite if it is not prime.

Note that 1 is not a prime number, since prime numbers are defined to be integers greater than 1. The primary reason behind this is to make the prime factorization of the integers unique.

So the prime numbers less than 100 are 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, and 97.

Prime numbers have been studied for centuries, with Euclid proving that there are an infinite number of prime numbers in Proposition 20 of Book IX of the Elements. Over the centuries, many different mathematicians have proven this using various techniques that include the study of Fermat numbers ($F_n=2^{2^n}+1$), group theory, and topology. However, many of the proofs are based on the following lemmas.

Lemma 8.1 If $n$ is a composite, then $n$ is divisible by a prime number.

Proof. Assume that $n$ is a composite number that is not divisible by a prime number. So there are natural numbers $n_1$ and $n_2$, both larger than $1$, such that $n=n_1 \cdot \tilde{n}_1$. From the properties of multiplication of the natural numbers we know that $n_1<n$ and $\tilde{n}_1<n$. Since $n$ is not divisible by a prime number, $n_1$ is a composite number and so we can further factor $n_1$ as a product of natural numbers, $n_2$ and $\tilde{n}_2$. This process will create a sequence of composite numbers, \[n>n_1>n_2>\ldots\] The set of such $n_i$ is a bounded subset of the natural numbers and by the well-ordering property (3.4), there is a least element, $m$. However, this number would be both composite and prime. Since this is not possible, we see that $n$ is divisible by a prime number.

We are now ready to prove the infinitude of the prime numbers.

Theorem 8.2 There are infinitely many prime numbers.

Since we define infinitely many as the negation of finitely many, we will use the technique of “proof by contradition.”

Proof. Assume that there are finitely many prime numbers, \[\left\{ p_1, p_2, p_3, \cdots, p_n\right\}\] with $p_i<p_{i+1}$ for each $1\leq i \leq n$. So we can define a natural number \[m= p_1 \cdot p_2 \cdots p_n +1 = \left( \prod_{i=1}^n p_i \right) +1.\] So for each $1\leq i \leq n$ we have that \[m= p_i \cdot \left(\prod_{j\neq i} p_j\right) +1\] and so by the division algorithm we see that $m$ is not divisible by any of the prime numbers, $p_i$. However, our previous lemma states that this is not possible. Therefore, there are infinitely many prime numbers.

8.1.2 Greatest Common Divisor and Least Common Multiple

Definition 8.3 Let $a$ and $b$ be integers, not both zero. We say that the greatest common divisor (also called the greatest common factor) of $a$ and $b$, denoted $\mathrm{gcd}(a,b)$, is the natural number $d$ such that

$d$ divides both $a$ and $b$, and
if $u$ divides both $a$ and $b$ for some integer $u$, then $u\leq d$.

Let $a$ and $b$ be integers, not both zero. We say that the least common multiple of $a$ and $b$, denoted $\mathrm{lcm}(a,b)$, is the natural number $m$ such that

$m$ is a multiple of both $a$ and $b$, and
if $u$ is a multiple of both $a$ and $b$ for some integer $u$, then $u\geq m$.

Related Content Standards

(6.NS.4) Find the greatest common factor of two whole numbers less than or equal to 100 and the least common multiple of two whole numbers less than or equal to 12. Use the distributive property to express a sum of two whole numbers 1-100 with a common factor as a multiple of a sum of two whole numbers with no common factor.

There are many different options for finding the greatest common divisor and least common multiple of two numbers. If the numbers are small, one can find the greatest common divisor by listing out all of the possible factors of each number and choosing the largest one in common. Another option is using the factor trees of the two numbers, based on the prime factorizations of the numbers.

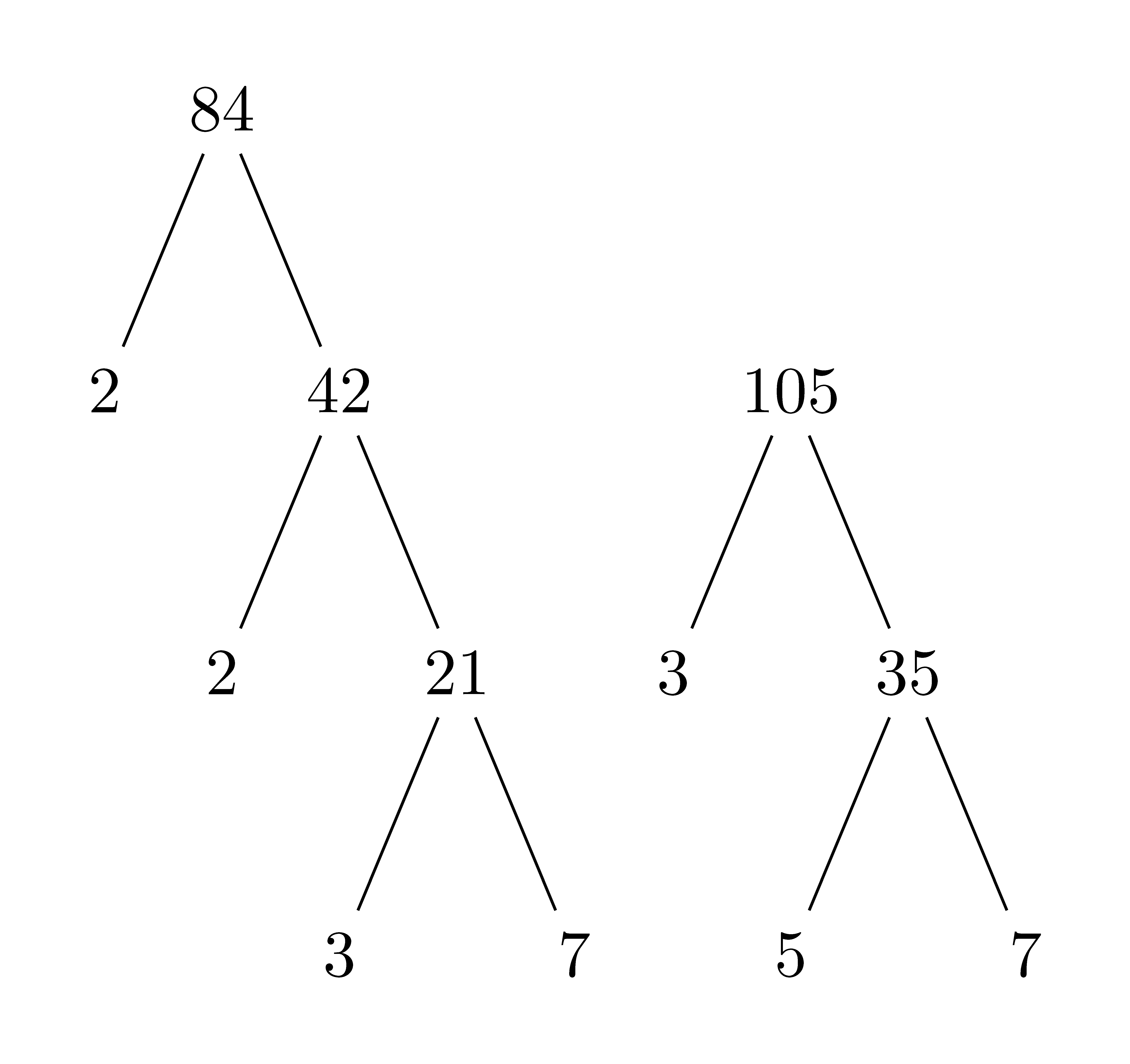
Figure 8.1: Factor Trees

Similarly, for small numbers one can list out the multiples of each number until you find a common multiple, or you can use information from the numbers’ prime factorizations. When the numbers are much larger, one can develop other techniques to create algorithms for finding the greatest common divisor and least common multiple. Many of these techniques are based on the following theorem.

Theorem 8.3 If $a,b,q,r$ are integers, with $a$ and $b$ not both zero, and if \[a=bq+r,\] then $\mathrm{gcd}(a,b)=\mathrm{gcd}(b,r)$.

Proof. Since $a$ and $b$ are not both zero, we let $d=\mathrm{gcd}(a,b)$. This means that there are integers $m$ and $n$ such that $a=md$ and $b=nd$. Therefore, \[r=a-bq=md-(nd)q = d\cdot (m-nq)\] and so $d$ divides $r$ and $d$ divides $b$. Since $d$ is a common divisor of $b$ and $r$, we see that \[\mathrm{gcd}(a,b)\leq \mathrm{gcd}(b,r).\] Since $a=bq+r$, any common divisor of $b$ and $r$ must also be a divisor of $a$, we have that $\mathrm{gcd}(b,r)$ is a common divisor of $a$ and $b$ and so \[\mathrm{gcd}(b,r) \leq \mathrm{gcd}(a,b).\] Therefore, $\mathrm{gcd}(a,b)=\mathrm{gcd}(b,r)$.

Theorem 8.4 (Euclidean Algorithm) Let $a$ and $b$ be two positive integers with $a>b$. Then the greatest common divisor of $a$ and $b$ can be found using the following algorithm.

[Step 1] Apply the division algorithm to find integers $q$ and $r$ such that $a=bq+r$ with $0\leq r<b$.
[Step 2] If $r=0$, then $b$ is $\mathrm{gcd}(a,b)$.
[Step 3] While $r>0$, replace define $a:=b$ and $b:=r$ and apply the division algorithm to the new $a$ and $b$ to generate a new pair of integers $q$ and $r$. Once $r=0$, then the value of $b$ is the greatest common divisor of the original integers $a$ and $b$.

In order to better understand the algorithm, we will find the greatest common divisor of $924$ and $260$. We start by letting $a=924$ and $b=260$. From the division algorithm we find that \[924 = 3 \cdot 260+144.\] We now let $a=260$ and $b=144$ and use the division algorithm again to find that \[260=1\cdot 144 + 116.\] Continuing this process we see that $\mathrm{gcd}(924,260)=4$. \[\begin{align*} 144 &=1\cdot 116 + 28 \\ 116 &= 4 \cdot 28 + 4 \\ 28 &= 7\cdot 4 + 0 \end{align*}\]

8.1.3 Fundamental Theorem of Arithmetic

The most common way to find the greatest common divisor and least common multiple of two numbers is dependent upon the numbers’ prime factorizations. This ability to write a number uniquely as a product of primes is called the Fundamental Theorem of Arithmetic, which we will prove in this section.

We say that two numbers are relatively prime if their greatest common divisor is $1$.

Theorem 8.5 Natural numbers $a$ and $b$ are relatively prime if and only if there exist integers $s$ and $t$ such that $sa+tb=1$.

Proof. Suppose that $a$ and $b$ are relatively prime. From the proof of the Euclidean algorithm we can see that for integers $a$ and $b$ that there exists integers $s$ and $t$ such that $sa+tb=\mathrm{gcd}(a,b)=1$.

Conversely, if there exist integers $s$ and $t$ such that $sa+tb=1$, we know that $d=\mathrm{gcd}(a,b)$ divides $a$ and $b$ and so would also divide $1$. Since the only integers that divide 1 are $1$ and $-1$ and since $\mathrm{gcd}(a,b)\geq 1$, we have that $\mathrm{gcd}(a,b)=1$.

Lemma 8.2 If $p$ is a prime number and $a$ and $b$ are integers such that $p$ divides $ab$, then $p$ divides $a$ or $p$ divides $b$.

Proof. In order to prove the Lemma, we will prove that the negation is false. Suppose that $a$ is relatively prime to $p$ and $b$ is relatively prime to $p$. Then from Theorem 8.5 we have integers $s$, $t$, $u$, and $v$ such that $sa+tp=1$ and $ub+vp=1$. Then \[1= 1 \cdot 1 = (sa+tp)\cdot (ub+vp) = (su)(ab)+(sav+tub+tvp)p\] and so $ab$ and $p$ are relatively prime, implying that $p$ does not divide $ab$.

Theorem 8.6 (Fundamental Theorem of Arithmetic) Every integer $n>1$ can be factored as a product of prime numbers, and except for the order of the factors, this prime factorization is unique.

Proof. Let $n>1$ be an integer. If $n$ is prime, we have a prime factorization of $n$. If $n$ is not prime, then there are integers $n_1$ and $n_2$ such that $n=n_1 n_2$ and we can assume without loss of generality that $1<n_1\leq n_2<n$. If either of these integers are composite, then they also can be factored into factors strictly smaller than them. This process can be continued, but it cannot be continued indefinitely since $n$ is a finite number. At the conclusion of the process, $n$ will have a prime factorization. We now only need to show uniqueness of this factorization.

Assume that $n$ has two distinct prime factorizations, \[n=p_1 p_2 \cdots p_j \quad \mbox{and} \quad n=q_1 q_2 \cdots q_k\] and we can assume without loss of generality that $j\leq k$.

Since $p_1$ divides $n$, a generalization of Lemma 8.2 gives us that $p_1$ must divide one of the $q_i$. By reordering the primes we can label this $q_i$ as $q_1$. Since both $p_1$ and $q_1$ are prime, they must be equal. We can continue this process with $p_2 \cdots p_j$ and $q_2\cdots q_k$ to find that $p_2=q_2$ and continuing the process to equate each of the $p_i$ with a $q_i$. If some of the $q_i$ remain after this process, these would be factors of $1$ and therefore could not be prime. Therefore, $j=k$ and we see that the two prime factorizations are just a reordering of each other.

8.1.4 Exercises

Let $n\in \mathbb{Z}$. What are the possible values for the remainder of $n^2$ with a divisor of $3$? Justify your result.
Find the $q$ and $r$ from the Division Algorithm for the given values of $a$ and $b$.
1. $a=0$, $b=14$
2. $a=-42$, $b=14$
3. $a=9$, $b=14$
Use the Division Algorithm to prove that for positive integers $m$ and $n$, with $m > n$, then exactly one of the following statements must be true:
- There is a positive integer $k$ such that $m = kn$
- There is a positive integer $k$ such that $kn < m < (k + 1)n$
Use the Euclidean Algorithm to find $\mathrm{gcd}(4368,31050)$.
Create a computer program or spreadsheet based on the Euclidean Algorithm that you can use to find the greatest common divisor of two integers.
Prove that for all integers that $\mathrm{gcd}(a,b)\cdot \mathrm{lcm}(a,b) = |ab|$. (Hint: Use the prime factorizations of $a$ and $b$.)