5.1 Definitions of Functions
Currently there are two dominant perspectives for defining a function. The first is the concept of function as a rule or procedure, as is denoted in the Common Core Standard (8.F.1).
Related Content Standards
- (8.F.1) Understand that a function is a rule that assigns to each input exactly one output. The graph of a function is the set of ordered pairs consisting of an input and the corresponding output.
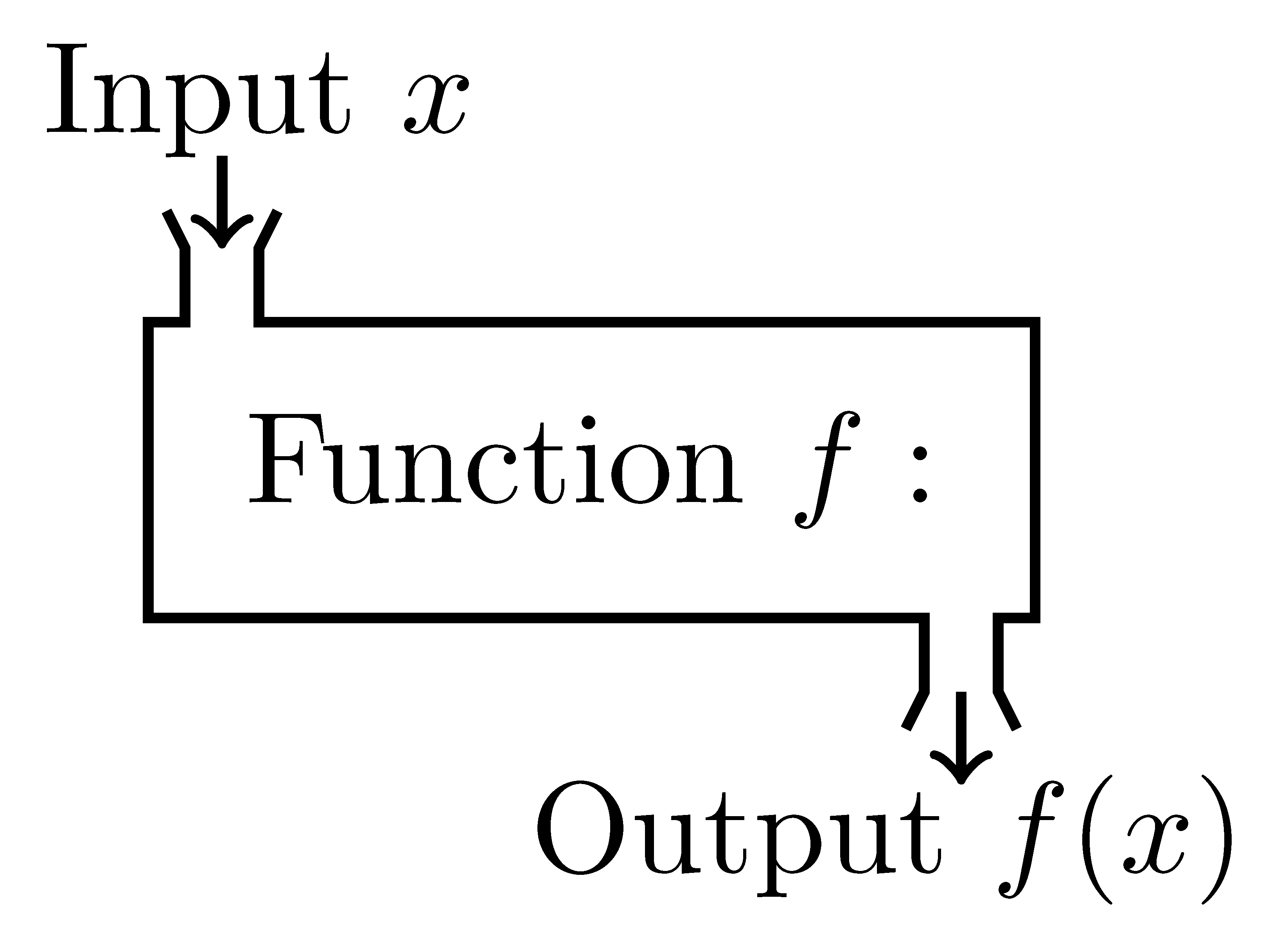
Figure 5.1: Machine analogy of a function
This definition is often represented as a box or machine with certain inputs and outputs as shown in Figure 5.1. This definition of the function, while generally very useful in understanding the use of functions, is not as mathematically sound as the generally accepted definition of function that arose in the early 1900’s and appears in most theoretical mathematics textbooks. One of the main differences between the two definitions is the focus on the function being defined by three items: the domain, the codomain, and the relationship between elements of the two sets.
Definition 5.1 Let \(A\) and \(B\) be two sets, and let \(R\) be a relation from \(A\) to \(B\). Then \(R\) is a function if for every \(a\in A\), there exists a unique \(b\in B\) such that \((a,b)\in R\). The set \(A\) is called the domain of the function and \(B\) is called the codomain of the function.
One should note from this definition of a function that the function is the set of ordered pairs that is often referenced as the graph of the function, rather than the algebraic or tabular representation that the input-output definition implies. Throughout the remainder of the text, we will bounce back and forth between the two views of a function, with the “input-output” or “rule” perspective often being reflected in an algebraic representation of the function and the “relation” or “ordered-pairs” perspective being reflected in a graphical representation of the function.
Related Content Standards
- (HSF.IF.1) Understand that a function from one set (called the domain) to another set (called the range) assigns to each element of the domain exactly one element of the range. If \(f\) is a function and \(x\) is an element of its domain, then \(f(x)\) denotes the output of \(f\) corresponding to the input \(x\). The graph of \(f\) is the graph of the equation \(y = f(x)\).
In both of these definitions we talk about the function as a relation between two sets, the domain \(A\) and the codomain \(B\), and we often denote the function as \(f:A \rightarrow B\). The subset of the co-domain \[\mbox{Ran}(f)=\left\{b\in B \: \middle \vert \: b=f(a) \mbox{ for some } a \in A\right\}\] is called the range of the function. This is different than the usual definitions in the K-12 mathematics textbooks and in the Common Core State Standards where authors do not define the co-domain because it is almost always assumed to be the real numbers.
Figure 5.2: Concept sketch of \(f:A \rightarrow B\)
So the codomain is the set with all of the possible outputs of the function, while the range is the actual outputs of the function. So we can see that \(\mathrm{Range}(f) \subseteq \mathrm{Codomain}(f)\).
One of the key distinctions between relations that represent functions and those that do not has to do with the uniqueness of the element in the co-domain that is related to each element in the domain. For instance, with the relation from \(x\) to \(y\) given by \(y=5x\), each value of \(x\) has only one value of \(y\) related to it. However, with the relation on \([-1,1]\times [-1,1]\) given by \(x^2+y^2=1\), each value of \(x\) has two distinct values of \(y\) related to it and so \(y\) is not a function of \(x\).
If one has the graphical representation of a relation available, one can determine if the relation represents a function by seeing if there is any value in the domain that has multiple values in the co-domain by looking for a vertical line that intersects the graph of the function at multiple points (Vertical Line Test). Thus the relation on \(\mathbb{R}\times \mathbb{R}\) given by \(y^2=x\) does not represent \(y\) as a function of \(x\), but it does represent \(x\) as a function of \(y\).
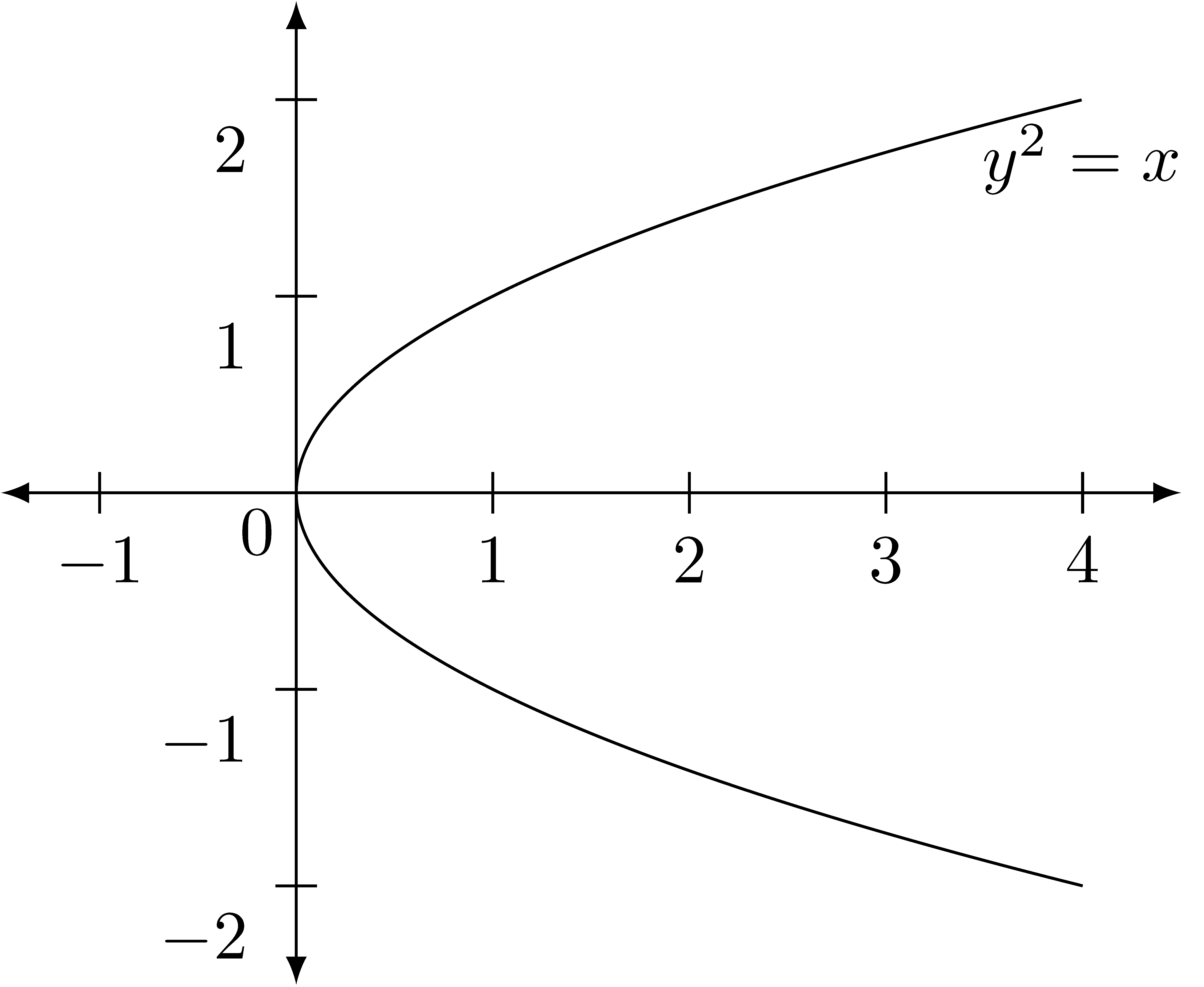
5.1.1 Function Representations
In order to understand the different representations for a function we will use the squaring function, \(f:\mathbb{R}\rightarrow \mathbb{R}\), that is often represented by \(f(x)=x^2\), or equivalently \(x\mapsto x^2\).
If we use the sets and relation definition of the function, this function is defined to be \[f= \left\{ (x,y)\in \mathbb{R}^2 \middle \vert y=x^2\right\}.\] This is often represented graphically as
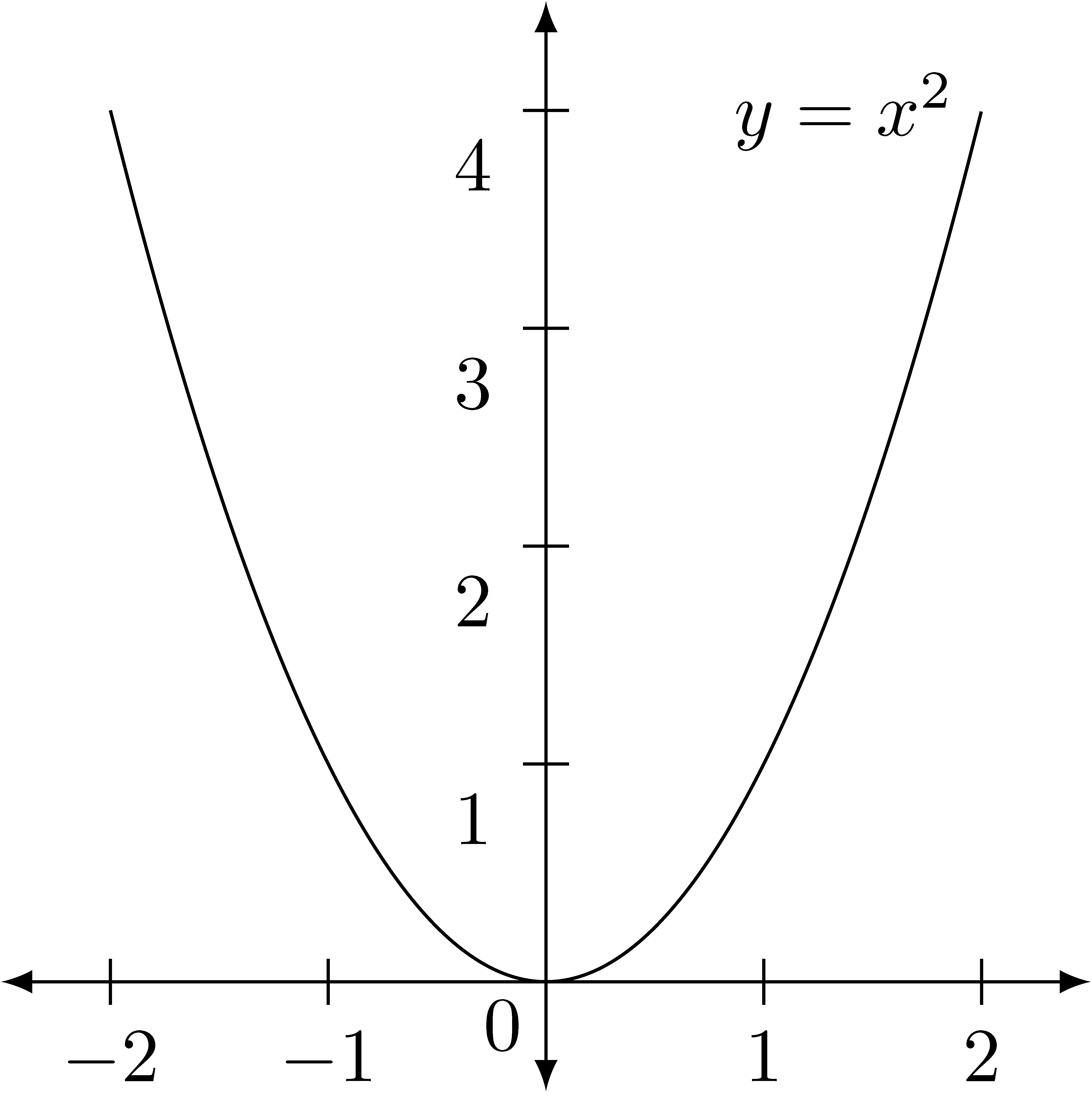
If we restrict the domain and co-domain to be natural numbers, so that \(f:\mathbb{N}\rightarrow \mathbb{N}\), we can represent the function in a tabular format
| \(x\) | \(y\) |
|---|---|
| 0 | 0 |
| 1 | 1 |
| 2 | 4 |
| 3 | 9 |
| \(\vdots\) | \(\vdots\) |
or by mapping elements from the domain to the co-domain
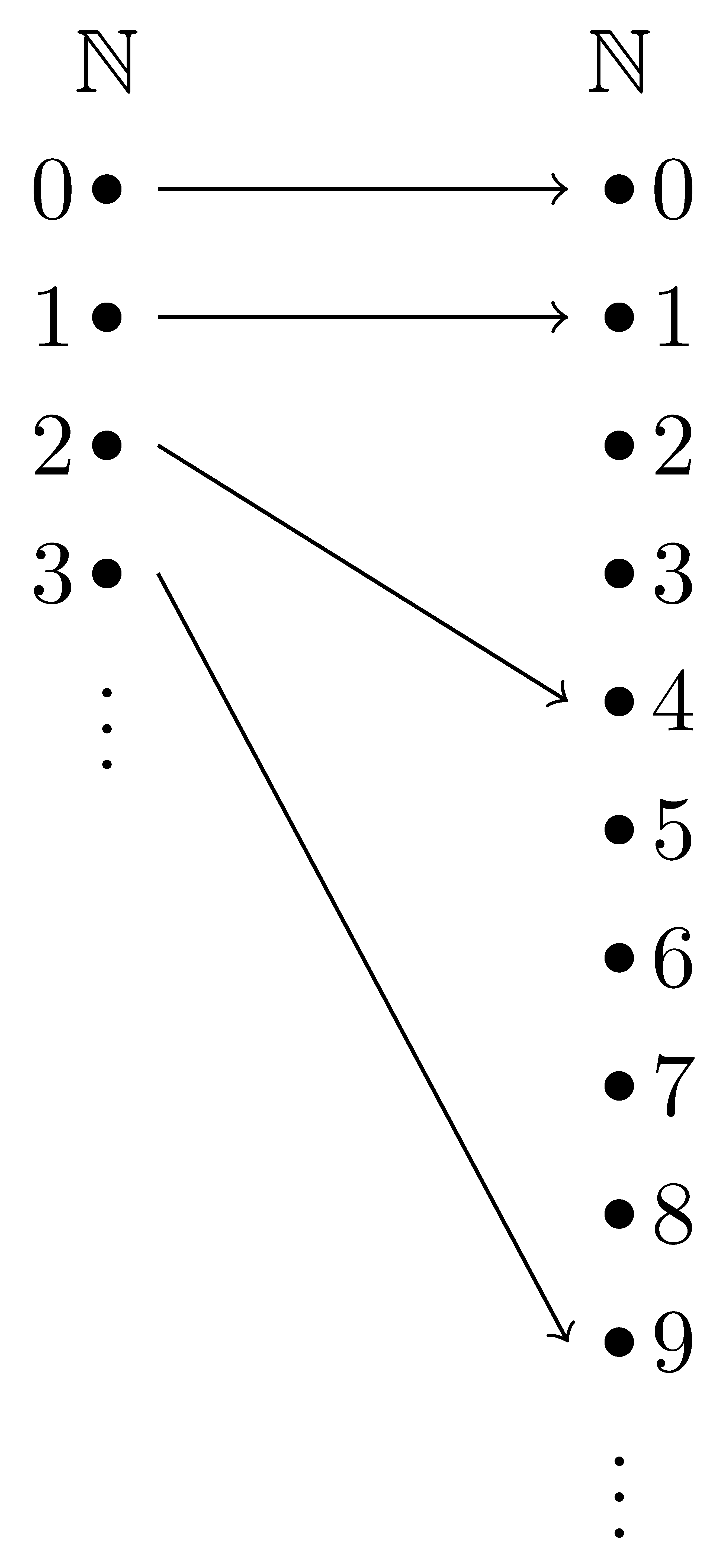
So the range of this squaring function is the square numbers, \(\{0,1,4,9,16, \ldots\}\subset \mathbb{N}\).
There are some times where it is easier to start describing the function by sketching how elements from the domain map to the co-domain. For example, if the function, \(f:\mathbb{N}\rightarrow \mathbb{Z}\), is defined by the relationship
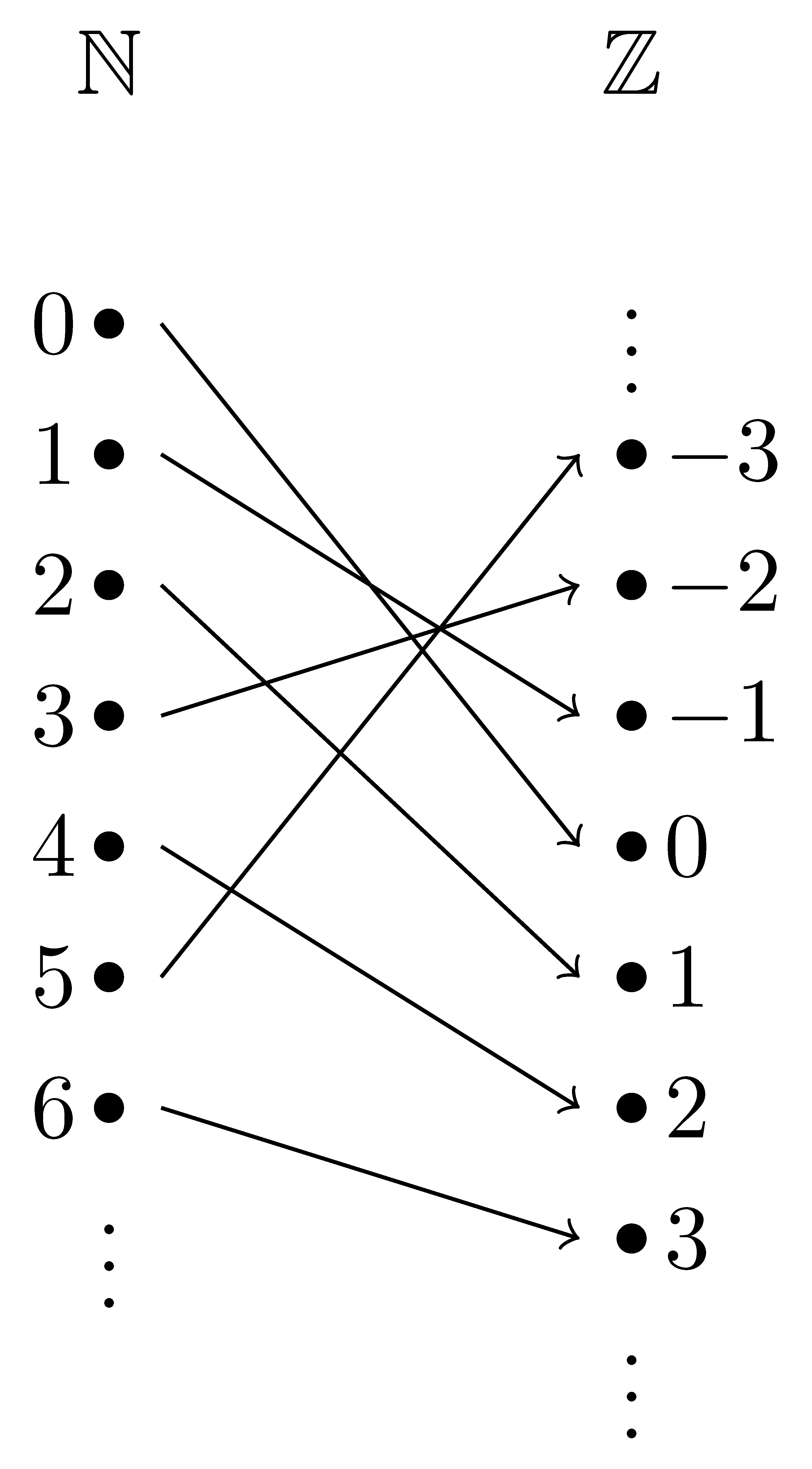
where each successive even natural number maps to the next larger positive integer and each successive odd natural number maps to the next negative integer. This function can also be represented by the graph
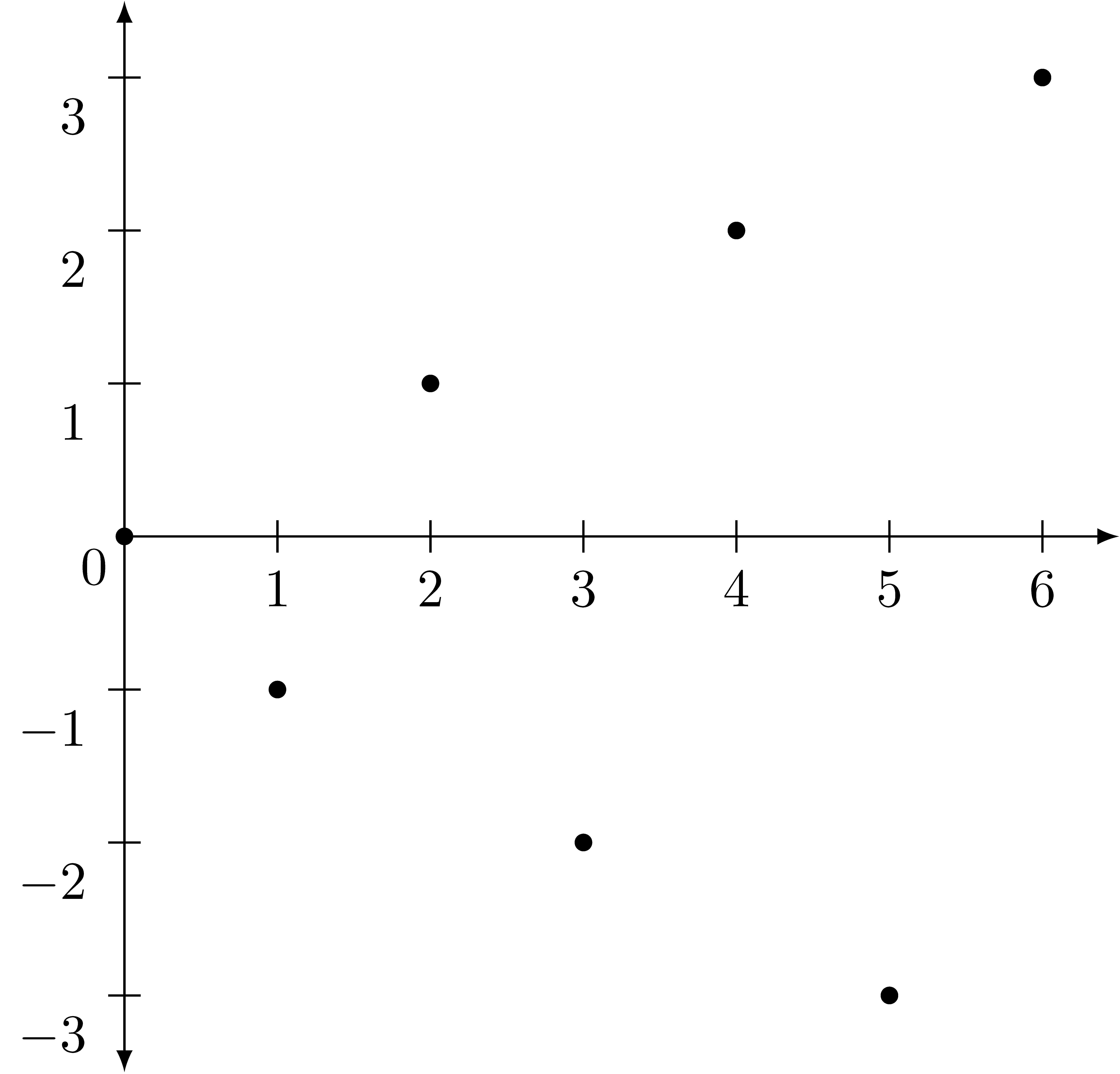
and it can be represented algebraically as \[f(n) = \begin{cases} -\frac{n+1}{2} & \mbox{if } n \mbox{ is odd}\\ \frac{n}{2} & \mbox{if } n \mbox{ is even} \end{cases} \quad \mbox{or} \quad f(n)=(-1)^n\frac{2n+1-(-1)^n}{4}.\]
5.1.2 Exercises
Let \(A=\{a,b,c\}\) and let \(B=\{1,2\}\). List all of the possible functions from \(A\) to \(B\).
Define \(\mathrm{sum}:\mathbb{N}\times \mathbb{N} \rightarrow \mathbb{N}\) by \((m,n) \mapsto m+n\). Show that \(\mathrm{sum}\) is a function.
Describe how the content of this section relates to the statement, “You can’t take the square root of a negative number.”
Which of the following are functions? For those that are not functions, explain why not. For those that are functions, list the domain, range, and codomain of the function.
\(f:\mathbb{R} \rightarrow \mathbb{R}\), with \(f(x)=\frac{1}{x}\).
\(f= \{(x,y)\in \mathbb{R}^2\vert \: x^2+y^2=1\}\)
\(f= \{(x,y) \in [-1,1]\times [0,1] \vert \: x^2+y^2=1\}\)
\(g:[0,\infty) \rightarrow \mathbb{R}\), with \(g(x)=\sqrt{x}\).
\(h:\mathbb{N} \rightarrow \mathbb{N}\), with \(h(x)=x^2\).
Let \(f:A\rightarrow B\) be a function. Define a relation on \(A\) by \[a_1 \sim_f a_2 \Leftrightarrow f(a_1)=f(a_2)\] for all \(a_1,a_2\in A\).
Show that \(\sim_f\) is an equivalence relation.
If \(f:\mathbb{R} \rightarrow \mathbb{R}\) is defined by \(f(x)=\sin(2\pi x)\), find the equivalence class of \(0\) under this equivalence relation.