11.3 Measurements of Triangles

A key aspect of measurement in geometry involves the relationships between the lengths of sides of a triangle.

Related Content Standards

(8.G.6) Explain a proof of the Pythagorean Theorem and its converse.
(8.G.7) Apply the Pythagorean Theorem to determine unknown side lengths in right triangles in real-world and mathematical problems in two and three dimensions.
(8.G.8) Apply the Pythagorean Theorem to find the distance between two points in a coordinate system.

Theorem 11.2 (Pythagorean Theorem) For a right triangle with side lengths \(a\) and \(b\), and hypotenuse \(c\), \[a^2+b^2=c^2.\]

Proof. For any right triangle with side lengths \(a\) and \(b\), and hypotenuse \(c\), we construct a square of side lengths \(a+b\). We can then construct a figure of four copies of the original right triangle, so that each side length is composed of one copy of each leg of the triangle.

Since we have right triangles on each corner of the square, we can use the properties of congruent triangles to show that the four triangles are congruent, meaning that the interior quadrilateral is a rhombus.

Since the four triangles are congruent, the two angles at each point of intersection between the two quadrilaterals must add to a right angle. So the interior quadrilateral is also a square.

So the area of the larger square can be written in two different ways, as a single square and as the sum of the smaller square and the four triangles, \[(a+b)^2 = c^2 + 4 \cdot \left( \frac{1}{2} ab \right) .\] Rearranging the terms we have that \[a^2+2ab+b^2 = c^2+2ab\] and so we have that \[a^2+b^2=c^2.\]

Proposition 11.1 (Euclid's Proposition 20: Triangle Inequality) In any triangle two sides taken together in any manner are greater than the remaining one.

Proof. Let \(\triangle ABC\) be a triangle.

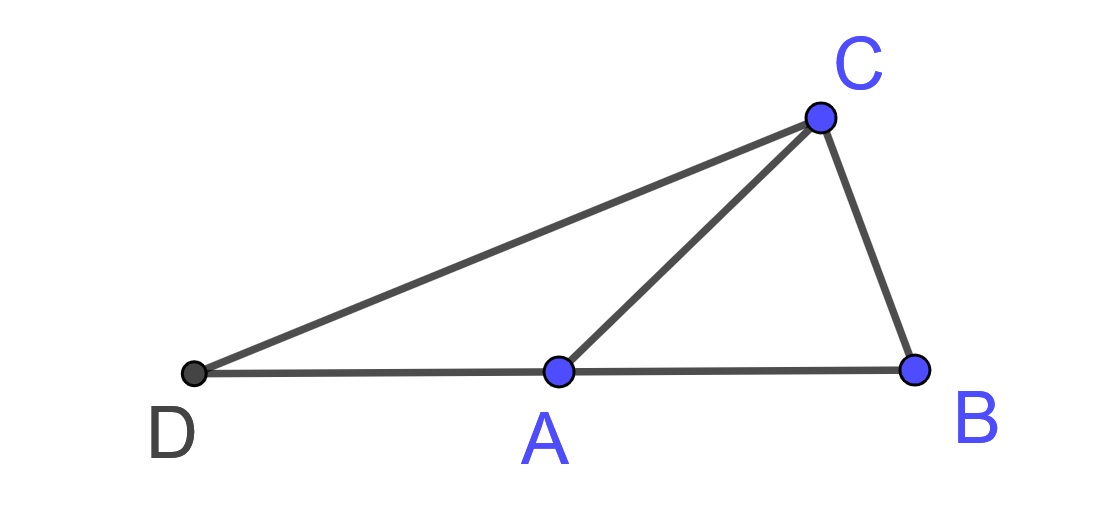
Extend \(BA\) through to the point \(D\) so that \(DA\) is equal to \(CA\). Create the finite segment \(DC\) to create the triangle \(\triangle ACD\). Since \(AD\) equals \(AC\), \(\triangle ACD\) is isosceles and so the angles \(\angle ACD\) and \(\angle ADC\) are equal. So \(\angle BCD\) is greater than \(\angle ADC\).

Since \(\triangle DCB\) is a triangle having the angle \(\angle BCD\) greater than the angle \(\angle BDC\), and the side opposite the greater angle is greater, therefore \(DB\) is greater than \(BC\).

But \(DA\) equals \(AC\), therefore the sum of \(BA\) and \(AC\) is greater than \(BC\).

Similarly we can prove that the sum of \(AB\) and \(BC\) is also greater than \(CA\), and the sum of \(BC\) and \(CA\) is greater than \(AB\).

Therefore, in any triangle, the sum of any two sides is greater than the remaining one.

Proposition 11.2 (Euclid's Proposition 22) Out of three straight lines, which are equal to three given straight lines, to construct a triangle: thus it is necessary that two of the straight lines taken together in any manner should be greater than the remaining one.

Proof. Let the three given straight lines be \(a\), \(b\), and \(c\), and let the sum of any two of these be greater than the remaining one, namely, \(a\) plus \(b\) greater than \(c\), \(a\) plus \(c\) greater than \(b\), and \(b\) plus \(c\) greater than \(a\).

Set out a straight line DE, terminated at D but of infinite length in the direction of E. Make DF equal to \(a\), FG equal to \(b\), and GH equal to \(c\).

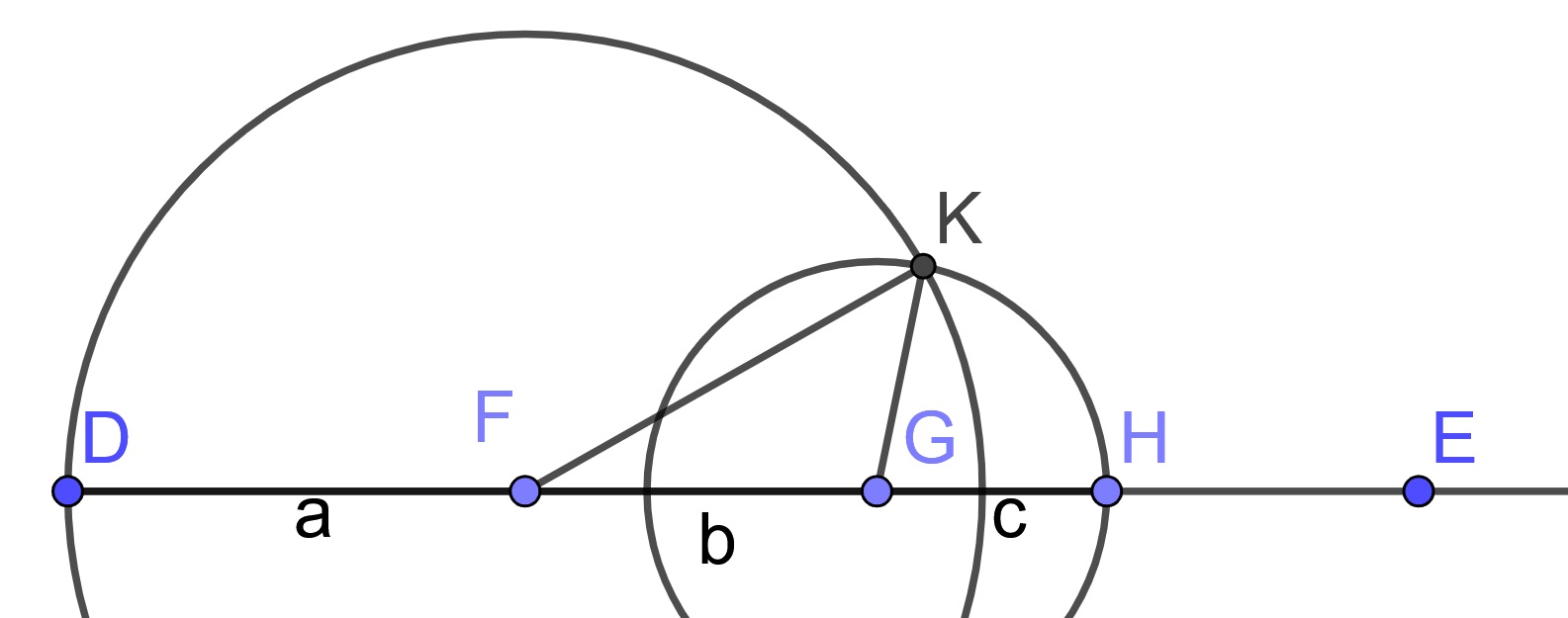
Construct the circle centered at \(F\) through the point \(D\) and the circle centered at \(G\) through the point \(H\). The two circles intersect due to the relationships between \(a\), \(b\), and \(c\). Let \(K\) be one of the points of intersection.

Then the triangle \(\triangle FKG\) has the desired side lengths.

Theorem 11.3 (Converse of Pythagorean Theorem) For any three positive numbers \(a\), \(b\), and \(c\) such that \(a^2 + b^2 = c^2\), there exists a triangle with sides \(a\), \(b\) and \(c\), and every such triangle has a right angle between the sides of lengths \(a\) and \(b\).

Proof. Let \(a\), \(b\), and \(c\) be three positive numbers such that \(a^2+b^2=c^2\).

Since \[(a+b)^2 = a^2+2ab+b^2 = c^2 + 2ab,\] \(c<a+b\).

Since \[(a-b)^2 = a^2-2ab+b^2 = c^2-2ab,\] \(a-b<c\).

By Proposition 11.2, we know that a triangle with sides \(a\), \(b\), and \(c\) exists. We will label the triangle \(\triangle ABC\) with \(AB\) having length \(c\), \(AC\) having length \(b\), and \(BC\) having length \(a\).

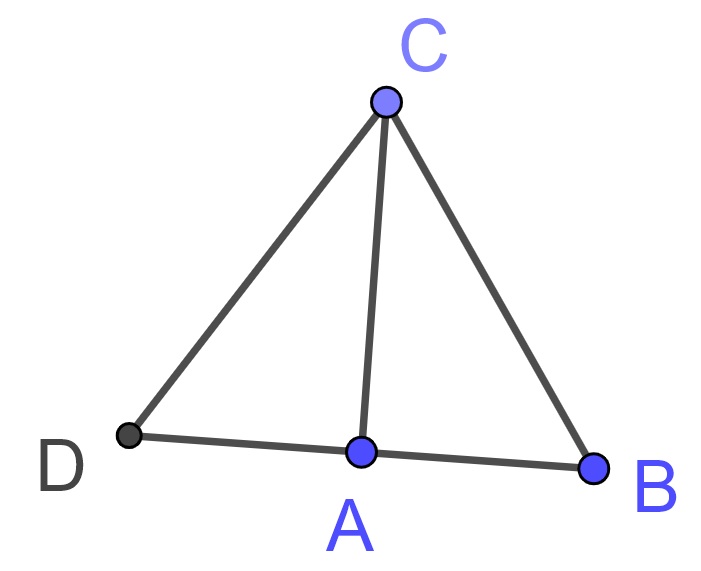
Let \(D\) be a point such that \(AD\) is perpendicular to \(AC\) and \(AD\) equals \(AB\). Since triangle \(\triangle ACD\) is a right triangle, the Pythagorean theorem implies that \(CD\) must have side length \(a\) and so is equal to \(BC\). Hence the side lengths of \(\triangle ADC\) all equal the side lengths of \(\triangle ABC\). So \(\triangle ADC\) is congruent to \(\triangle ABC\) by Proposition 10.8 (SSS). Since the angle \(\angle DAC\) is a right angle, so is \(\angle BAC\).

11.3.1 Exercises

Consider an equilateral triangle with a 1 unit side length. Sketch such a triangle and draw an altitude. Find the exact height of the altitude.
Consider a right isosceles triangle with legs 1 unit long. Find the exact length of the hypotenuse.
A square is inscribed with a circle such that the four corners of the square sit on the circumference of the circle. The square has side length 1 unit in length. Find the exact diameter of the circle.
A rectangle is inscribed within a circle such that the four corners of the rectangle lie on the circle’s circumference. The radius of the circles is 1 unit long. If the base of the rectangle is 1.2 units long, find the height of the rectangle.
An equilateral triangle is inscribed in a circle of radius r. Using only algebra and Pythagorean relationships (e.g., no trigonometric functions), find an expression for the length of the side length of the triangle in terms of r.