10.1 Definitions
Cultures define words through agreement over time and throughout the culture about the meanings of the words. In most languages, words correspond to multiple definitions or ideas that often depend upon the context and situation to derive the meaning implied. The creation of new definitions and new words often arises from the usage of the words in new ways. For example, the definition of the word ‘Google’ includes the search for something on the internet, perhaps without even using the search engine created by the company with that name (Edwards & Ward, 2008).
In the language of mathematics, such language is too vague for logical reasoning and determining the truth value of a statement. Mathematical definitions are much more precise and have only one meaning that is usually stipulated at the beginning of the mathematical argument in order to make sure that the one communicating and the one receiving the communication have a well-agreed upon definition. This precision of language is one of the core components of the sixth Standard for Mathematical Practice.
Related Content Standards
- (SMP.6) Attend to precision.
Mathematically proficient students try to communicate precisely to others. They try to use clear definitions in discussion with others and in their own reasoning. They state the meaning of the symbols they choose, including using the equal sign consistently and appropriately. They are careful about specifying units of measure, and labeling axes to clarify the correspondence with quantities in a problem. They calculate accurately and efficiently, express numerical answers with a degree of precision appropriate for the problem context. In the elementary grades, students give carefully formulated explanations to each other. By the time they reach high school they have learned to examine claims and make explicit use of definitions.
Though mathematical definitions are precise, they are not always agreed upon among the general mathematical community. Consider the following two definitions of a circle.
- A circle is a plane figure contained by one [curved] line such that all the straight lines falling upon it from one point among those lying within the figure are equal to one another.
- A circle is the set of points in the plane that are equidistant from a single fixed point.
Both definitions of a circle are equally valid, but they refer to two very different objects. The second definition defines the circle as the curve, in which case the circle has no area. The first definition defines the circle as the part of the plane contained within the curve. This illustrates the importance of defining the terms well at the beginning of the argument to make sure that all parties agree upon the definition referenced in the argument.
Related Content Standards
- (HSG.CO.1) Know precise definitions of angle, circle, perpendicular line, parallel line, and line segment, based on the undefined notions of point, line, distance along a line, and distance around a circular arc.
10.1.1 Criteria for Definitions
In the creation of mathematical definitions, Van Dormolen & Zaslavsky (2003) list four criteria as essential and three criteria as preferential.
Hierarchy - When defining new mathematical objects, one should take care to not use mathematical objects that have not been previously defined. For example, one cannot define a right angle without first defining an angle.
Existence - While one can define a mathematical object using previously defined objects, unless we can also show the existence of such an object, the mathematical logic and proofs regarding that object are irrelevant. For example, we proved the existence of our various number systems by construction in Chapter 4 and we will begin our study of geometry by proving that many geometric objects exist by constructing such objects using a straightedge and compass.
Equivalence - Some mathematical objects can have multiple definitions equivalent to one another. For instance, one could define an equilateral triangle as a triangle with three equal sides or as a triangle with three equal angles. However, in order to build a consistent system, one of these must be chosen as the definition and the other as a theorem. Then the theorem must be proven to be equivalent to the definition. Then either could be used to prove further properties of equilateral triangles.
Axiomatization - The final necessary property of a mathematical definition is that it must be part of a larger axiomatic system. Definitions involving number systems are usually a part of an axiomatic system built upon set theory. Definitions in geometry are usually within an axiomatic geometric system similar to that of Euclid. In order to have a hierarchy of definitions, there must be a set of foundational definitions. Such foundational definitions are the axioms of the system.
While lacking any of the above criteria could result in logical contradictions or fallacies, the next three criteria are a part of the beauty and elegance of mathematics.
Minimality - One could define a square as being a quadrilateral with four equal sides, four right angles, two pairs of parallel sides, and whose diagonals bisect one another at right angles. However, many components of the definition are a direct result of other components. Thus, a desirable property in mathematics is to reduce the definition to the minimal amount of requirements in order to better understand the mathematical structures related to the mathematical objects. So a square can be defined as an equilateral and equiangular quadrilateral.
Elegance - When two equivalent definitions exist for a mathematical object, one must make the decision as to which to make the definition and which to make a theorem. Generally, the one chosen as the definition for the object is the one that looks nicer, has fewer words or symbols, and uses more basic mathematical concepts. Such a decision is often subjective as elegance is often in the eye of the beholder.
Degenerations - A degenerate case in a class of objects is one that appears to be qualitatively different from the rest of the class. When a mathematical definition is created, we want to eliminate as many of the degenerate cases as possible. Van Dormolen & Zaslavsky (2003) describe this very well with the following example.
Definition 10.1 A quadrilateral is a set of four points \(A, B, C, D\) of which no three are collinear and four segments \(AB, BC, CD, DA\).
Each of the examples in Figure 10.1 satisfies the condition of the definition.
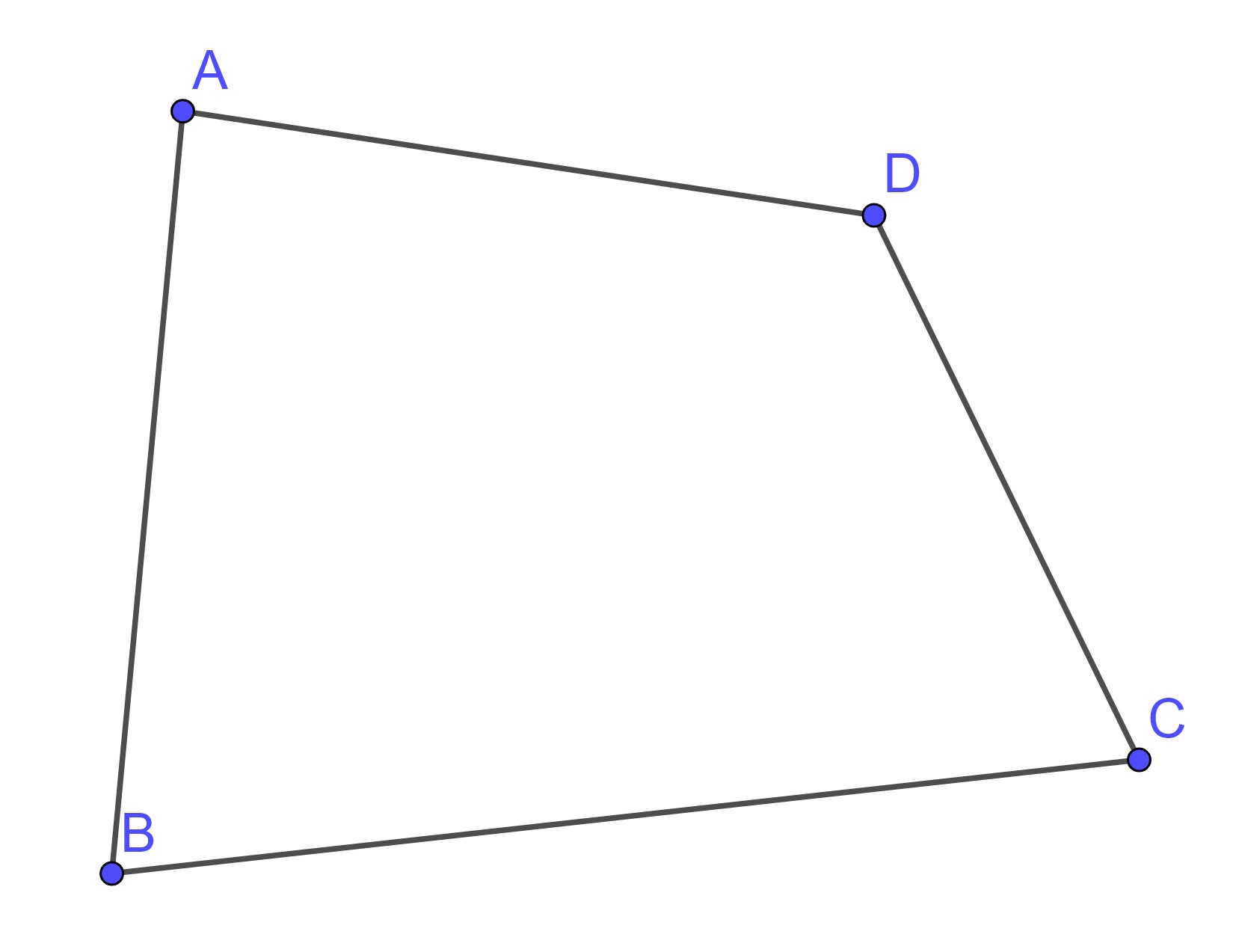
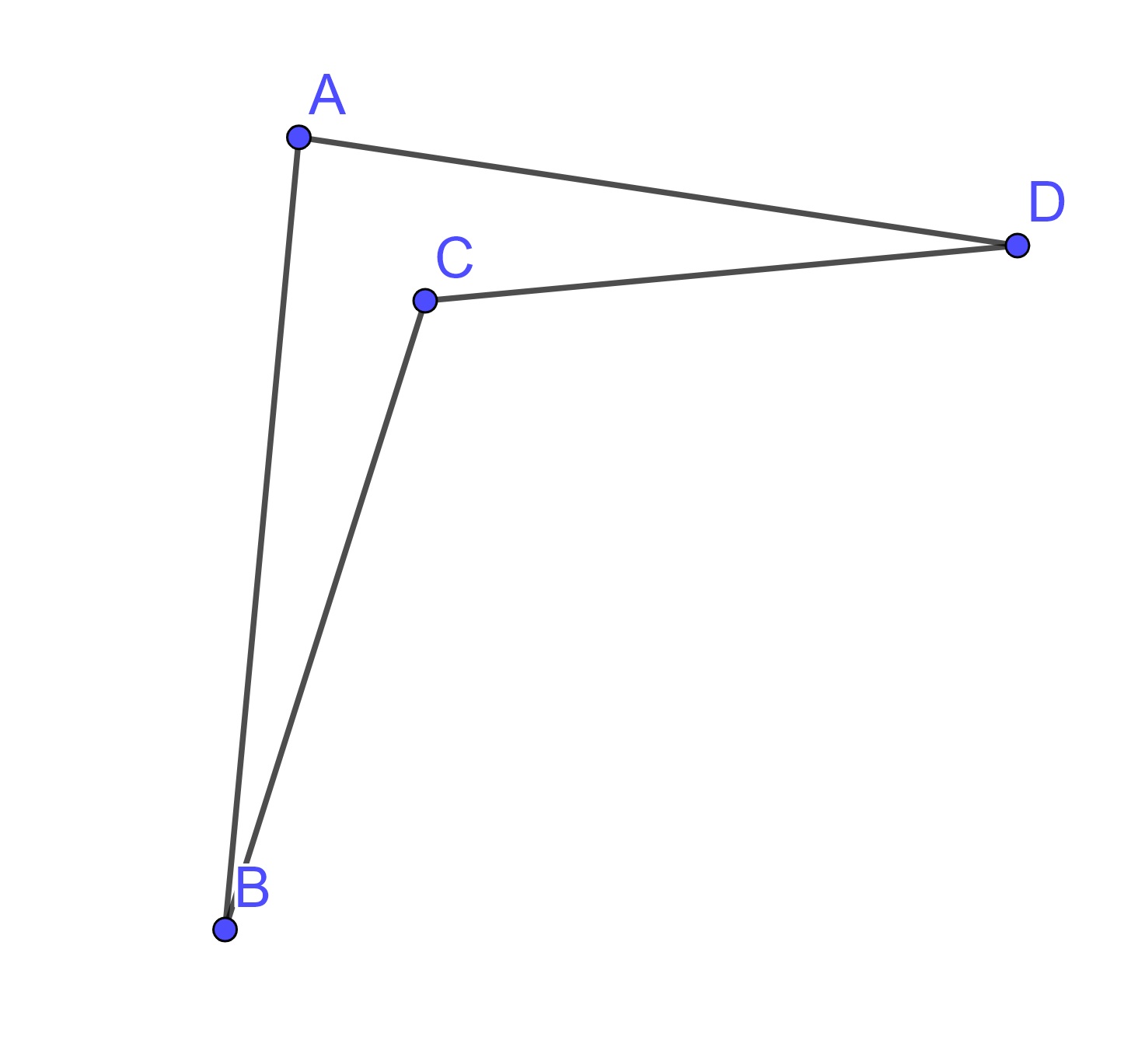
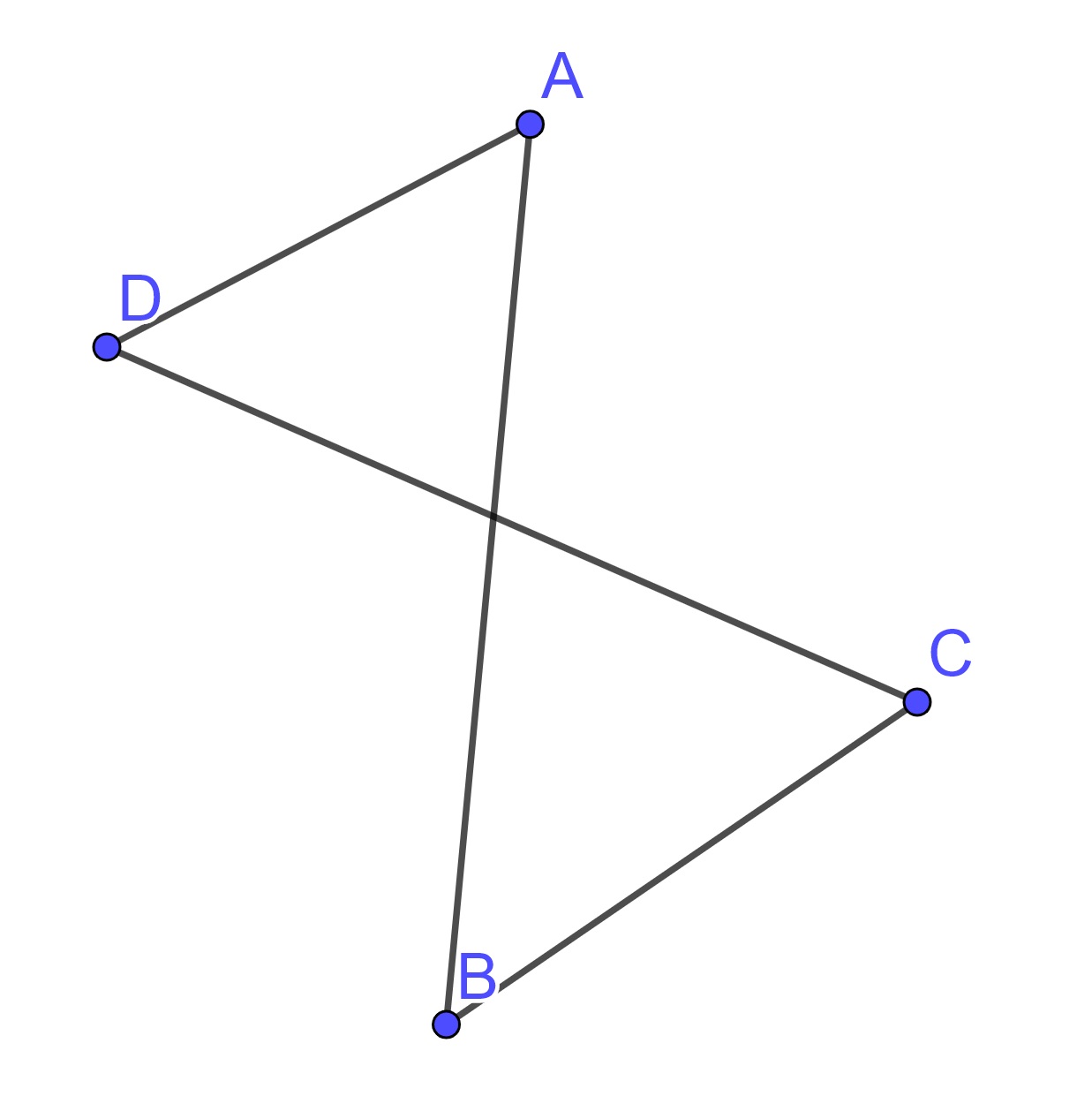
Figure 10.1: Examples of Quadrilaterals
However, one has the intuition that the third case should not be included and is a degeneration of what is intuitively considered a quadrilateral. Because of this, such a definition of quadrilaterals would be rejected and replaced with a definition that does not include such degenerations. The most common method of removing these types of quadrilaterals is to require the sides of the quadrilateral to not be self-intersecting.
10.1.2 Concept Image
While the mathematical definition of an object or concept is essential to precise communication and the axiomatization of mathematical structures and systems, less formal understandings of the mathematical concept are essential. Visual representations, mental pictures, and experiences associated with a mathematical concept combine to create a concept image. When one thinks about a square, one often does not first think about the precise mathematical definition of a square, but instead has many examples of squares (usually visual) in their mind, along with various properties of squares learned through prior experiences (Vinner, 1991). Such concept images “may be incomplete or mathematically incorrect, and can include naïve, non-mathematical associations with the concept name” (Edwards & Ward, 2008, p. 224).
![Interplay between definition and image [@Vinner1991,p. 71]](images/concept-image.jpg)
Figure 10.2: Interplay between definition and image (Vinner, 1991, p. 71)
When presenting mathematical tasks to students, our ideal is that the students draw upon a mixture of concept definitions and concept images in order to interact with the task as seen in Figure 10.2. However, most often students default is to only address the task through their concept images.
10.1.3 Classification of Two-Dimensional Figures
A good example in the K-12 curriculum where the precision of definitions arise is in the classification of two-dimensional planar figures.
Related Content Standards
- (3.G.1) Understand that shapes in different categories (e.g., rhombuses, rectangles, and others) may share attributes (e.g., having four sides), and that the shared attributes can define a larger category (e.g., quadrilaterals). Recognize rhombuses, rectangles, and squares as examples of quadrilaterals, and draw examples of quadrilaterals that do not belong to any of these subcategories.
- (4.G.2) Classify two-dimensional figures based on the presence or absence of parallel or perpendicular lines, or the presence or absence of angles of a specified size. Recognize right triangles as a category, and identify right triangles.
- (5.G.3) Understand that attributes belonging to a category of two-dimensional figures also belong to all subcategories of that category. For example, all rectangles have four right angles and squares are rectangles, so all squares have four right angles.
- (5.G.4) Classify two-dimensional figures in a hierarchy based on properties.
As we see below, the definitions of the two-dimensional figures referenced in these standards are not standardized.
10.1.3.1 Rhombus Definitions
- Euclid: Of quadrilateral figures, \(\ldots\) a rhombus that which is equilateral but not right-angled.
- Illustrative Mathematics: Rhombus: A parallelogram with 4 sides with equal length. (A parallelogram is defined to be a quadrilateral with 2 pairs of parallel sides.)
- Eureka Math/EngageNY: A rhombus is a quadrilateral with all sides of equal length.
We can see from these definitions that the Euclidean definition excludes squares from being rhombi, while the other two definitions include squares. We can also see that the Illustrative Mathematics definition is not as minimal as the Eureka Math/EngageNY definition. There may be strong pedagogical reasons for avoiding minimality, but it is important for the teacher to know which properties can be derived from other properties.
For further study in this area, Usiskin & Griffin (2008) give a detailed description of the role of definition in the classification of quadrilaterals.
10.1.4 Definitions from Euclid’s Elements
Consider the following definitions from Euclid’s Elements (Heath, 1908a, pp. 153–154), paying particular attention to the various criteria of definitions listed in this section. As new concepts are defined, compare those definitions to your current concept images.
- A point is that which has no part.
- A line is a breadthless length.
- The extremities of a line are points.
- A straight line is a line which lies evenly with the points on itself.
- A surface is that which has length and breadth only.
- The extremities of a surface are lines.
- A plane surface is a surface which lies evenly with the straight lines on itself.
- A plane angle is the inclination to one another of two lines in a plane which meet one another and do not lie in a straight line.
- And when the lines containing the angle are straight, the angle is called rectilineal.
- When a straight line set up on a straight line makes the adjacent angles equal to one another, each of the equal angles is right, and the straight line standing on the other is called a perpendicular to that on which it stands.
- An obtuse angle is an angle greater than a right angle.
- An acute angle is an angle less than a right angle.
- A boundary is that which is an extremity of anything.
- A figure is that which is contained by any boundary or boundaries.
- A circle is a plane figure contained by one line such that all the straight lines falling upon it from one point among those lying within the figure are equal to one another;
- And the point is called the centre of the circle.
- A diameter of the circle is any straight line drawn through the centre and terminated in both directions by the circumference of the circle, and such a straight line also bisects the circle.
- A semicircle is the figure contained by the diameter and the circumference cut off by it. And the centre of the semicircle is the same as that of the circle.
- Rectilineal figures are those which are contained by straight lines, trilateral figures being those contained by three, quadrilateral those contained by four, and multilateral those contained by more than four straight lines.
- Of trilateral figures, an equilateral triangle is that which has its three sides equal, an isosceles triangle that which has two of it sides alone equal, and a scalene triangle that which has its three sides unequal.
- Further, of trilateral figures, a right-angled triangle is that which has a right angle, and obtuse-angled triangle that which has an obtuse angle, and an acute-angled triangle that which has its three angles acute.
- Of quadrilateral figures, a square is that which is both equilateral and right-angled; an oblong that which is right-angled but not equilateral; a rhombus that which is equilateral but not right-angled; and a rhomboid that which has its opposite sides and angles equal to one another but is neither equilateral nor right-angled. And let quadrilaterals other than these be called trapezia.
- Parallel straight lines are straight lines which, being in the same plane and being produced indefinitely in both directions, do not meet one another in either direction.
10.1.5 Exercises
Classify the quadrilateral figures defined in the definitions from Euclid’s Elements (square, oblong, rhombus, rhomboid, trapezia) in a hierarchy and draw several examples of each type of quadrilateral.
Consider the following definitions.
Given two fixed points \(F_1, F_2\) called the foci and a distance \(2a\) which is greater than the distance between the foci, the ellipse is the set of points \(P\) such that the sum of the distances \(|PF_{1}|, |PF_{2}|\) is equal to \(2a\).
Given a fixed point \(F_3\) called the center and a distance \(r>0\), the circle is the set of points \(P\) such that the distance \(|PF_3|\) is equal to \(r\).
According to these definitions, is a circle an ellipse? (Explain your reasoning)
Consider the criteria for definitions in this section. What are some of the benefits and drawbacks of these criteria in relationship to K-12 teaching?