9.5 Quadratic Polynomials
Related Content Standards
- (HSF.IF.8) Write a function defined by an expression in different but equivalent forms to reveal and explain different properties of the function.
- Use the process of factoring and completing the square in a quadratic function to show zeros, extreme values, and symmetry of the graph, and interpret these in terms of a context.
Quadratic functions are polynomials whose highest non-zero coefficient is of degree \(2\) and are often written in the form \[f(x)=a_0 + a_1 x + a_2 x^2.\] In order to avoid the use of indices for students when they are working with these quadratic functions, we write them in the form \[f(x)=ax^2 + bx +c.\]
9.5.1 Completing the Square
To better understand the graph of these quadratics, we will modify this form of the quadratic function using a process called completing the square. In this process we rewrite the polynomial in order to find a monic polynomial without a constant coefficient, \[f(x) = a \left( x^2 +\frac{b}{a}x \right) + c.\]
We now look at the area model for the polynomial \(x^2+\frac{b}{a}x\) by splitting the \(\frac{b}{a}x\) into two pieces.
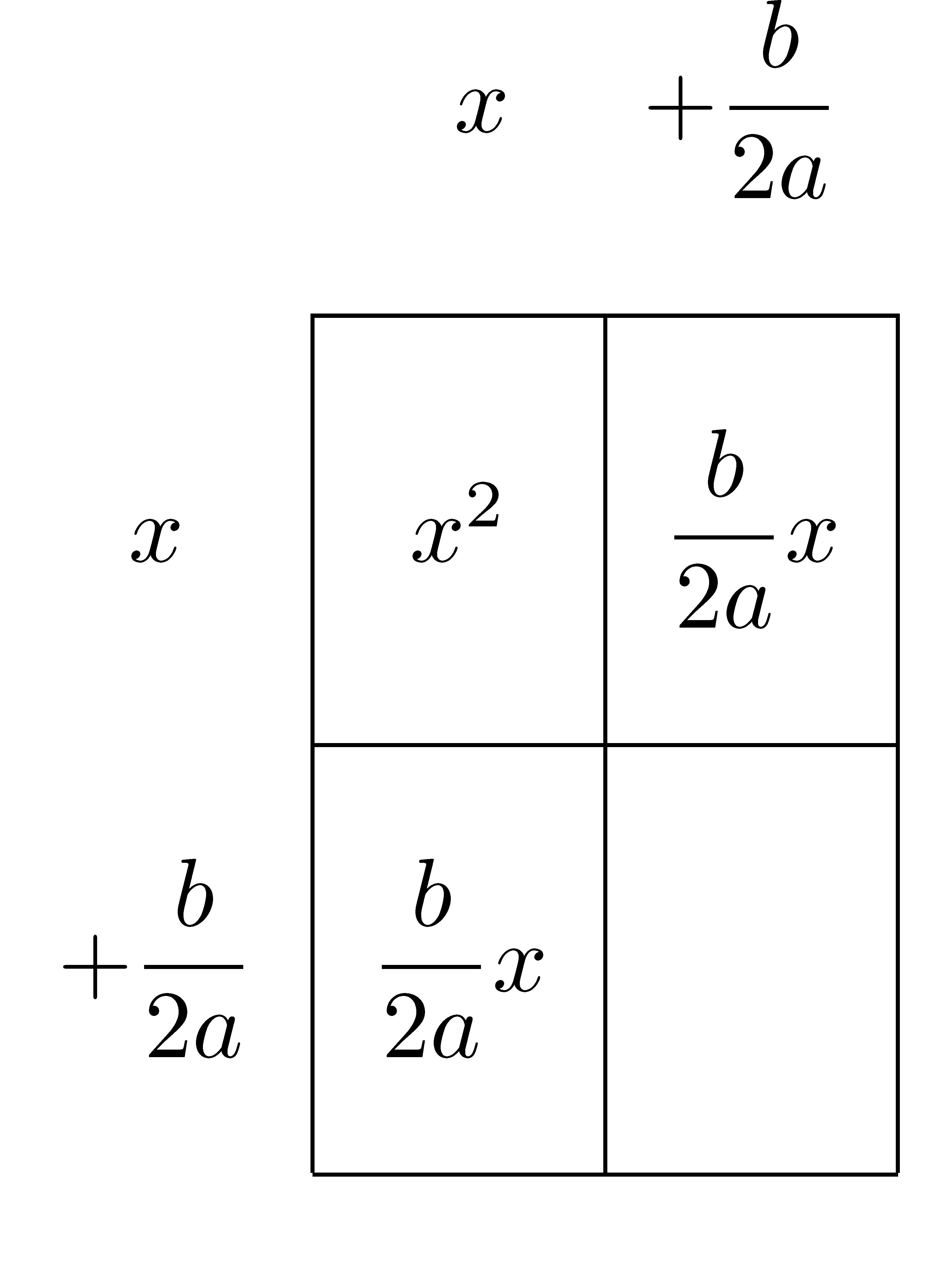
Figure 9.15: Completing the Square: Area Model
Then we see that the area needed to complete the square is \(\frac{b^2}{4a^2}\) and so we adjust the polynomial accordingly to \[f(x) = a \left( x^2 +\frac{b}{a}x + \frac{b^2}{4a^2} - \frac{b^2}{4a^2} \right) + c.\] We are now able to distribute the \(a\) through the parenthesis to get \[f(x) = a \left( x^2 +\frac{b}{a}x + \frac{b^2}{4a^2} \right)- \frac{b^2}{4a} + c\] and we see that the expression inside of the parenthesis is the area of the square. Hence, \[f(x) = a \left(x+\frac{b}{2a} \right)^2- \frac{b^2}{4a} + c.\]
Therefore, we can write all quadratic polynomials in the form \[f(x) = a \left(x+\frac{b}{2a} \right)^2- \frac{b^2-4ac}{4a}.\]
We can also look at quadratic polynomials from the perspective of transformations of the graph. Beginning with \(f(x)=x^2\), we can see that the family of functions generated from this function are of the form \[h(x)= a (x-h)^2 + k\] which we will call the vertex form of the quadratic function, with the vertex being \((h,k)\). Equating this with the prior expression we see that all quadratic polynomials can be written in this way and that the vertex of a polynomial of the form \[f(x)=ax^2+bx+c\] is at the point \[\left(-\frac{b}{2a}, - \frac{b^2-4ac}{4a}\right).\]
We also see from properties of the transformations of the graph that if \(a>0\) the parabola opens up and if \(a<0\) the parabola opens down. Thus the range of the function \(f(x)=ax^2+bx+c\) is
\[\left[-\frac{b^2-4ac}{4a}, \infty \right) \mbox{ if } a>0 \quad \mbox{and} \quad \left(-\infty, -\frac{b^2-4ac}{4a}\right] \mbox{ if } a<0.\]
Related Content Standards
- (HSA.SSE.3) Choose and produce an equivalent form of an expression to reveal and explain properties of the quantity represented by the expression.
- Complete the square in a quadratic expression to reveal the maximum or minimum value of the function it defines.
9.5.2 Factoring
In addition to the standard form of \(f(x)=ax^2+bx+c\) and the vertex form of \(f(x)=a(x-h)^2+k\), it is useful to write quadratic functions in their factored form of \(f(x)=(x-d_1)(x-d_2)\) as this form helps to determine the horizontal intercepts of the graph of the function, and the zeros of the polynomial.
To move from the standard form to the factored form, one uses the vertex form of \[f(x) = a \left(x+\frac{b}{2a} \right)^2- \frac{b^2-4ac}{4a}\] and then find the values of \(x\) for which the function is equal to zero. These points are the values \(d\) such that \[a\left(d+\frac{b}{2a} \right)^2- \frac{b^2-4ac}{4a}=0.\] Using some algebraic properties we can rewrite this equation as \[\left(d+\frac{b}{2a} \right)^2= \frac{b^2-4ac}{4a^2}.\] We then see that there are two values for \(d\) that make this equation true. \[d_1 = \frac{-b+\sqrt{b^2-4ac}}{2a} \quad \mbox{and} \quad d_2 = \frac{-b-\sqrt{b^2-4ac}}{2a}.\]
Therefore, the factored form of the quadratic can be written as \[f(x) = \left( x- \frac{-b+\sqrt{b^2-4ac}}{2a}\right) \left(x- \frac{-b-\sqrt{b^2-4ac}}{2a}\right).\]
This will look very familiar as the quadratic equation.
Related Content Standards
- (HSA.SSE.3) Choose and produce an equivalent form of an expression to reveal and explain properties of the quantity represented by the expression.
- Factor a quadratic expression to reveal the zeros of the function it defines.
- (HSN.CN.7) Solve quadratic equations with real coefficients that have complex solutions.
9.5.2.1 Difference of Squares
While the quadratic formula works every time for factoring a quadratic polynomial, there are a couple polynomial identities that are very useful when factoring specific types of quadratics. The first is when we see a difference of squares. \[x^2-b^2= (x-b)(x+b)\] This difference of squares can also be used to factor \(x^4-16\) as \((x^2-4)(x^2+4)\). We can then rewrite this to find more differences of squares so that \[\begin{align*} x^4-16 &= (x^2-4)(x^2+4) = (x^2-4)(x^2- (-4)) \\ &= (x-2)(x+2)(x-2i)(x+2i). \end{align*}\] Another quadratic form that creates a simpler factorization is a perfect square. \[x^2+2ax+a^2 = (x+a)^2\] This can be recognized when the absolute value of the middle term of a quadratic is twice the product of the square roots of the other two terms. Some examples of uses include \(4x^2+12x +9\) or \(12y^2-8\sqrt{3} y +4\).
Related Content Standards
- (HSN.CN.8) Extend polynomial identities to the complex numbers.
9.5.3 Inverse Function
We notice that a quadratic polynomial does not have an inverse. However, if we restrict the domain of the quadratic polynomial to an interval on which it is monotonic, we can find an inverse. So if we look at the function \[f:[0,\infty) \rightarrow [0,\infty) \: \mbox{ with } \: f(x)=x^2\] we see that \(f\) is a bijection. We define the inverse function as \[g:[0,\infty) \rightarrow [0,\infty) \: \mbox{ with } \: g(x)=\sqrt{x}.\] We will look at this process of restricting the domain in order to find the inverse function in more detail in the section on trigonometric functions.
9.5.4 Exercises
Let \(m\) and \(n\) be the zeros of the function \(f(x)=ax^2+bx+c\).
- Find a formula for \(m+n\) in terms of \(a\), \(b\), and \(c\).
- Find a formula for \(m^2+n^2\) in terms of \(a\), \(b\), and \(c\).
- Find a formula for \(m^3+n^3\) in terms of \(a\), \(b\), and \(c\).
Given \(f(x)=-ax^2+2ahx-ah^2+k\), find the domain and range of \(f(x)\) where \(a>0\), \(h>0\), and \(k>0\).
Given \((k-1)x^2 + kx+1=0\), where \(-1\) is one solution, what is the other solution?
Let \(y=f(x)\) be a parabola with vertex \((4,1)\) that passes through the point \((3,-7)\).
What are the domain and range of \(f(x)\)? Explain how you found your answers based on just the vertex and the point given.
What is the equation of this parabola in vertex form? Show your work algebraically. Explain how you used the points indicated on the graph to determine the equation.
Let \(d(n)\) stand for the number of diagonals of a polygon of \(n\) sides. Here is a table of values of \(d(n)\).
Table 9.2: \(n\) \(d(n)\) 3 0 4 2 5 5 6 9 7 14 8 20 9 27 10 35 11 44 - Use the table of values to find a polynomial formula for \(d(n)\) in terms of \(n\).
- Give a geometric argument to show that your formula is true for all \(n\).
The top and bottom margins of a poster are each 6 cm and the side margins are each 4 cm. If the area of the printed material on the poster is fixed at 384 cm2, find the dimensions of the poster with the smallest area.