10.7 Circle Theorems
In Book IV of Euclid’s Elements (Heath, 1908b), Euclid returns to constructions involving regular polygons and circles. Before we look at these constructions we need to first define some terms and prove some basic properties of circles.
::: {.definition} A chord is a line segment whose endpoints lie on the circle. :::
Definition 10.12 An inscribed angle is an angle formed by two chords in a circle which have a common endpoint. This common endpoint forms the vertex of the inscribed angle. The other two endpoints define what we call an intercepted arc on the circle.
Definition 10.13 A central angle is any angle whose vertex is located at the center of a circle. A central angle necessarily passes through two points on the circle, which in turn divide the circle into two arcs: a major arc and a minor arc. The minor arc is the smaller of the two arcs, while the major arc is the bigger. We define the arc angle to be the measure of the central angle which intercepts it.
The inscribed angle and central angle related to the same arc are related in the following way.
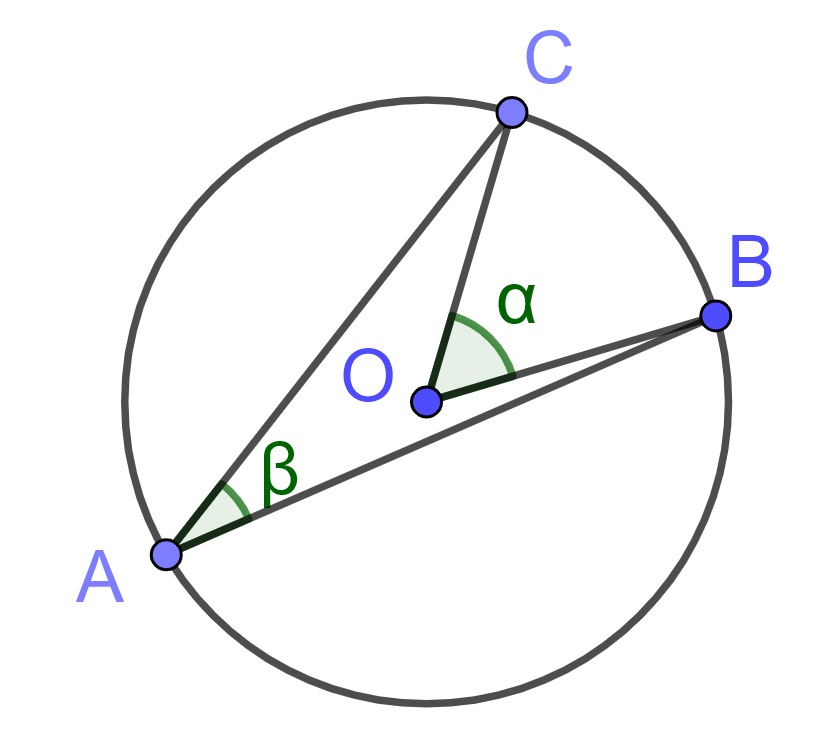
Theorem 10.22 In a circle, the measure of an inscribed angle is half the measure of the central angle with the same intercepted arc.
Proof. Let \(O\) be the center of a circle with unknown radius. Let \(A\) be the common end point of chords \(AB\) and \(AC\) on the circle and let \(\alpha\) be the measure of \(\angle COB\) and \(\beta\) be the measure of \(\angle CAB\).
\(OB\) and \(OC\) are the same length because they are both radii of the same circle. Therefore, \(\triangle BOC\) is isosceles and \(\angle OCB\) and \(\angle OBC\) are equal and both equal \(\frac{180^\circ - \alpha}{2}\).
We also see that \(\triangle OAC\) is isosceles and we can let \(x\) be the measure of angles \(\angle OAC\) and \(\angle OCA\). Similarly \(\triangle OBA\) is isosceles and we can let \(y\) be the measure of the angles \(\angle OBA\) and \(\angle OAB\).
Then \(\beta = x+y\), the measure of \(\angle ACB\) is \(x+\frac{180^\circ - \alpha}{2}\) and the measure of \(\angle ABC\) is \(y+\frac{180^\circ - \alpha}{2}\). Since the sum of the angles of a triangle equal two right angles, \[(x+y) + \left(x+\frac{180^\circ - \alpha}{2}\right) + \left(y+\frac{180^\circ - \alpha}{2}\right) = 180^\circ.\] Reordering the terms leads to \(2(x+y) = \alpha\), and since \(\beta=x+y\), we have our result that the inscribed angle is half of the central angle.
If the central angle is a straight line forming a diameter to the circle, the central angle equals two right angles and we have the following.
Theorem 10.23 Any angle inscribed in a semi-circle is a right angle.
We are now ready to return to the constructions of Euclid, which we will leave as exercises.
Related Content Standards
- (HSG.CO.13) Construct an equilateral triangle, a square, and a regular hexagon inscribed in a circle.
10.7.1 Exercises
Construct the inscribed circle of a triangle, and prove that it is such.
Construct the circumscribed circle of a triangle, and prove that it is such.
Construct a tangent line from a point outside a given circle to the circle, and prove that it is such.
Construct an equilateral triangle inscribed in a circle, and prove that it is such.
Construct a square inscribed in a circle, and prove that it is such.
Construct a regular hexagon inscribed in a circle, and prove that it is such.