13.3 Translations
Our first type of isometry that we discuss are translations that involve a shifting of the plane, without any turning. If we use a sheet of paper to represent the plane, these transformations are a sliding of the paper without changing the orientation of the paper. Intuitively we see that this really does not change the plane at all, it just changes our perspective of the plane.
13.3.1 Synthetic Plane
Definition 13.10 Given a segment \(\overline{AB}\), we define the translation \(T_{\overline{AB}}\) for every point \(C\) by \(C'=T_{\overline{AB}}(C)\) is the unique point in the plane so that \(\overline{CC'}\) has the same length as \(\overline{AB}\) and is parallel to \(\overline{AB}\).
So if we start with a segment \(\overline{AB}\) and a point \(C\), we can find the midpoint of the segment \(\overline{BC}\) and label it as \(D\). Then we find the point on the line \(\overleftrightarrow{AD}\) that is the same distance from \(D\) as \(A\), and label the point \(C'\).
If \(C\) was not on the line \(\overleftrightarrow{AB}\), \(\overline{BC}\) and \(\overline{AC'}\) bisect each other, and so \(ABC'C\) is a parallelogram and so \(\overline{CC'}\) is the same length as, and parallel to, \(\overline{AB}\).
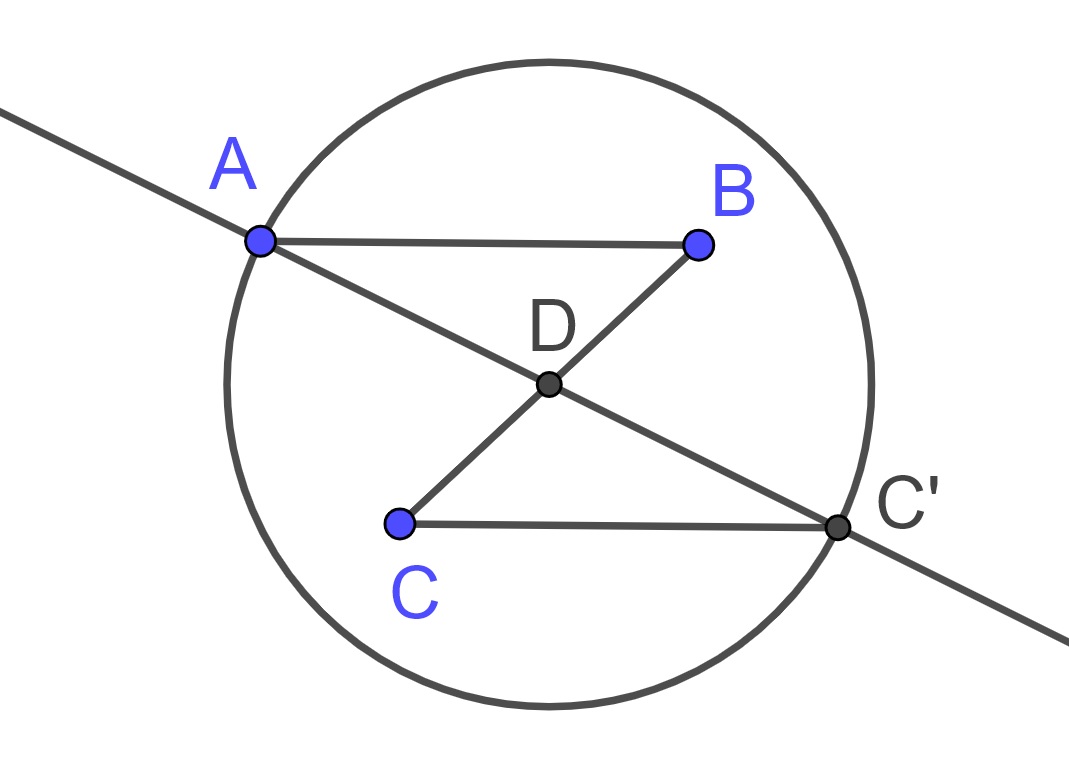
If \(C\) was on the line \(\overline{AB}\), we see that \(C'\) is also on the same line and the length of \(\overline{CC'}\) is the same as \(\overline{AB}\). So we see that the translations on the synthetic plane are constructible.
To prove that these translations are isometries we let \(C\) and \(D\) be any two points of the plane and we let \(C'=T_{\overline{AB}}(C)\) and \(D'=T_{\overline{AB}}(D)\). Since \(\overline{CC'}\) and \(\overline{DD'}\) are two segments of the same length and are parallel to one another, properties of parallelograms determine that \(CDD'C'\) is a parallelogram and \(\overline{CD}\) is the same length as \(\overline{C'D'}\). So the translation maintains the distance between points on the plane.
Related Content Standards
- (HSG.CO.4) Develop definitions of rotations, reflections, and translations in terms of angles, circles, perpendicular lines, parallel lines, and line segments.
13.3.2 Cartesian Plane and Vector Space
When we add the coordinates to the plane, the definition and properties of the translation become easier to describe due to the increased amount of information provided by the Cartesian coordinate system. In particular, since any translation can be viewed as a combination of horizontal and vertical translations we see that a translation of a set length in a certain direction is defined by these two simpler translations.
Definition 13.11 Given a point \((h,k)\in \mathbb{R}^2\), we define \(T_{(h,k)}\) by \[T_{(h,k)} \left( (x,y)\right) = (x+h,y+k).\]
A translation corresponding to a line segment between the points \(A=(a_1,a_2)\) and \(B=(b_1,b_2)\) in this perspective corresponds to the point \((h,k)\), where \(h=b_1-a_1\) and \(k=b_2-a_2\). We can also show that translations are isometries using this perspective by letting \(C=(c_1,c_2)\) and \(D=(d_1,d_2)\) be two points in \(\mathbb{R}^2\) and let \((h,k)\) be a point in \(\mathbb{R}^2\). Then
\[\begin{align*} d\left( T_{(h,k)}(C), T_{(h,k)}(D)\right) & = d\left( (c_1+h,c_2+k), (d_1+h,d_2+k)\right) \\ & = \sqrt{ \left( (d_1+h)-(c_1+h)\right)^2 + \left( (d_2+k)-(c_2+k)\right)^2 } \\ & = \sqrt{ (d_1-c_1)^2 + (d_2-c_2)^2 } = d\left(C,D\right) \end{align*}\] and so \(T_{(h,k)}\) maintains distances.
Using a basic understanding of vectors, the properties of translations in the Cartesian perspective translate very easily to the vector space perspective.
Definition 13.12 Given a vector \(\langle h,k\rangle\), we define \(T_{\langle h,k \rangle}\) by \[T_{\langle h,k \rangle} \left( \langle x,y\rangle \right) = \langle x,y \rangle + \langle h,k \rangle = \langle x+h,y+k\rangle.\]
13.3.3 Complex Plane
Complex numbers provide even more structure than \(\mathbb{R}^2\) and so the notation for translations is simplified.
Definition 13.13 Given a complex number \(b\in \mathbb{C}\), we define \(T_b\) by \[T_b(z) = z+b.\]
This additional structure provided by \(\mathbb{C}\) also simplifies the proof that translations are isometries, \[ \left| T_b(w)-T_b(z)\right| = \left|(w+b)-(z+b)\right| = |z-w|.\]
13.3.4 Compositions
Theorem 13.8 The composition of two translations is a translation.
Proof. Let \(T_b\) and \(T_c\) be two translations of \(\mathbb{C}\). Then \[T_b\circ T_c(z) = T_b(z+c) = (z+c)+b = z + (c+b) = T_{c+b}(z).\]
We can also see that the order of the translations does not matter.
13.3.5 Group of Translations
Theorem 13.9 Let \(T\) be the set of translations of the plane. Then with the operation of function composition, \((T,\circ)\) is a subgroup of \((I,\circ )\).
Proof. Since the composition of two translations is also a translation, \((T,\circ)\) is closed.
Since the identity function can be considered a translation, \(T_0(z)=z+0\), we see that \((T,\circ)\) has an identity.
Since for any \(b\in \mathbb{C}\), \(T_b \circ T_{-b} (z) = z-b+b=z\), we see that \(T_b\) is invertible and \(T_b^{-1} = T_{-b}\). So the inverse of any translation is also a translation.
Therefore, \((T,\circ)\) is a subgroup of \((I,\circ )\).
Recall from Section 7.1 that two groups, \((G,*)\) and \((G',\times)\), are isomorphic (‘equivalent’) if there is a bijection \(\phi: G \rightarrow G'\) such that \[\phi(a*b) = \phi(a)\times \phi(b)\] for all \(a,b\in G\).
If we let \(\phi:\mathbb{C} \rightarrow T\) be defined by \(\phi(b)=T_b\), we see that \[\phi(b+c) = T_{b+c} = T_b \circ T_c = \phi(b) \circ \phi(c),\] making \(\phi\) a group homomorphism. From the definition of translations on \(\mathbb{C}\) we can see that \(\phi\) is also a bijection. So we get the following theorem.
Theorem 13.10 The group \((T,\circ)\) is isomorphic to the group \((\mathbb{C},+)\).
13.3.6 Exercises
Let \(T\) be the translation by the vector \(\langle 1,3\rangle\).
- Write an algebraic representation for the translation from each of the four perspectives.
- Find the image of the circle \(C=\left\{ (x,y)\in \mathbb{R}^2 \: \vert \: (x-2)^2+(y+3)^2 =9\right\}\) under this translation.
- Let \(A=(1,2)\), \(B=(-2,3)\) and \(C=(0,0)\). Find the image of the triangle \(\triangle ABC\) under this translation.
Let \(z\in \mathbb{C}\). Why is \(T_{z+\overline{z}}\) a horizontal translation?
Let \(z\in \mathbb{C}\). Show that \(T_{z-\overline{z}}\) is a vertical translation.
Show that the set of horizontal translations with function composition forms a group and that the group is isomorphic to \((\mathbb{R},+)\).
We say that two translations, \(T_1\) and \(T_2\), are parallel if for any point \(A\), \(A\), \(T_1(A)\), and \(T_2(A)\) are co-linear. Assuming that \(T_1\) and \(T_2\) are parallel, answer the following questions.
- Let \(T_1(x,y)=(x+h_1,y+k_1)\) and \(T_2(x,y)=(x+h_2,y+k_2)\). Write a single algebraic equation that expresses the relationship between \(h_1\), \(h_2\), \(k_1\), and \(k_2\).
- Let \(T_1(z)=z+b_1\) and \(T_2(z)=z+b_2\). Write a single algebraic equation that expresses the relationship between \(b_1\) and \(b_2\). (Do not break the complex numbers up into their real and imaginary parts.)
Is \((T,\circ )\) a normal subgroup of \((I,\circ )\)? (Consider \(f^{-1} \circ T_d \circ f\) for all \(f\in I\).) If so, describe the elements of the factor group and determine if the factor group is isomorphic to another known group.