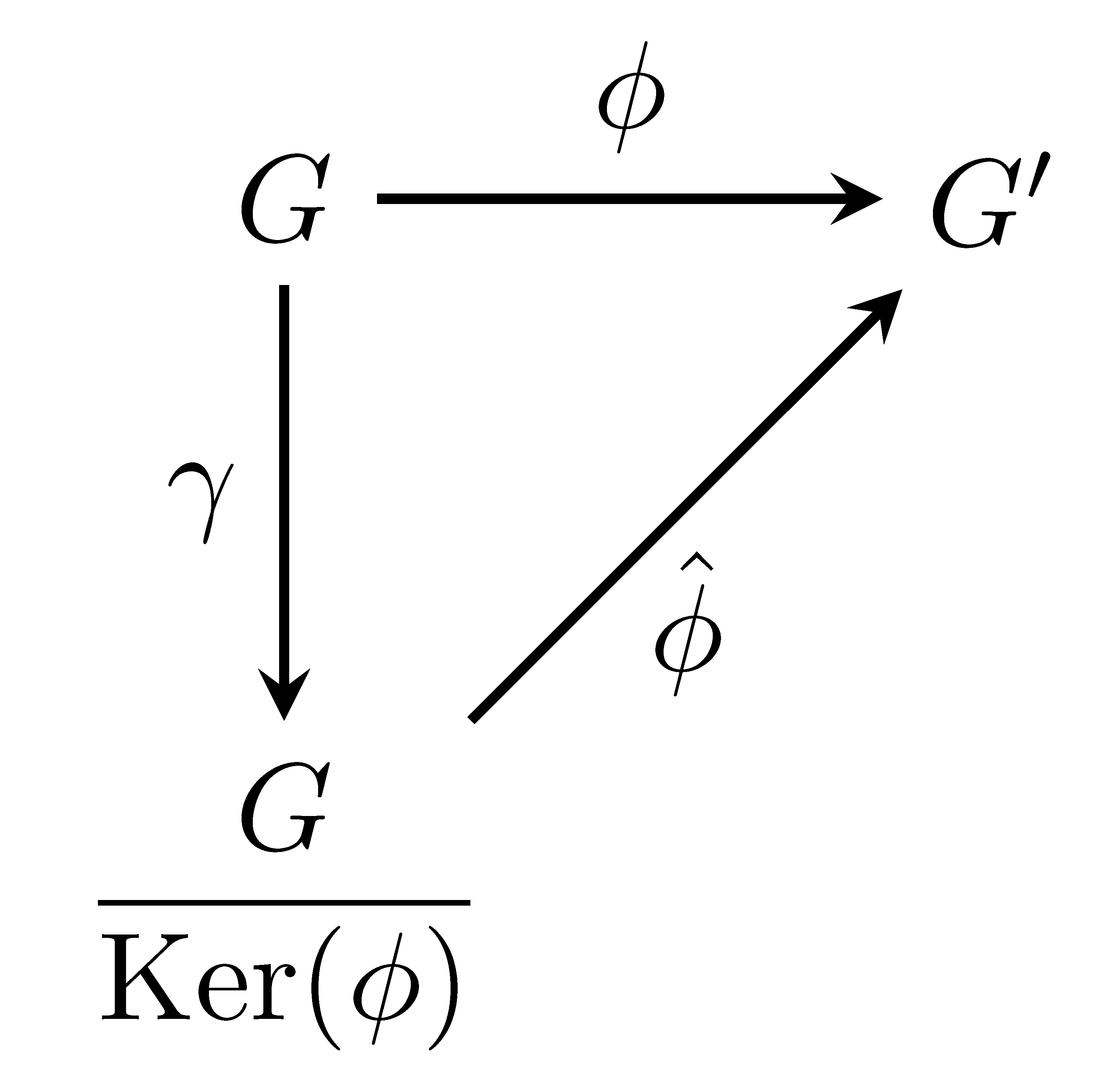12.3 Group Homomorphisms Revisited
Recall the following definition of group homomorphism and isomorphism.
Definition 12.5 A map, \(\phi\), from a group \((G,*)\) to a group \((G',\cdot)\) is called a homomorphism if \[ \phi(a*b)=\phi(a) \cdot \phi(b)\] for every \(a,b\in G\). If \(\phi\) is also a bijection, then we say that \(\phi\) is an isomorphism.
Now that we know when two groups are isomorphic to one another, we turn to looking at how “different” two groups are that are not isomorphic, but have a homomorphism between them by looking at the set of points of the domain that are mapped to the identity. This provides information about how far away the group homomorphism is from a one-to-one function .
Theorem 12.6 Let \(\phi: G \rightarrow G'\) be a group homomorphism. The set \(\left\{ a\in G : \phi(a)=e' \right\}\), where \(e'\) is the identity in \(G'\), is a subgroup of \(G\) and is called the kernel of \(\phi\), denoted by \(\mbox{Ker}(\phi)\).
Proof. Since \(\phi\) is a group homomorphism, if \(e\) is the identity in \(G\), \(\phi(a)=\phi(a*e)=\phi(a)*\phi(e)\) for all \(a\in G\). So \(\phi(e)\) is the identity in \(G'\). Therefore, \(e \in \mbox{Ker}(\phi)\).
If \(a,b \in \mbox{Ker}(\phi)\), then \[ \phi(a*b)=\phi(a) \cdot \phi(b) = e' \cdot e' = e' \] and so \(a*b \in \mbox{Ker}(\phi)\).
If \(a\in \mbox{Ker}(\phi)\), then \[\phi(a^{-1}) = \phi(a^{-1})\cdot e' = \phi(a^{-1})\cdot \phi(a) = \phi(a^{-1}*a) = \phi(e)=e'\] and so \(a^{-1}\in \mbox{Ker}(\phi)\).
Therefore, \(\mbox{Ker}(\phi)\) is a subgroup of \(G\).
Now that we know that the kernel of a group homomorphism is a subgroup, we prove that it is in fact a normal subgroup.
Theorem 12.7 If \(\phi:G \rightarrow G'\) is a group homomorphism, then \(\mbox{Ker}(\phi) \vartriangleleft G\).
Proof. By the previous theorem, we have proven that \(\mbox{Ker}(\phi)\) is a subgroup of \(G\). Thus it is sufficient to prove that \[g \mbox{Ker}(\phi)= \mbox{Ker}(\phi) g \quad \forall g\in G.\]
Let \(g\in G\) and let \(a \in \left\{ x \in G : \phi(x)= \phi(g) \right\}\). Then since \(\phi(a)=\phi(g)\), we can multiply both sides of the equation by \(\phi(g)^{-1}\) on the left (respectively right) and we have that \[\phi(g)^{-1} \phi(a) = e' \quad \left(\mbox{respectively } \phi(a) \phi(g)^{-1} =e' \right).\] Since \(\phi\) is a homomorphism, this is equivalent to \[\phi(g^{-1} a) =e' \quad \left( \mbox{repectively } \phi( a g^{-1}) =e' \right) .\] So \(g^{-1}a\) and \(a g^{-1}\) are elements of \(\mbox{Ker}(\phi)\). Therefore, since \(a= g (g^{-1}a)\) and \(a= (a g^{-1})g\), we have that \(a \in g \mbox{Ker}(\phi)\) and \(a \in \mbox{Ker}(\phi) g\) and so \[\left\{ x \in G : \phi(x)= \phi(g) \right\} \subseteq g \mbox{Ker}(\phi) \quad \mbox{and} \quad \left\{ x \in G : \phi(x)= \phi(g) \right\} \subseteq \mbox{Ker}(\phi) g\]
Let \(a \in g \mbox{Ker}(\phi)\). Then there exists a \(b\in \mbox{Ker}(\phi)\) such that \(a=gb\). Thus \(b=g^{-1}a\) and so \(e'=\phi(b) = \phi(g^{-1} a) = \phi(g)^{-1} \phi(a)\) and so \(\phi(a)=\phi(g)\). Similarly if \(a \in \mbox{Ker}(\phi)\), then \(\phi(a)=\phi(g)\).
Therefore, \[g \mbox{Ker}(\phi) = \left\{ x \in G : \phi(x)= \phi(g) \right\} = \mbox{Ker}(\phi) g\] and so \(\mbox{Ker}(\phi) \vartriangleleft G\).
So we have shown that for every homomorphism, the kernel of the homomorphism is a normal subgroup. Alternatively, if we start with a normal subgroup, we can create a homomorphism for which the normal subgroup is equal to the kernel.
Theorem 12.8 Let \(G\) be a group and let \(N\) be a normal subgroup of \(G\). Then the function \(\gamma: G \rightarrow \frac{G}{N}\) defined by \(\gamma(g)=gN\) is a group homomorphism and \(\mbox{Ker}(\gamma) = N\).
Proof. Because \[\gamma(g_1 g_2) = (g_1 g_2) N = \left(g_1 N\right) \left(g_2 N\right) = \gamma(g_1) \gamma(g_2)\] we know that \(\gamma\) is a group homomorphism.
Since the only elements \(g \in G\) such that \(gN=N\) are the elements of \(N\), we have that \(\mbox{Ker}(\gamma)=N\).
This means that there is a strong relationship between normal subgroups and kernels of group homomorphisms. This leads us to one of the most important theorems in basic group theory.
Theorem 12.9 (Fundamental Homomorphism Theorem) Let \(\phi: G \rightarrow G'\) be a group homomorphism with kernel \(\mbox{Ker}(\phi)\). Then \(\phi(G)\) is a group and the map \[\hat{\phi} : \frac{G}{\mbox{Ker}(\phi)} \rightarrow \phi(G)\] defined by \(\hat{\phi} \left( a \mbox{Ker}(\phi)\right) = \phi(a)\) is an isomorphism.
Proof. We first need to prove that \(\phi(G)\) is a subgroup of \(G'\). Since \(\phi\) is a homomorphism, \(\phi(G)\) is closed under the binary operation. From Theorems 7.3 and 7.4 we have that the identity of \(G'\) is in \(\phi(G)\) and if \(\phi(a)\in \phi(G)\) then \(\phi(a)^{-1}\in \phi(G)\). So \(\phi(G)\) is a subgroup of \(G'\).
If \(a\) and \(a'\) are two elements of \(G\) such that \(a \mbox{Ker}(\phi) = a' \mbox{Ker}(\phi)\), we know that there are elements \(b\) and \(b'\) in \(\mbox{Ker}(\phi)\) such that \(a b = a' b'\). So \(a'= ab (b')^{-1}\) and \[\phi(a') = \phi(ab (b')^{-1}) = \phi(a) \phi(b) \phi(b')^{-1} = \phi(a)\] so \(\hat{\phi}\) is well-defined.
If \(a \mbox{Ker}(\phi)\) and \(b \mbox{Ker}(\phi)\) then \[\hat{\phi} \left( \left(a \mbox{Ker}(\phi) \right) \left((b \mbox{Ker}(\phi)\right) \right) = \hat{\phi} \left( (ab) \mbox{Ker}(\phi) \right) = \phi(ab) = \phi(a) \phi(b) = \hat{\phi}\left( a \mbox{Ker}(\phi)\right) \hat{\phi} \left(b \mbox{Ker}(\phi)\right)\] and so \(\hat{\phi}\) is a homomorphism.
If \(a \mbox{Ker}(\phi)\) is in the kernel of \(\hat{\phi}\), we know that \(\phi(a)\) is the identity of \(G'\) and so \(a\in \mbox{Ker}(\phi)\). This implies that \(a \mbox{Ker}(\phi)= \mbox{Ker}(\phi)\) and so \(\mbox{Ker}(\hat{\phi}) = \mbox{Ker}(\phi)\) and so \(\hat{\phi}\) is one-to-one. By the definition of \(\phi(G)\) we know that \(\hat{\phi}\) is onto and so is a bijection.
Therefore, \(\hat{\phi}\) is an isomorphism.
The prior two theorems can be summarized in the following commutative diagram.