9.3 Linear and Exponential Functions

9.3.1 Linear Functions

The first parent function that we will study is the identity function $f(x)=x$. With this function, we see that horizontal and vertical dilations are connected in that $f(ax)=a f(x) = ax$, and that these function describe proportional relationships between two variables. These proportional relationships are part of the core of the middle school mathematics curriculum, along with much of the physical science curriculum.

Related Content Standards

(6.RP.1) Understand the concept of a ratio and use ratio language to describe a ratio relationship between two quantities.
(6.RP.3) Use ratio and rate reasoning to solve real-world and mathematical problems.
(7.RP.2) Recognize and represent proportional relationships between quantities.
(8.EE.5) Graph proportional relationships, interpreting the unit rate as the slope of the graph.

While a direct proportional relationship fits some situations very well, such as Hooke’s law that the force needed to compress a spring by a distance is directly proportional to that distance, many others can be modeled by a proportional relationship near certain values. In fact, one of the foundations of calculus is that most functions that we use in modeling can locally be approximated by a proportional relationship. However, to model these proportional relationships we often need to translate the function to a point on the function. Such a translation gives us that for any ‘differentiable’ function, $f$, near a point $x=a$ we can approximate $f$ by \[f(x) \approx f'(a)(x-a) + f(a).\] As such, we will study the family of linear functions of the form \[f(x)=m(x-h)+k,\] often described as the point-slope form of a line with slope $m$ through the point $(h,k)$. These functions can also be written in a slope intercept form, $f(x)=mx+b$ where $b=k-mh$.

If $f(x)=mx+b$, then we can see that the domain and range of the function is all of the real numbers. If $m>0$ the function is strictly increasing, while if $m<0$ it is strictly decreasing. As such, the function has no extrema.

We also know that since linear functions are monotonic, they are invertible. If $y=f(x)=mx+b$, the inverse of $f$ is $x=f^{-1}(y)= \frac{1}{m} y-\frac{b}{m}$.

9.3.2 Exponential Functions

In Section 7.2, we found a strong relationship between linear functions and exponential functions with the additive relationship of linear functions corresponding with the multiplicative relationship of exponential functions. In the case of exponential functions we will have our parent function be the function $f(x)=e^x$, making the family of exponential functions to be written in the form \[a f(b(x-h))+k = a e^{b(x-h)}+k = (ae^{-bh}) \cdot e^{bx} +k\] which means that we can generate all possibilities with functions of the form $g(x)=a e^{bx} + k$

When introducing exponential functions in middle school, the base is usually either $2$ or $10$ since students have not yet been introduced to $e$, but we can see that each different base is actually a horizontal dilation of the function with base $e$.

We saw in Section 4.5 that if $b>0$ and $x<y$, then $e^b>1$ and $e^{bx}<e^{by}$, making $e^{bx}$ a strictly increasing function. Similarly if $b<0$, $e^{bx}$ is a strictly decreasing function. So we have the following possible shapes for functions of the form $g(x)=ae^{bx}$.

Figure 9.11: Graphs of Exponential Functions

We can see that with each of these cases that the function is monotonic and the range is either $(0,\infty)$ or $(-\infty,0)$, depending on the sign of $a$. If we perform a vertical translation to acheive the entire family of exponential functions then we see that we have the following properties for $f(x) = a e^{bx} +k$:

The domain is $\mathbb{R}$ and the range is $(k,\infty)$ if $a>0$ and $(-\infty,k)$ if $a<0$.
The function is strictly monotonic.
If $b>0$, then $e^b>1$, $f(x)\rightarrow k$ as $x\rightarrow -\infty$, and $f(x) \rightarrow \pm \infty$ as $x\rightarrow \infty$ (depending on the sign of $a$). These functions model exponential growth.
If $b<0$, then $0<e^b<1$, $f(x)\rightarrow k$ as $x \rightarrow \infty$, and $f(x) \rightarrow \pm \infty$ as $x\rightarrow -\infty$ (depending on the sign of $a$). These functions model exponential decay.

Related Content Standards

(HSF.IF.8) Write a function defined by an expression in different but equivalent forms to reveal and explain different properties of the function.
1. Use the properties of exponents to interpret expressions for exponential functions. For example, identify percent rate of change in functions such as $y=(1.02)^t$, $y = (0.97)^t$, $y = (1.01)12^t$, $y = \frac{(1.2)^t}{10}$, and classify them as representing exponential growth or decay.

9.3.3 Logarithmic Functions

Since the exponential functions are monotonic, they are bijections onto their range. If we let $f(x)=e^x$, then we know that $f:\mathbb{R} \rightarrow (0,\infty)$ is a bijection. From Chapter 5 we know that there is a unique function $g:(0,\infty) \rightarrow \mathbb{R}$ that is also a bijection with $g(f(x))=x$ for all $x\in \mathbb{R}$ and $f(g(x))=x$ for all $x\in (0,\infty)$. We will call this function the natural logarithm and denote it by $\ln$.

We can then use properties of the exponential function to determine properties of the natural logarithm.

If $\alpha,\beta >0$, then there exist $a$ and $b$ so that $\alpha = e^a$ and $\beta = e^b$, and \[\ln (\alpha \beta) = \ln \left( e^a \cdot e^b\right) = \ln \left(e^{a+b}\right) = a+b = \ln (\alpha) + \ln (\beta). \] We also have that \[\ln \left(\frac{\alpha}{\beta}\right) = \ln \left( \frac{e^a}{e^b} \right) = \ln \left( e^{a-b} \right) = a-b = \ln(\alpha) - \ln(\beta).\]

If $\alpha>0$ and $x\in \mathbb{R}$, then there exists an $a\in \mathbb{R}$ such that $\alpha=e^a$. Then \[\ln \left(\alpha^x\right) = \ln \left( \left(e^a\right)^x\right) = \ln \left( e^{ax} \right) = ax = x \ln(\alpha).\]

Related Content Standards

(HSF.BF.5) Understand the inverse relationship between exponents and logarithms and use this relationship to solve problems involving logarithms and exponents.

Since $a^x$ ($a>0$) has the same properties as $e^x$ it also has an inverse function that we will call logarithm base $a$ and denote it by \[ \log_a: (0,\infty) \rightarrow \mathbb{R}.\] We can find the relationships between the various bases. If $y= \log_a(x)$, then $x=a^y$. We can evaluate both sides of the equation in the natural log function so that \[\ln(x) = \ln\left(a^y\right) = y \ln (a)\] and so \[\log_a(x) = \frac{\ln(x)}{\ln(a)}.\]

Using these properties together we are able to use logarithm functions to find equivalent equations to equations such as $a b^{ct}=d$. By inputing both sides of the equation into the $\ln$ function, we have that \[\ln(a) + (ct)\ln(b) = \ln (d).\] We can then find the equivalent equation of \[t= \frac{\ln(d)-\ln(a)}{c\ln(b)}.\]

Related Content Standards

(HSF.LE.4) For exponential models, express as a logarithm the solution to $a b^{ct}=d$ where $a$, $c$, and $d$ are numbers and the base $b$ is $2$, $10$, or $e$; evaluate the logarithm using technology.

9.3.4 Relationships between Linear and Exponential

Since linear functions have a constant additive rate of change and exponential functions have a constant multiplicative rate of change, it is important to recognize the types of situations that are more likely to be modeled with a linear function and which are more likely modeled with an exponential function.

Related Content Standards

(HSF.LE.1) Distinguish between situations that can be modeled with linear functions and with exponential functions.
1. Prove that linear functions grow by equal differences over equal intervals, and that exponential functions grow by equal factors over equal intervals.
2. Recognize situations in which one quantity changes at a constant rate per unit interval relative to another.
3. Recognize situations in which a quantity grows or decays by a constant percent rate per unit interval relative to another.

Some of the factors that point towards a linear model are adding a fixed amount over fixed intervals in the domain, such as adding $200 to a savings account every month. Factors that direct the model to be exponential is that the amount of growth would depend upon the current value, such as interest rates or cell division in biology.

When given a set of data, the function used to model the data sometimes depends upon the question being asked about the data. Consider the following population data for the State of Alabama¹.

\[\begin{array}{c|ccccc} \mbox{Year} & 1800 & 1850 & 1900 & 1950 & 2000 \\ \hline \mbox{Population} & 1,250 & 771,623 & 1,828,697 & 3,061,743 & 4,447,100 \\ \end{array}\]

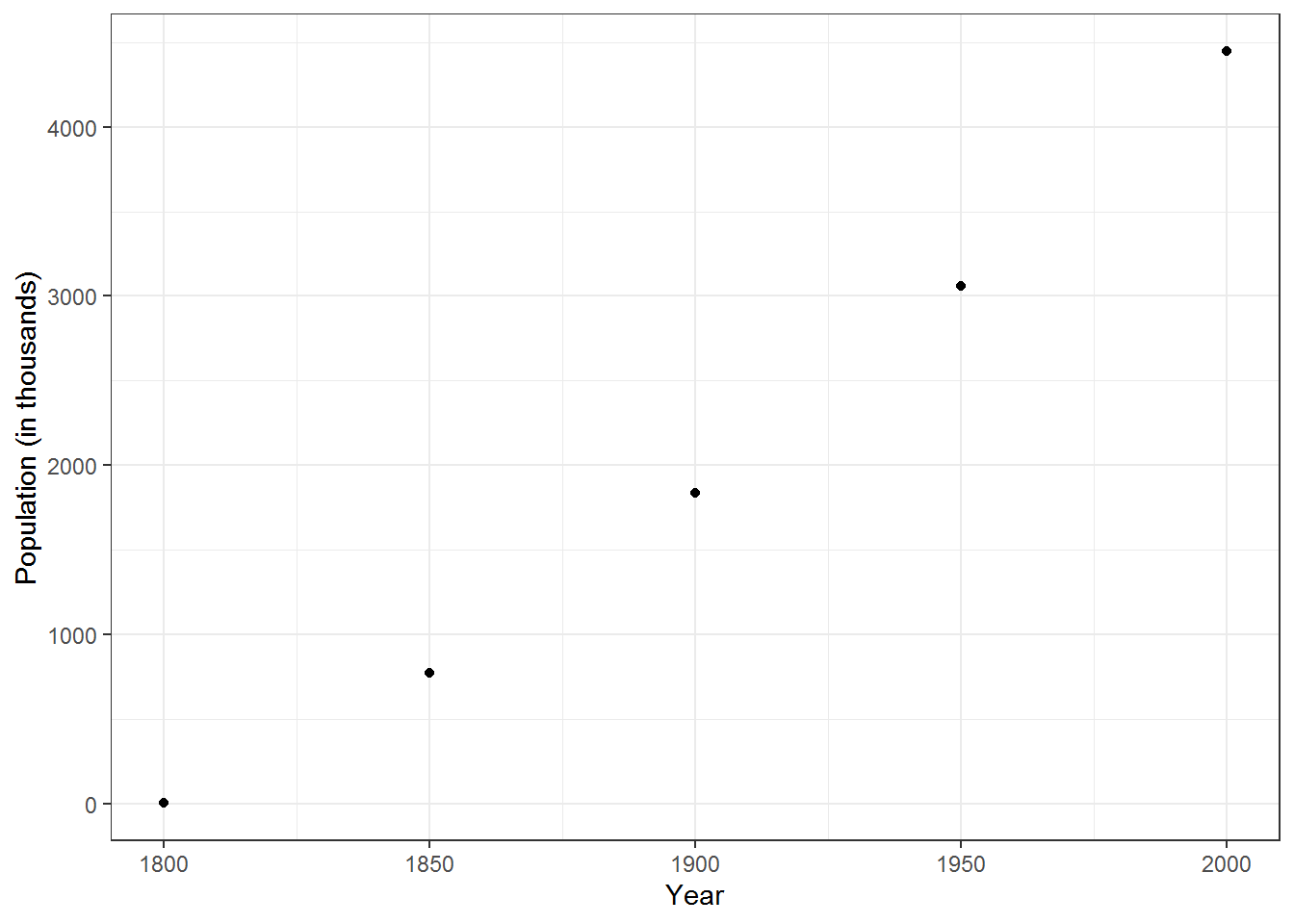
Figure 9.12: Population of Alabama

This data can be modeled using either a linear regression or an exponential regression. However, if you include the population in 1800 in the exponential regression, it estimates the population in 2050 to be nearly 100 million people (a highly unlikely number). If one only uses the data points from 1900, 1950, and 2000, the exponential model predicts a population of around 7 million in 2050. A linear model with all of the data points estimates the population in 2050 to be around 5.3 million people (a much more likely scenario).

If, however, you are wanting to estimate the population in years prior to 1800, the linear model becomes useless as it predicts a negative population. So for this type of question, an exponential function would be more useful.

9.3.5 Exercises

The salary scales in three school districts are as follows, for a teacher with a master’s degree:
- District $P$: $30,000 plus $1500 for each year of experience
- District $Q$: $30,000 plus $1750 for each year of experience
- District $R$: $28,000 plus $1750 for each year of experience
1. Give a formula for the salary in each district for a teacher with $n$ years of experience at the start of the school year.
2. Use your formulas to indicate the number of years experience teachers in Districts $P$ and $R$ when they earn the same salary.
3. Use your formulas to indicate the number of years experience teachers in Districts $P$ and $Q$ when they earn the same salary.
4. Use your formulas to indicate the number of years experience teachers in Districts $Q$ and $R$ when they earn the same salary.
5. If in District $T$, teachers earn a salary $S_T$ dollars plus $E_T$ dollars for each year of experience, and in District $U$, teachers earn a salary of $S_U$ dollars plus $E_U$ dollars for each year of experience, $S_T>S_U$, and $E_U>E_T$, how many years will it take District $U$ teachers to catch up to District $T$?
6. For each of the previous scenarios, at what value of $n$ will teachers in the two district have earned the same amount of total money during the previous $n$ years?

The following are winning times for the Men’s 100m dash at the Olympics.

Table 9.1: Race Times for Olympic Men’s 100m Dash
Year	Time (s)	Runner	Country
1948	10.30	Harrison Dillard	USA
1952	10.40	Lindy Remingino	USA
1956	10.50	Bobby Morrow	USA
1960	10.20	Armin Hary	Germany
1964	10.00	Bob Hayes	USA
1968	9.95	Jim Hines	USA
1972	10.14	Valery Borzov	USSR
1976	10.06	Hasely Crawford	Trinidad
1980	10.25	Allan Wells	Great Britain
1984	9.99	Carl Lewis	USA
1988	9.92	Carl Lewis	USA
1992	9.96	Linford Christie	Great Britain
1996	9.84	Donovan Bailey	Canada
2000	9.87	Maurice Greene	USA
2004	9.85	Justin Gatlin	USA
2008	9.69	Usain Bolt	Jamaica
2012	9.63	Usain Bolt	Jamaica
2016	9.81	Usain Bolt	Jamaica
2021	9.80	Marcell Jacobs	Italy

Find a mathematical function that models this behavior and use this function to predict the winning time in 2060. Give reasoning for your work, including the assumptions made for your models.

The number of bacteria in a certain population increases according to a continuous exponential growth model, with a growth rate parameter of $3.25\%$ per hour. How many hours does it take for the size of the sample to double?
LaVonda is choosing between 2 jobs. For Job A, she would earn $\$27,000$ the first year and each year after that she would get a raise of $\$3,000$. For Job B, she would earn $\$30,000$ the first year and each year after that she would get a raise of $4\%$ of the previous year’s salary.
1. What is the first year during which LaVonda’s salary for Job A would exceed that of Job B? Show your work, and explain the approach you used to find your answer.
2. Which year would the total amount earned since starting Job A first exceed the total amount earned since starting Job B? Show your work, and explain the approach you used to find your answer.
3. Using sequence and series formulas, what would LaVonda’s yearly salary and total amount of money earned be after 20 years at Job A? What would her yearly salary and total amount of money earned be after 20 years at Job B?
4. What recommendations would you provide for LaVonda?
A business owner spent $500 on start-up fees to produce and sell candles. Each candle costs an additional $3.00 to produce. What is the minimum number of candles that the owner must produce for the average cost per candle to be less than $3.75?

https://en.wikipedia.org/wiki/Demographics_of_Alabama, retrieved 6/25/2020↩︎