13.7 Group of Isometries
Now that we know that every isometry is a translation, rotation, reflection, or glide-reflection, we will look at this set of isometries more deeply and see how they all fit together.
Related Content Standards
- (HSG.CO.5) Given a geometric figure and a rotation, reflection, or translation, draw the transformed figure using, e.g., graph paper, tracing paper, or geometry software. Specify a sequence of transformations that will carry a given figure onto another.
- (HSG.CO.6) Use geometric descriptions of rigid motions to transform figures and to predict the effect of a given rigid motion on a given figure; given two figures, use the definition of congruence in terms of rigid motions to decide if they are congruent.
We will call the translations and rotations orientation preserving because they preserve the order of the vertices of a triangle when viewed in a clockwise direction. The reflections and glide-reflections, on the other hand, change the order of the vertices and so we call these isometries orientation reversing.
Theorem 13.21 (Three-Reflection Theorem) Every isometry can be written as a composition of at most three reflections.
Proof. Let \(f\) be an isometry. Then \(f\) is a translation, rotation, reflection, or glide-reflection.
If \(f\) is a translation that takes a point \(A\) to a point \(B\), then we can find the midpoint of \(\overline{AB}\) and call that point \(C\). We can then construct lines \(m\) and \(n\) through \(A\) and \(C\), respectively, so that \(m\) and \(n\) are perpendicular to \(\overleftrightarrow{AB}\). Then \(f=r_n \circ r_m\) and so can be written as a composition of two reflections.
If \(f\) is a rotation through the point \(C=(h,k)\) with an angle of \(\theta\), we can use the Cartesian perspective and let \(m\) be the line \(y=k\) and let \(n\) be the line \(y= \tan\left( \frac{\theta}{2}\right) (x-h) +k\). Then \(f= r_n \circ r_m\) and so can be written as a composition of two reflections.
Any reflection is already written as a composition of a reflection.
Since glide-reflections are a composition of a reflection and a translation, and since translations can be written as a composition of two reflections, glide-reflections can be written as a composition of three reflections.
From the proof above, we see that transformations that can be written as an odd number of reflections are orientation reversing, while those that can be written as an even number of reflections are orientation preserving. So, in a way, the orientation of the isometry is similar to a number being positive or negative.
When looking at the complex plane representation of the isometries, we see that the orientation preserving isometries are of the form \(f(z)=az+b\) and the orientation reversing isometries are of the form \(f(z)=a\overline{z}+b\). We will use this information to see how the behavior of an isometry on three distinct points determines the isometry.
Theorem 13.22 (Three Point Theorem) Let \(A\), \(B\), and \(C\) be three points in the plane that are not co-linear. Then any isometry, \(f\), is determined by the locations of \(f(A)\), \(f(B)\), and \(f(C)\).
Proof. We will let \(f\) be an isometry. We will use the perspective of the complex plane and let \(z_1\), \(z_2\), and \(z_3\) be three points that are not co-linear. Then we set \(w_1=f(z_1)\), \(w_2=f(z_2)\), and \(w_3=f(z_3)\).
In order to determine the orientation of the isometry we will use properties of the angles between the segments connecting the corresponding complex numbers. We can set \(z_1\) and \(w_1\) as our points of reference and then look at the relationship of the other points to these. We can measure the angle from \(z_2-z_1\) to \(z_3-z_1\) as \[\mbox{arg}(z_3-z_1)-\mbox{arg}(z_2-z_1) = \mbox{arg}\left(\frac{z_3-z_1}{z_2-z_1}\right).\] Similarly, the angle from \(w_2-w_1\) to \(w_3-w_1\) is \[\mbox{arg} \left( \frac{w_3-w_1}{w_2-w_1}\right).\] If these arguments are the same, then the isometry is orientation preserving and if they are additive inverses of each other the isometry is orientation reversing. This can most easily be checked by comparing the ratios \[\frac{w_3-w_1}{w_2-w_1} \quad \mbox{and} \quad \frac{z_3-z_1}{z_2-z_1}.\] If the ratios are equal, then the isometry is orientation preserving. If the ratios are complex conjugates of each other the isometry is orientation reversing.
Once we have determined if the isometry is orientation preserving or orientation reversing we can see how the equation of the isometry is determined.
If \(f\) is orientation preserving, \(f(z)=az+b\) for some \(a,b\in \mathbb{C}\) with \(|a|=1\). Using the three points we have the following system of equations \[\begin{matrix} w_1=a z_1 + b \\ w_2=a z_2+b \\ w_3=a z_3+b \end{matrix}\] Using the first two equations we can determine that \[a=\frac{w_2-w_1}{z_2-z_1}.\] Then from the third point we see that \[f(z) = \frac{w_2-w_1}{z_2-z_1} (z-z_3) + w_3.\]
If \(f\) is orientation reversing, \(f(z)=a\overline{z}+b\) for some \(a,b\in \mathbb{C}\) with \(|a|=1\). Then following a similar process to the one above we see that \[f(z)= \frac{w_2-w_1}{\overline{(z_2-z_1)}} \overline{(z-z_3)} + w_3.\]
13.7.1 Fixed Points
For a function \(f:A\rightarrow A\), we say that \(c\in A\) is a fixed point of \(f\) if \(f(c)=c\). This property of fixed points is a way of describing different functions and can help us classify functions. In particular, the isometries of the plane have different numbers of fixed points.
13.7.2 Exercises
Classify the transformation \(f\) as one of the four types of isometries from its formula in the complex plane.
- \(\displaystyle{f(z)=\left( \frac{1}{\sqrt{2}} - \frac{i}{\sqrt{2}} \right) z +i}\)
- \(\displaystyle{f(z)=\left( \frac{1}{\sqrt{2}} - \frac{i}{\sqrt{2}} \right) \overline{z} +i}\)
- \(\displaystyle{f(z)=i\overline{z}-2}\)
- \(\displaystyle{f(z)=z-2+i}\)
Identify the following compositions where \(ABCD\) is the square below. (You may need to draw additional points.)
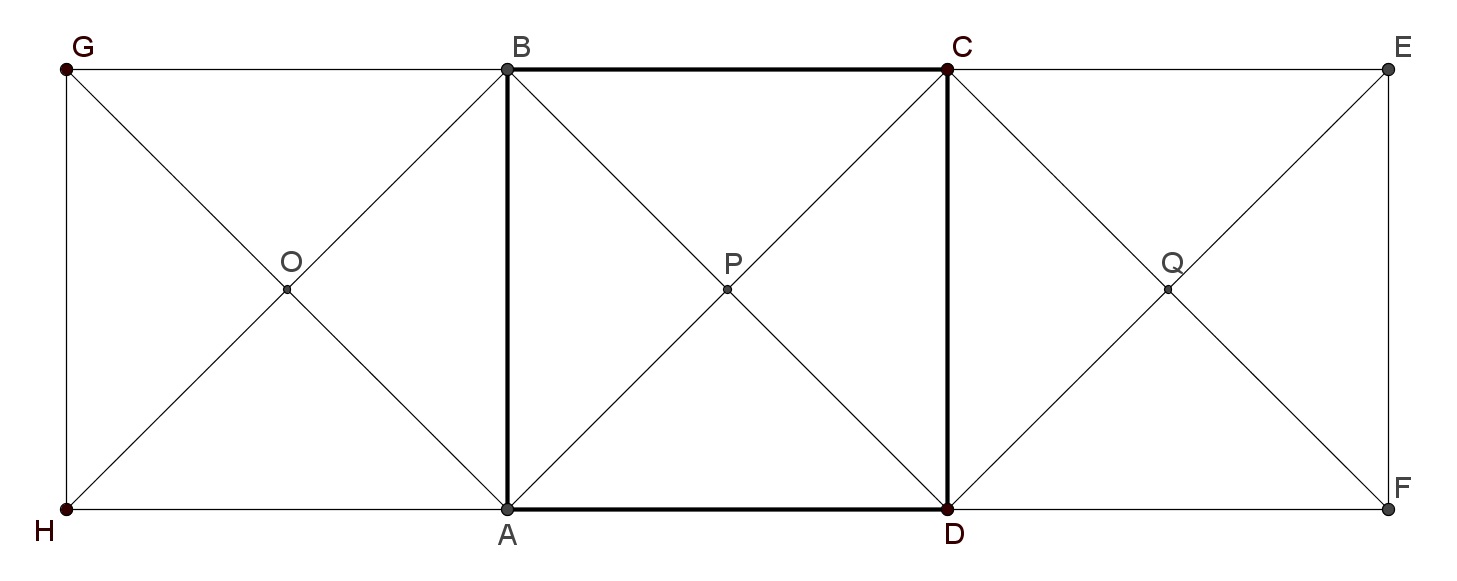
- \({\displaystyle R_{A,\frac{\pi}{2}} \circ R_{B,\frac{\pi}{2}}}\)
- \({\displaystyle R_{A,\frac{\pi}{2}} \circ T_{\stackrel{\longrightarrow}{CA}}}\)
- \({\displaystyle T_{\stackrel{\longrightarrow}{BC}} \circ T_{\stackrel{\longrightarrow}{AD}}}\)
- \({\displaystyle T_{\stackrel{\longrightarrow}{AB}} \circ R_{A,\frac{\pi}{3}}}\)
- \({\displaystyle T_{\stackrel{\longrightarrow}{AB}} \circ g_{\stackrel{\longrightarrow}{DC}}}\)
- \({\displaystyle r_{AD} \circ R_{C,\frac{\pi}{2}}}\)
- \({\displaystyle g_{\stackrel{\longrightarrow}{AC}} \circ g_{\stackrel{\longrightarrow}{BD}}}\)
- \({\displaystyle r_{AD} \circ T_{\stackrel{\longrightarrow}{AB}}}\)
Perform the following two transformations on the graph below with each square representing 1 square unit. After each transformation, draw the resulting image of segment \(\overline{PQ}\).
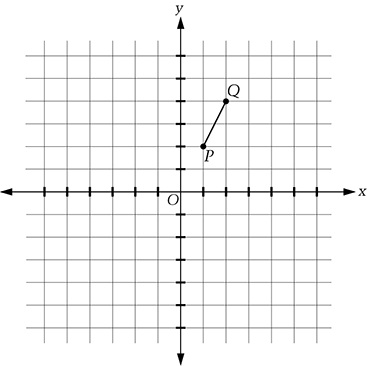
- Rotate the segment \(90^\circ\) counterclockwise about point \(P\) . Label the resulting segment \(I\). Find an algebraic representation of this rotation using a function of the complex plane and label this function \(f\).
- Reflect the segment \(I\) you drew in the first part across the \(x\) -axis. Label the resulting segment \(II\). Find an algebraic representation of this reflection using a function of the complex plane and label this function \(g\).
- Find an algebraic representation of the composition of the two transformations using a function of the complex plane and label this function \(h\).
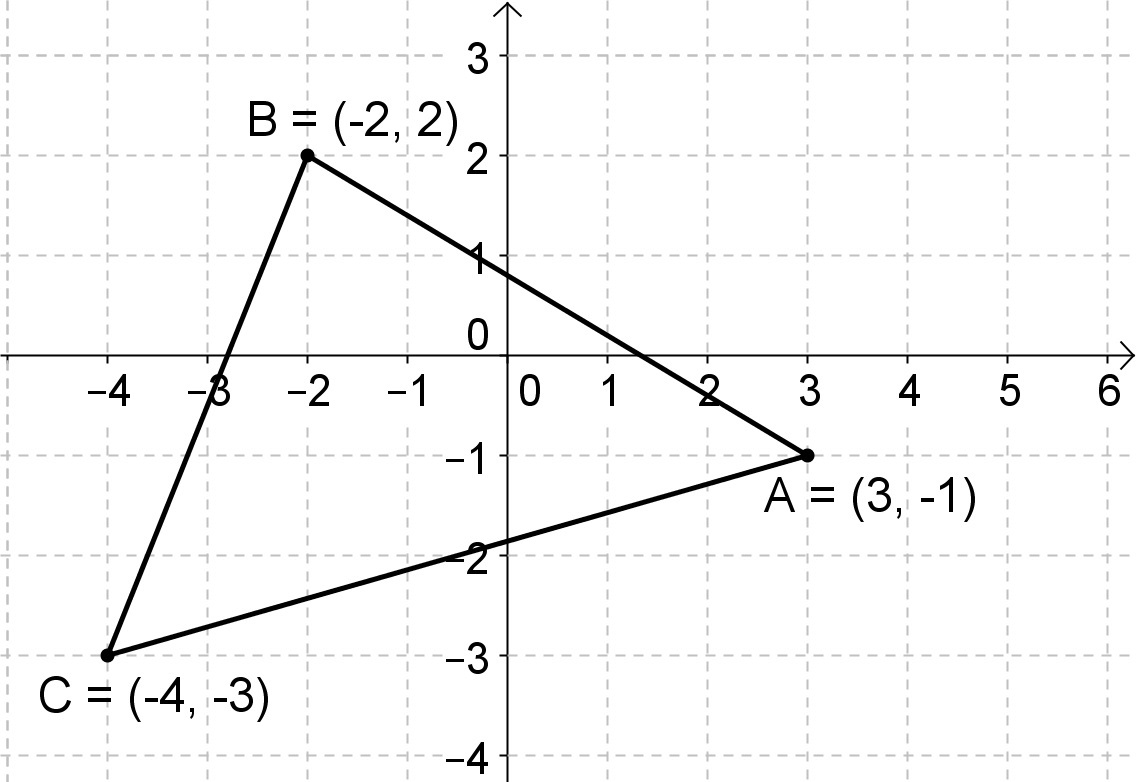
What are the coordinates of the image of \(\triangle ABC\) after a reflection across the \(y\)-axis followed by a rotation of \(90^\circ\) clockwise about the origin? Show your work, including a graph of the image of the triangle after each transformation, and explain how you found your answer.
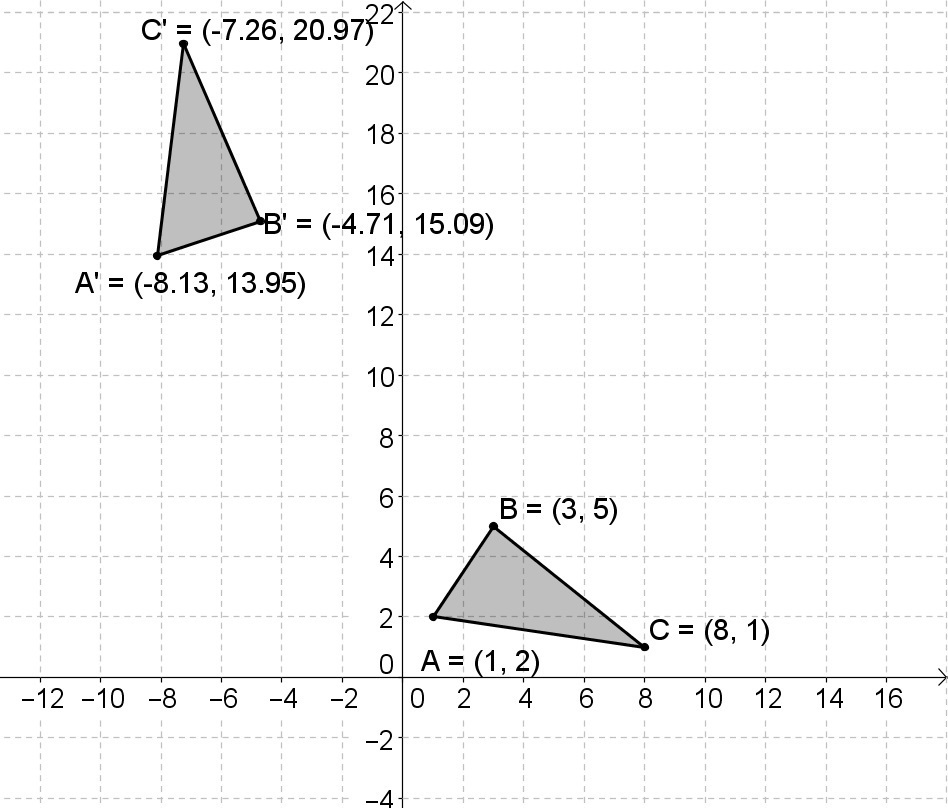
Find an algebraic representation of the rigid motion that takes \(\triangle ABC\) onto \(\triangle A'B'C'\). Explain your method for finding the transformation and why that method would work.
Let \(I\) be the set of isometries of the plane, i.e. \[I= \left\{ f:\mathbb{C} \rightarrow \mathbb{C} | f(z)=az+b \: \mbox{or} \: f(z)=a\overline{z}+b \mbox{ with } |a|=1 \right\}.\]
Let \(g\in I\), and \(\phi_g : I \rightarrow I\) be the function defined by \[\phi_g (f) = g^{-1} f g.\]
Prove that \(\phi_g\)
- maps the identity function to itself
- is one-to-one
- is onto
- maps translations to translations
- maps rotations to rotations
- maps reflections to reflections
Find all fixed points, if any, of the following plane transformations:
- The rotation \(R_{C,\theta}\)
- The translation \(T_b\) by the vector \(b\)
- The reflection \(r_m\)
For the given orientation preserving isometries, find two lines of reflection that will produce the described transformation. Express lines in the form \(y=mx+b\) or \(x=a\). Indicate the order they should be completed in.
- A rotation of \(\frac{\pi}{3}\) radians in the counterclockwise direction around the point \((0,0)\).
- A rotation of \(\pi\) radians in the clockwise direction around the point \((1,2)\).
- A translation equivalent to the vector \(\langle 3,4\rangle\).