1.3 Mathematical Practice Standards
Just like almost all of the content taught in secondary schools, the development of procedural habits and pieces of information are important parts of a secondary education, the heart of learning lies in developing habits of thinking, perseverance techniques, and developing communication skills to improve the ability to interact with the world around them. For example, the United Nations Educational, Scientific, and Cultural Organization (UNESCO) and the United Nations Office on Drugs and Crime (UNODC) (2019) described cognitive learning outcomes for secondary education such that a student “Knows about local, national, and global governance and accountability systems and structures, understands issues affecting interaction and connectedness of communities at local, national and global levels, (and) develops skills for critical inquiry and analysis” (p. 16). Mathematics, despite it’s reputation, aligns well with these goals. Critical thinking, reasoning, and communicating are the most important components of the secondary mathematics curriculum, and are often the most ignored.
The National Council of Teachers of Mathematics (2000) describes these goals in the -Principles and Standards for School Mathematics-, giving them the name ‘Process Standards.’ The National Governors Association Center for Best Practices and the Council of Chief State School Officers (NGA-CCSSO, 2010) expanded upon these to create the ‘Common Core State Standards Standards for Mathematical Practice.’ These practice standards are listed in Table 1.1 and more details about these standards can be found in their corresponding publications.
| Standards for Mathematical Practice | Process Standards |
|---|---|
| Make sense of problems and persevere in solving them. | Problem Solving |
| Reason abstractly and quantitatively. | Reasoning and Proof |
| Construct viable arguments and critique the reasoning of others. | Communication |
| Model with mathematics. | Connections |
| Use appropriate tools strategically. | Representations |
| Attend to precision | |
| Look for and make use of structure. | |
| Look for and express regularity in repeated reasoning. |
It is worth noting that these practices are expected of students of mathematics at all grade levels. In order to help others develop these practices, we must first develop them in ourselves. Only then will we be in a position to create a learning environment that motivates and enables students to grow in these practices.
To support the users of this text in developing these practices, opportunities to apply them are woven into the text, exercises, and projects. However, as any good teacher knows, the learner needs to be actively engaged in order for an objective to be reached. As you work through the text, pay attention to how the arguments are presented and seek to understand the process behind the mathematical content, rather than just procedures. When completing the exercises and projects, do not just try to get an answer. Instead, take some time to grapple with the ideas, think of better ways to communicate what you do not understand, and seek to understand the deeper connections involved in the task.
For the purpose of this text, we group these practice standards into four categories: mathematical problem solving, modeling with mathematics, communicating mathematically, and understanding mathematical structures. We briefly elaborate on each in the following sections.
1.3.1 Mathematical Problem Solving
Mathematical problem solving is perhaps the most widely cited application of mathematics “in the real world”. Although generally acknowledge as important, problem solving is a complex process that is difficult to teach. In his book, How to Solve It: A new aspect of mathematical method, George Pólya described four phases of the problem solving process (See Figure 1.2 when approaching mathematical problems (Polya, 1957). While many others have expanded on this problem solving process, much of the thinking around problem solving still traces back to the four phases that Pólya describes.
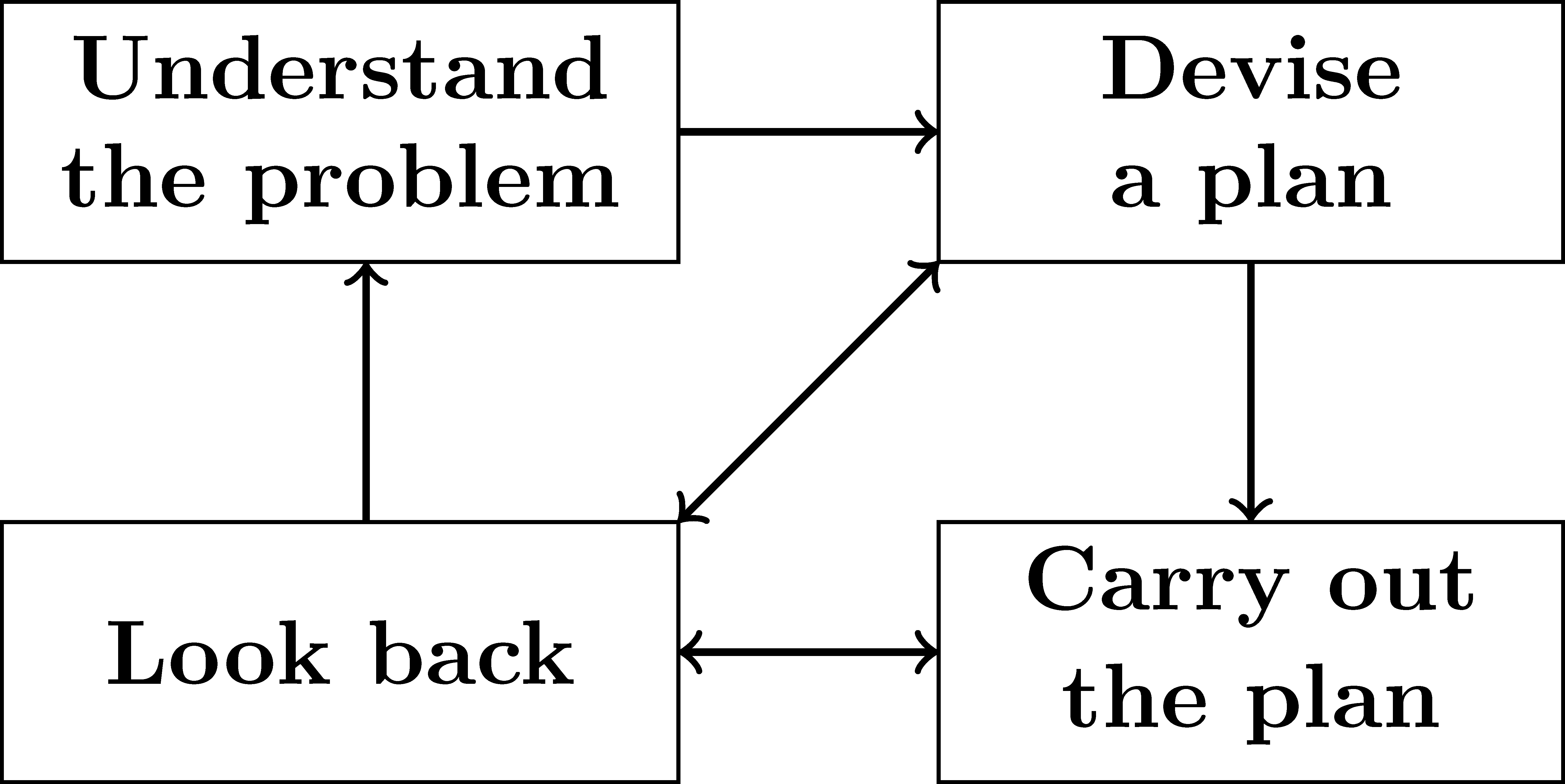
Figure 1.2: Pólya’s problem solving process
The first phase is the process of understanding the problem. What this phase looks like varies by problem, but often involves making sure you understand what information is given and relevant. It also includes knowledge of what an answer should look like for the question posed and, where relevant, being able to organize the provided information in a picture or diagram to better understand the situation. So, for example, if the problem is computational, understanding the problem may entail understanding whether positive or negative answers are valid solutions. If the problem is a theorem that needs proving, this phase may involve generating related examples or writing out relevant definitions to make sure you understand the given inputs and implications of the theorem.
The second phase of the problem solving process is to devise a plan. Many students struggle in the problem solving process because they only want to solve problems for which they have previously been given a template. The origin of this desire has roots in the fact that many teachers only assign students problems that are similar to those discussed in class. True mathematical problem solving involves confronting problems for which the solution is not immediately obvious to the problem solver. In problem solving, one may need to connect the current problem to previously solved problems or restate the problem in a different form with an easier solution process. Sometimes a full plan is not possible at the beginning and the solver needs to just plan initial steps and work through those to gather more information about the problem that will help them create a new plan later in the process.
Once an initial plan is devised, it needs to be carried out. This is often the simplest part of the problem solving process, and often the only component that students complete. With today’s technology, computer applications can often complete the details of this part of the problem solving process through statistical analyses, computer algebra systems, or graphical programs. While there are benefits of technology, it is important that the students understand the process.
After the plan is carried out, it is important to look back, completing the final phase of the problem solving process. In this step the problem solver determines whether their solution makes sense in the context of the original problem. For example, in calculus, it is often possible to obtain negative solutions that are not appropriate to the problem posed. The final step of looking back also entails making sure that we have actually addressed the question asked or the problem posed, rather than a different, somewhat related, question or problem.
Although these four phases appear linear, the majority of mathematical problems require various iterations of these phases. In particular, it is often the case that the first plan created to solve a problem does not work, so it has to be revised following an attempt to carry it out. Good problem solvers see these revisions as opportunities to learn more about the problem, rather than as failure at the problem solving process.
1.3.2 Modeling with Mathematics
Mathematical problem solving often relies on modeling with mathematics, particularly in the context of real-world phenomena. The Guidelines for Assessment and Instruction in Mathematical Modeling Education (GAIMME) defines mathematical modeling as “a process that uses mathematics to represent, analyze, make predictions or otherwise provide insight into real-world phenomena” (GAIMME, 2019, p. 8). This definition varies from other common connotations of “modeling” that are used in education, including in mathematics. For example in mathematics education, using manipulatives to model a mathematical idea; sketching graphs or pictures to communicate or understand concepts; and demonstrating how to solve certain types of problems are all referred to as modeling. However, as a process standard, modeling mathematics does not generally include these activities. Instead, it refers to activities of using mathematics to analyze, predict, and represent real-world data.
The GAIMME Report breaks the mathematical modeling process into the six components shown in Figure 1.3. Critically, these six components do not happen in a progression, but instead are iterative and sometimes run parallel to each other.
![The Math Modeling Process [@GAIMME, p. 13]](tikz/GAIMME.png)
Figure 1.3: The Math Modeling Process (GAIMME, 2019, p. 13)
The focus on trying to better understand real-world phenomena distinguishes mathematical modeling from application problems or word problems. Actual real-world phenomena are distinctly messy and arriving at a final solution requires interpretation and assumptions. Moreover, an individual engaged in modeling has to confront the challenge of determining whether the question, mathematical model, and data are well-aligned. Teachers face the additional challenge of ensuring that the situations they create for their students are appropriate for their students. For instance, an elementary school classroom might plant some seeds in the soil. The teacher would then assist the students in identifying specific questions that can be answered quantitatively about the seeds and plants, guiding them towards a set of questions and data that the children could collect, analyze, and interpret. A secondary teacher teaching about exponential functions may introduce the class to the concept of population growth and guide the students to questions that can be answered quantitatively with exponential models. In both these examples, the instructor introduces the students to a real-world situation and then guides them to questions that facilitate the students’ development of the mathematical modeling they want to discuss.
Another key aspect of the modeling process involves determining the relevance of various quantities in the situation and how to describe them with variables. This cyclical process involves identifying variables, assigning them labels and then assessing how they fit in with other variables. This process allows the modeler to create an idealized version of the original problem in order to create some type of solution. It is important during the process to justify each assumption made and to clearly label each variable, along with its appropriate units. It is through this justification process that the modeler can communicate the applicability and interpretation of the results from the model to the consumer.
As the modeler defines the variables and the relationships between them, they can use the mathematical problem solving techniques to ‘do the math’ and come up with possible solutions to the problems posed. This section of ‘doing the math’ reflects the word problems of most math textbooks since the word problems rarely have extraneous information and have obvious variables defined with transparent relationships between them.
Similar to the ‘looking back’ phase of the mathematical problem solving process, the modeling process includes a stage during which the modeler steps back and assesses the model. During this stage he or she analyzes and tests the model and solution, examining the model created and determining the appropriateness and accuracy of the solution produced. This process often results in a revision to the original assumptions and adjustments to the model with improved variables and relationships between the variables.
Since the mathematical modeling process deals with messy real-world phenomena, an iterative process of reflection that results in the refinement and, where appropriate, extension of the the model is a key component that almost always appears in a modeling cycle. This process may run parallel to or between any of the other phases of the modeling process.
When the model gets to a state that satisfies the modeler in terms of the model justifications and appropriateness of the solutions, the implementation of the model and the reporting of the results occurs. The presentation of the results must include the justification for the model, a description of the various assumptions made to produce the model, and any limitations the model has in terms of the accuracy of the results. This presentation must be done in a way that is comprehensible to the desired audience. Because modeling deals with real-world situations, the solution is unlikely to be clear or definitive, but will instead be approximate and estimated.
1.3.3 Communicating Mathematically
Mathematical communication broadly relates to the ways and methods of representing, justifying, and interpreting mathematics. More specifically, the practice of mathematical communication “encompasses both listening and reading (comprehension) and both speaking and writing (expression)… and may also include representation of mathematical ideas in nonlinguistic ways” (Sammons, 2018, p. 7). In order to better understand the practice of communicating mathematically, we examine six overlapping concepts that are at the core of this practice (see Figure 1.4).

Figure 1.4: Components of Mathematical Communication
All types of communication require a language. Within a language there exists a shared meaning behind the words and symbols used when communicating with a particular language. Mathematics communication, in this sense, operates much as a language does. However, unlike a language such as English, mathematics is represented using a mixture of words that have very precise definitions and symbols that compress many different ideas and meanings into a very small amount of space (linguists call mathematics a “dense” language because of this property). For example, the sentence \[\left\{ f: \mathbb{C}\rightarrow \mathbb{C} \vert f(z)=az+b, \: a,b\in \mathbb{C}\right\}\] is very concise in terms of symbols, but contains a large amount of mathematical language and concepts that the average person may not understand.
Moreover, somewhat uniquely to mathematics, the meaning of symbols varies widely depending upon the context of the communication. Consider variables, which are usually represented using any number of symbols. While certain types of symbols will cue a well-informed mathematics student that a variable has some implied meaning in terms of what type of number system to which it belongs, even in this case variables in different circumstances serve different roles. Sometimes the letter represents a fixed value (e.g., \(x=4\)) and other times it represents a range of values that satisfy a particular condition (e.g., \(x\leq 4\)). Sometimes it indexes a set, while other times it represents a function. The differences between these uses are often subtle, making explicit training in these nuances mathematics critical.
Once the language of mathematics has been developed, the grammar is created. In mathematics, logic, argument, and proof form the core patterns of organization and presentation. Together, logic, argument, and proof boil down to the ability to construct viable arguments and critique the arguments of others using mathematical evidence.
Part of mathematical communication is learning how to consume and understand the ideas of others. In mathematics this usually occurs by reading or listening to the arguments of others. Both reading and listening to mathematics require a great deal of practice and are skills students must hone over many courses. In particular, reading mathematics requires a great deal of practice and discipline. While a novel can usually be consumed at a steady pace without much explicit effort by the reader, written mathematical ideas are often presented symbolically, with the reader left to fill in certain logical steps. Thus, the act of reading mathematics becomes one of translation of the symbolic work into a language he or she understands, followed by a effort to connect current parts of the argument to previously made points, and the absorption and evaluation of those ideas based on previous knowledge. As a result, reading mathematical texts and arguments requires a big investment in time. Sometimes it can take hours just to understand one line of a mathematical text! This slow, methodical way of reading is challenging to students of mathematics, but is a critical skill to develop as it is core to the practice of doing mathematics.
Previous paragraphs have described the difficulties and process of consuming mathematical texts. However, it is also important that students learn to produce their own mathematical communications in both oral and written forms. In communicating to others, it is essential that precise mathematical words are used, rather than slang, in order to reduce the confusion of potential readers. It is also useful to employ a variety of mathematical representations, including graphs, sketches, and diagrams to facilitate the communication of mathematical ideas.
As teachers of mathematics, we must continually emphasize the development of this practice of communicating mathematically by de-emphasizing simple answers to mathematical problems, teaching students how to read and write mathematics (not just about mathematics), and to promote classroom discourse to provide opportunities for students to experience different types of mathematical communication.
1.3.4 Understanding Mathematical Structures
While the definition of mathematics is not uniform or agreed on, most agree that mathematics is inherently about the study of underlying structures and logical reasoning. For example, the Encyclopædia Britannica -Fraser et al. (2019) defines mathematics as “the science of structure, order, and relation that has evolved from elemental practices of counting, measuring, and describing the shapes of objects.” This means that an important practice in the doing of mathematics is to “look for and make use of structure” and to “look for and express regularity in repeated reasoning” (NGA-CCSSO, 2010).
The pursuit and use of structure and regularity appear throughout all of mathematics. Mathematical structure informs every part of mathematics teaching, from instruction on common mathematical procedures to searching for and making connections between various, apparently unrelated, mathematical content areas to provide new insight into a problem. As teachers, we need to point out these mathematical structures to the students and help them learn how to discover the structures and regularity on their own.
1.3.5 Exercises
Consider the following mathematical task:
An electricity company charges Kelly \(\$0.15\) per kWh (kilowatt-hour) of electricity used, plus a basic connection charge of \(\$8.00\) per month. Find a function that helps Kelly estimate her monthly electricity bill for a given number of kWhs. Be explicit about the domain of the function you create.
NCTM emphasizes multiple representation of functions using verbal, tabular, graphical, and symbolic representations. Using this word problem as the verbal representation, express the function in each of the remaining ways.
How does the ability to move between different representations of functions support students’ development of the mathematical communication process standard?
The problem solving section discussed the fact that a mathematical task is only considered a problem if the person working on the task does not know in advance a solution method that will produce a correct answer. Would you say that for part (a) you were engaged in mathematical problem solving as described in the standards? Why or why not?
Under what conditions would the task be a problem for students you were teaching?
Based on the description of mathematical modeling, would you say that finding the function for the task in part (a) represents mathematical modeling? Why or why not?
A second part of the task asks students to estimate Kelly’s electrical bill for the year, given that her monthly kWh usage ranges between 202 and 254 kWh.
The textbook you got the problem from lists the answer to the extension as \(\$506.40\). What did the author do and what assumptions did she make in order to arrive at that answer? Do you agree with her process and assumptions? Why or why not?
In arriving at your answer for part (a), would you say that you were engaged in mathematical problem solving? Why or why not?
If you were using this task as a modeling activity for your students, what criteria would you use to evaluate whether their answer was reasonable?
There are five NCTM Process Standards and eight Common Core Standards for Mathematical Practice. While there is significant overlap between the two sets of standards, they are not the same. Read each set of standards. When there is overlap between the two sets of standards, create a map between them. Also identify the ways in which the two sets of standards differ. These regions are not at the heading level. You’ll have to actually dig into the blurbs about each standard in their original documents.
A basic theorem that students use from an early age is that the sum of two even integers is even. A typical proof of this theorem might look something like this:
Let \(a\) and \(b\) be even integers such that \(a=2m\) and \(b=2n\) where \(m\) and \(n\) are integers. Then \(a+b=2m+2n=2(m+n)\). Thus, the sum of two even integers is even.
The section on mathematical communication emphasizes the reliance of mathematical communication on precise definitions and symbols that compress complex ideas into short phrases. In examining this proof, identify the places where the problem statement or proof rely on a definition or compressed expression.
Identify the places where the proof writer has left the reader to fill in logical steps or rationales.
Rewrite the proof of the theorem without the use of any symbols, but with the same degree of precision and generalizability.
In comparing the symbolic proof to your verbal proof, do you think it is easier to understand (i.e., more like a novel?) or do you think it would still be difficult to read if all mathematics were presented without symbols? Why or why not?
If you reflect on the six parts of mathematical communication, which parts do you think you are best at? Which parts do you struggle the most with? What is one goal you have for yourself for mathematical communication that you want to develop during this course?