10.6 Centers of Triangles

When we think about a “center” of a triangle, there are many different properties that we may want. We will now explore how some of these properties generate various “centers” of a triangle.

10.6.1 Centroid

The first “center” that we will consider is the point that is the arithmetic mean of all of the points contained inside of the triangle. From a physics perspective, this point is the center of mass, or the balance point, for the triangle. To generate this point, we need to first create some definitions.

Definition 10.7 The median of a side of a triangle is the segment connecting the midpoint of the side to the opposite vertex.

So for \(\triangle ABC\), if \(D\) is the midpoint of \(AB\), then \(CD\) is the median of \(AB\).

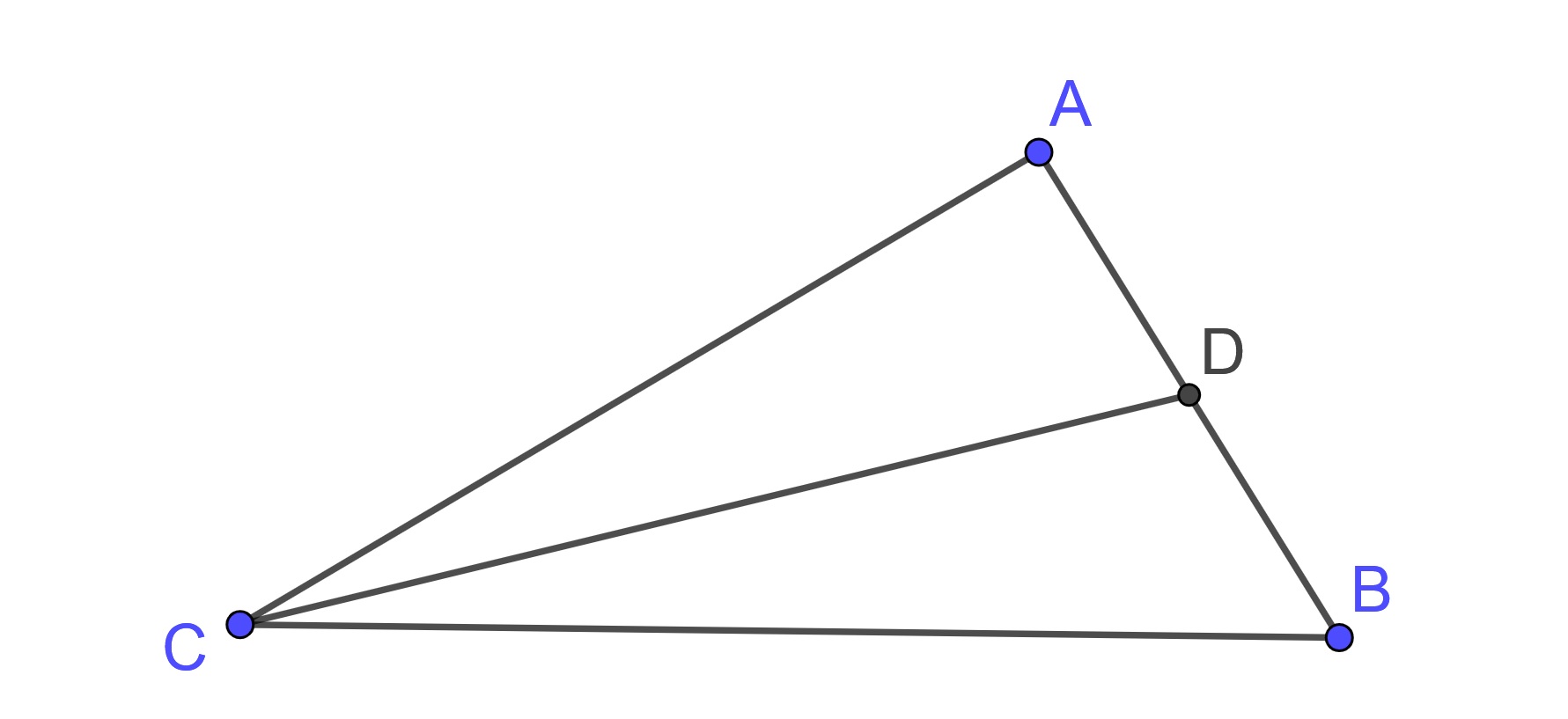
Theorem 10.17 Medians of a triangle are concurrent at a point.

We will give an outline of the proof in a series of lemmas with some key details left to be filled in. We recommend that as you read through the proof you should use a dynamic geometry application to construct the diagrams and to study properties of the constructions.

Lemma 10.1 Let \(\triangle ABC\) be given. Let \(A'\) be the midpoint of \(BC\), \(B'\) be the midpoint of \(AC\), and \(C'\) be the midpoint of \(AB\).

Then \(\triangle A'B'C\sim \triangle BAC\) with \[\frac{A'B'}{BA}= \frac{A'C}{BC} = \frac{B'C}{AC}=2\] and triangles \(\triangle AB'C'\), \(\triangle B'A'C\), \(\triangle C'BA'\), and \(\triangle A'B'C'\) are all congruent and so are also all similar to \(\triangle ABC\) with ratio of \(1:2\).

Proof. Let \(\triangle ABC\) be given. Let \(A'\) be the midpoint of \(BC\), \(B'\) be the midpoint of \(AC\), and \(C'\) be the midpoint of \(AB\).

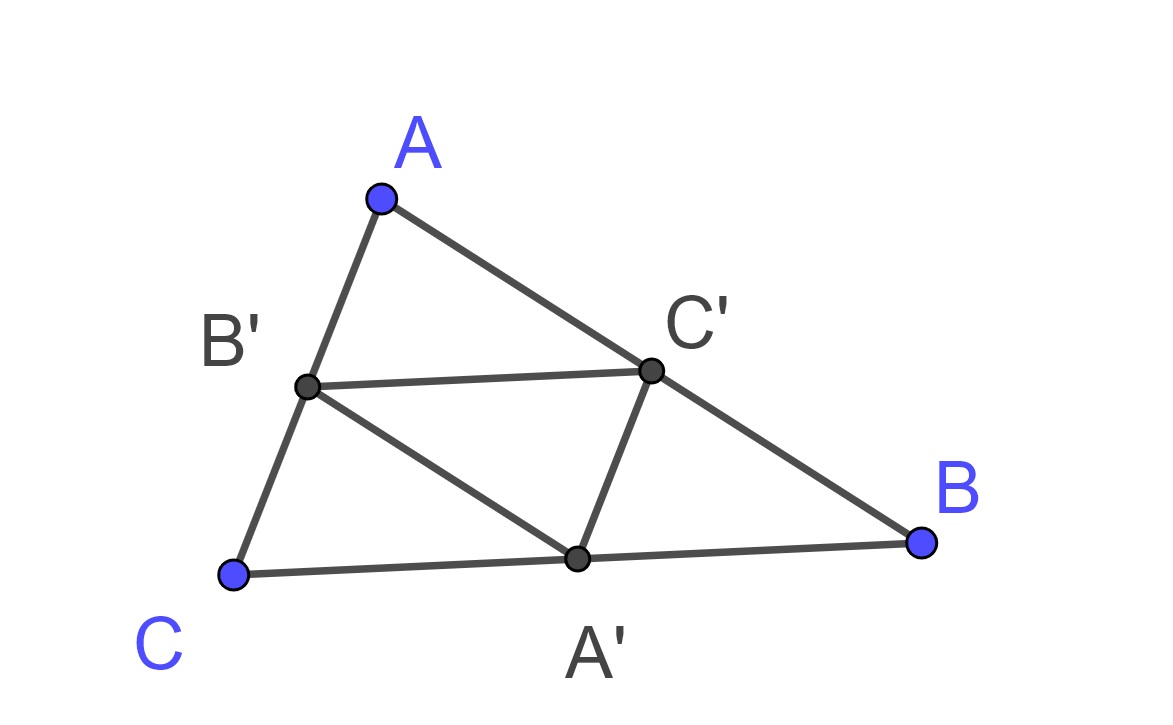
Since \(A'\) is the midpoint of \(BC\), \(B'\) is the midpoint of \(AC\), and angles \(\angle BCA\) and \(\angle A'CB'\) are equal, by Theorem 10.16 we know that \(\triangle A'B'C\sim \triangle BAC\) with \[\frac{A'B'}{BA}= \frac{A'C}{BC} = \frac{B'C}{AC}=\frac{1}{2}.\]

Using similar arguments, we have that \(\triangle AB'C' \sim \triangle ACB\) and \(\triangle BC'A' \sim \triangle BAC\) with a ratio of \(1:2\).

We now know that \[\frac{A'B'}{AB}=\frac{A'C'}{AC} = \frac{B'C'}{BC} = \frac{1}{2}\] and so by Theorem 10.15 \(\triangle A'B'C' \sim \triangle ABC\) with a ratio of \(1:2\).

So the segments connecting the midpoints of the sides of a triangle create four congruent triangles that are similar to the original triangle and whose side lengths are half the length of the original.

Related Content Standards

• (HSG.CO.10) Prove theorems about triangles. Theorems include: measures of interior angles of a triangle sum to \(180^\circ\); base angles of isosceles triangles are congruent; the segment joining midpoints of two sides of a triangle is parallel to the third side and half the length; the medians of a triangle meet at a point.

Lemma 10.2 The segments joining the midpoints of two sides of a triangle is parallel to the third side and half the length.

Proof. The proof the previous lemma included that the segments joining the midpoints of two sides of a triangle is half the length of the third side. So we only need to prove that it is parallel to the third side.

Since the four triangles inside of the original triangle are congruent to one another we know that the angles \(\angle BC'A'\) and \(\angle B'A'C'\) are equal. Since these are alternate interior angles of the transversal \(A'C'\) crossing \(AB\) and \(A'B'\) we see that \(A'B'\) is parallel to \(AB\). We use the same argument to show that the other two segments are parallel to the corresponding sides of the triangle.

Lemma 10.3 Let \(\triangle ABC\) be given. Let \(A'\) be the midpoint of \(BC\), \(B'\) be the midpoint of \(AC\), and \(C'\) be the midpoint of \(AB\) and let \(G\) be the point of intersection of \(AA'\) and \(BB'\).

Then \(\triangle AGB \sim \triangle A'GB'\) and \[\frac{AG}{A'G} = \frac{BG}{B'G} = \frac{AB}{A'B'} = 2.\]

Proof. Let \(\triangle ABC\) be given. Let \(A'\) be the midpoint of \(BC\), \(B'\) be the midpoint of \(AC\), and \(C'\) be the midpoint of \(AB\) and let \(G\) be the point of intersection of \(AA'\) and \(BB'\).

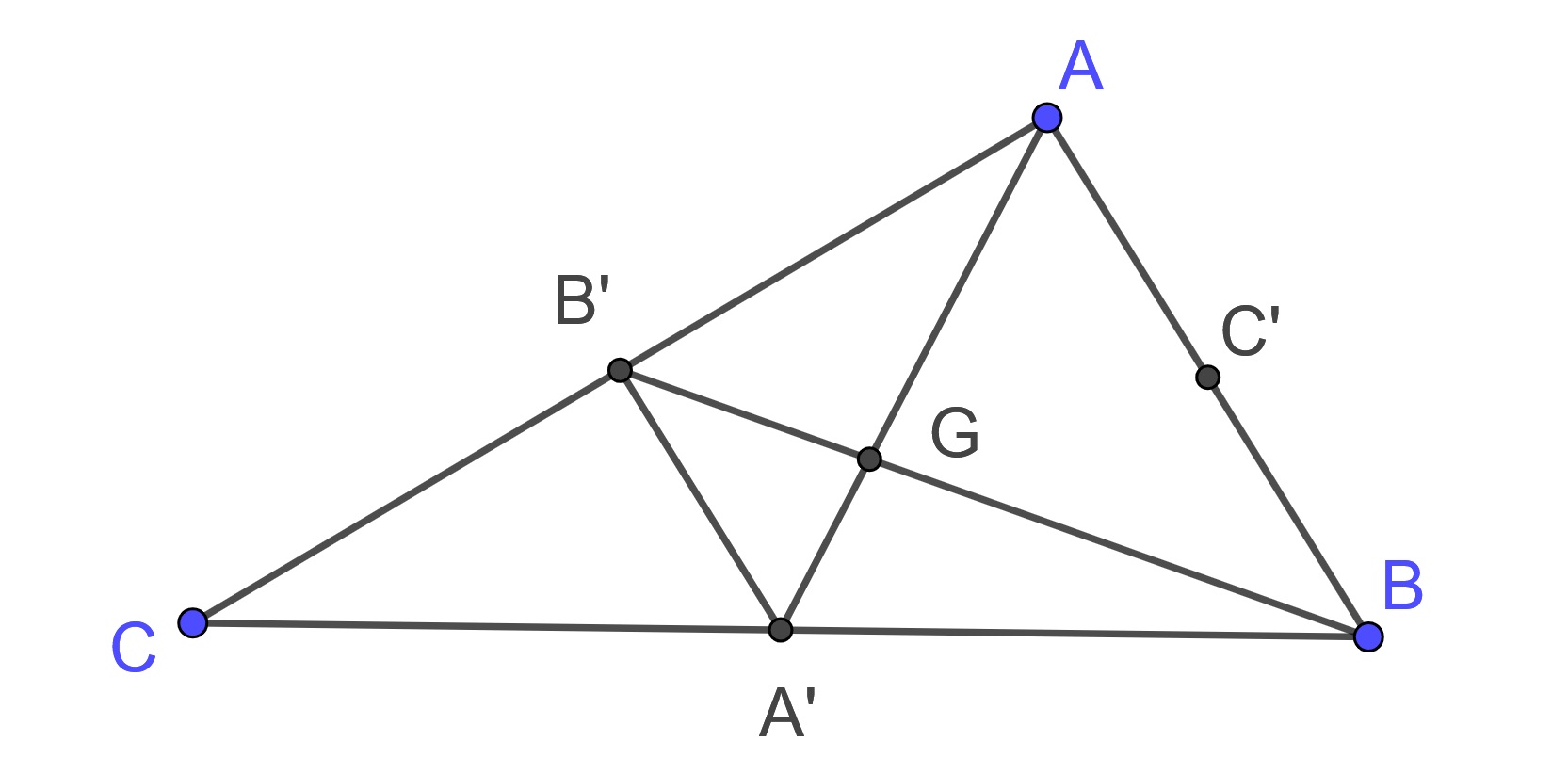
Since \(AB\) is parallel to \(A'B'\) we know that \(\angle GA'B' = \angle GAB\) and \(\angle GB'A' = \angle GBA\) since they are alternate interior angles. Also, \(\angle A'GB' = \angle AGB\) because they are vertical angles. So \(\triangle AGB \sim \triangle A'GB'\) by the definition of similarity. Since \[\frac{AB}{A'B'} = 2\] we have the remainder of the ratios by Theorem 10.15.

We can use the same arguments to prove the following lemma about the intersection point of \(AA'\) and \(CC'\).

Lemma 10.4 Let \(\triangle ABC\) be given. Let \(A'\) be the midpoint of \(BC\), \(B'\) be the midpoint of \(AC\), and \(C'\) be the midpoint of \(AB\) and let \(G'\) be the point of intersection of \(AA'\) and \(CC'\).

Then \(\triangle AG'C \sim \triangle A'G'C'\) and \[\frac{AG'}{A'G'} = \frac{CG'}{C'G'} = \frac{AC}{A'C'} = 2.\]

Question: Why do we give the point of intersection of \(AA'\) and \(CC'\) a separate name rather than just calling it \(G\)?

Since \(G\) and \(G'\) are both on \(AA'\) and \(\frac{AG}{A'G} = \frac{AG'}{A'G'} = 2\) we see that \(G=G'\).

Question: Why is proving that \(G\) and \(G'\) are at the same point along a median segment sufficient for proving that \(G=G'\)? Be as specific as possible.

So the medians \(AA'\), \(BB'\), and \(CC'\) are concurrent.

Definition 10.8 The centroid of a triangle is the point of concurrence of the medians of the sides of the triangle.

10.6.2 Circumcenter

The next “center” we consider is the point whose distance is the same from the three vertices of the triangle and so is the center of the circle that circumscribes the triangle. A unique property of this point is that it is not always inside of the triangle. One can prove that the circumcenter is inside of the triangle if and only if the triangle is acute.

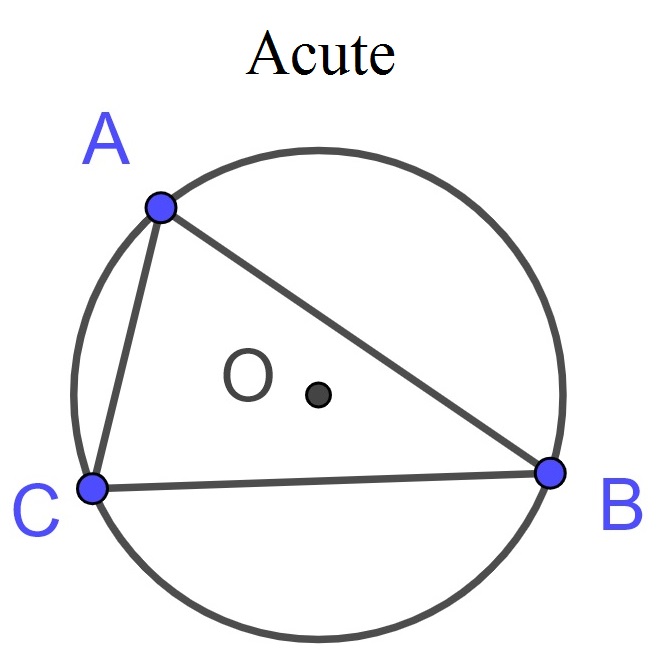
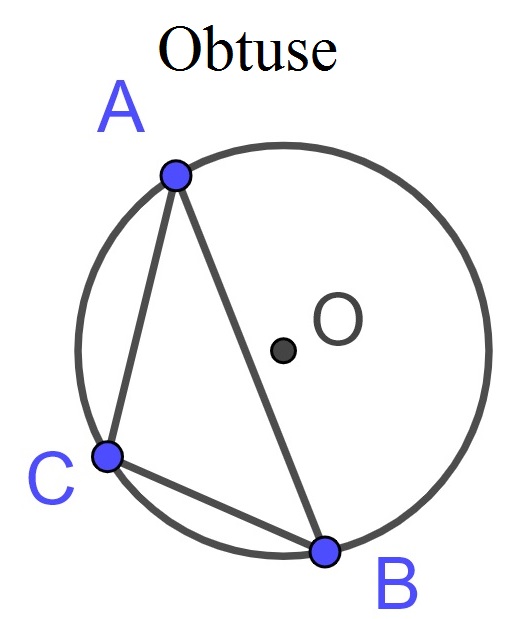
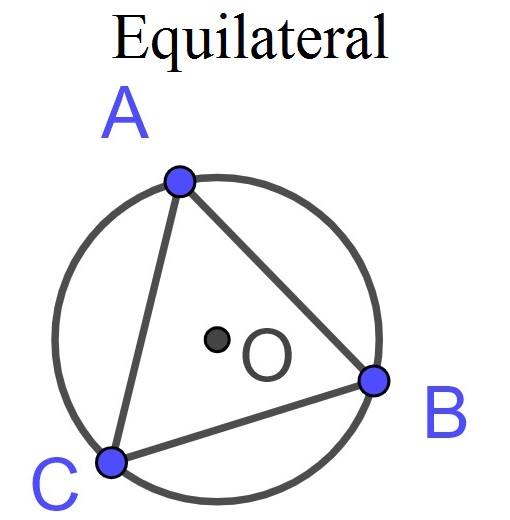
Figure 10.5: Sample Venn diagrams

Theorem 10.18 The perpendicular bisectors of the three edges of a triangle are concurrent at a point.

Proof. Let \(\triangle ABC\) be given and let \(O\) be the point of intersection of the perpendicular bisectors of \(AB\) and \(AC\). Because \(O\) is on the perpendicular bisector of \(AB\), \(AO=BO\). Since \(O\) is on the perpendicular bisector of \(AC\), \(AO=CO\). By transitivity, \(BO=CO\) and so \(O\) is on the perpendicular bisector of \(BC\). So the perpendicular bisectors are concurrent.

Definition 10.9 The circumcenter of a triangle is the point of concurrence of the perpendicular bisectors of the sides of the triangle.

10.6.3 Orthocenter

A third point related to the triangle involves the point of intersection of the altitudes of the triangle.

Definition 10.10 The altitude of a vertex of a triangle is the segment connecting the vertex of a triangle to a point on the extension of the opposite side of the triangle so that the segment is perpendicular to the opposite side.

In each of the two triangles below, \(AA'\) is the altitude of \(A\). In the first triangle, the altitude is outside of the triangle, while it is inside of the triangle in the second example.

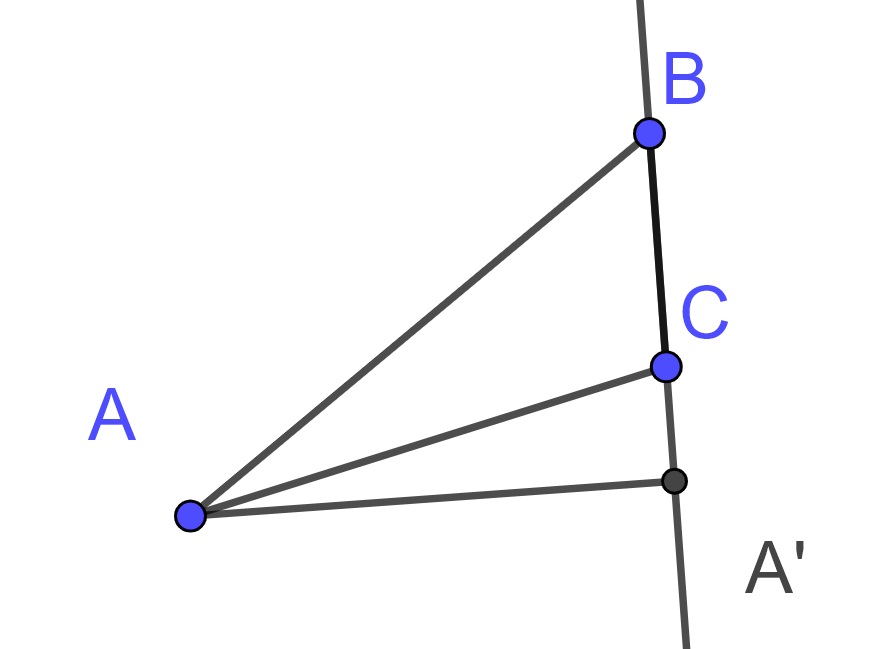
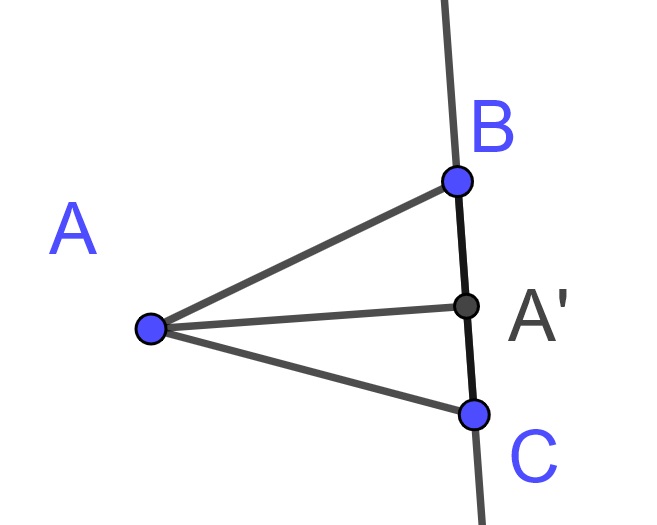
In order to prove that the altitudes are concurrent we will first prove a useful theorem regarding concurrency proved by Giovanni Ceva (1648-1734).

Theorem 10.19 (Ceva's Theorem) In a triangle \(\triangle ABC\), three lines \(AD\), \(BE\), and \(CF\) intersect at a single point \(K\) if and only if \[\frac{AF}{FB} \cdot \frac{BD}{DC} \cdot \frac{CE}{EA} = 1.\]

Proof. We first assume that the three lines \(AD\), \(BE\), and \(CF\) are concurrent. We can then extend the lines \(BE\) and \(CF\) beyond the triangle until they meet \(GH\), the line through \(A\) parallel to \(BC\).

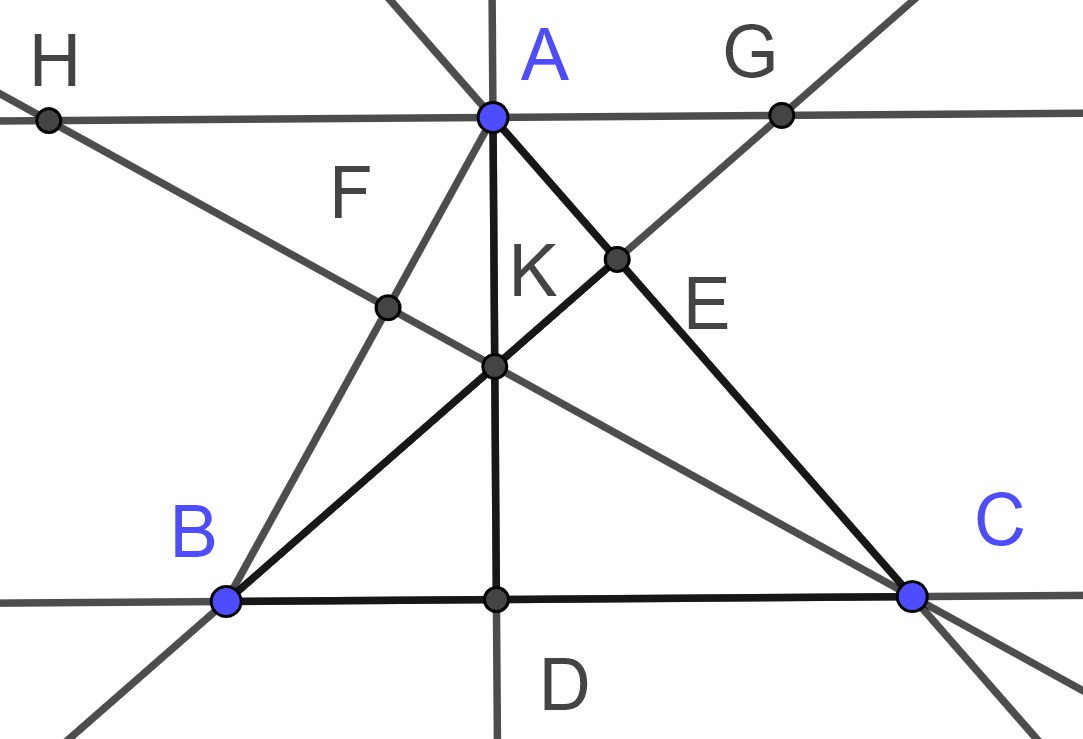
By alternate interior angles, \(\angle AHF\) and \(\angle BCF\) is equal and by vertical angles, \(\angle AFH\) and \(\angle CFB\) are equal. So by Theorem 10.14, \(\triangle AHF \sim \triangle BCF\). Using the same type of arguments, \(\triangle AGE \sim \triangle CBE\).

We can also use similar arguments to show that \(\triangle AGK \sim \triangle BDK\) and \(\triangle CDK \sim \triangle AHK\).

These similar triangles imply the following proportions:

\[ \frac{AF}{FB} = \frac{AH}{BC}, \quad \frac{CE}{EA} = \frac{BC}{AG}, \quad \frac{AG}{BD} = \frac{AK}{DK}, \quad \frac{AH}{DC}=\frac{AK}{DK}\]

From the last two proportions we conclude that \(\frac{AG}{BD} = \frac{AH}{DC}\) and so \(\frac{BD}{DC} = \frac{AG}{AH}\).

Using these proportions we have that \[\frac{AF}{FB} \cdot \frac{BD}{DC} \cdot \frac{CE}{EA} = \frac{AH}{BC} \cdot \frac{AG}{AH} \cdot \frac{BC}{AG} = 1.\]

In order to prove the converse, we will assume \[\frac{AF}{FB} \cdot \frac{BD}{DC} \cdot \frac{CE}{EA} = 1\] and prove that this implies \(AD\), \(BE\), and \(CF\) are concurrent.

Assume that \(K\) is the point of intersection of \(BE\) and \(CF\) and draw the line \(AK\) until its intersection with \(BC\) at a point \(D'\). Then, from the just proven part of the theorem it follows that \[\frac{AF}{FB} \cdot \frac{BD'}{D'C} \cdot \frac{CE}{EA} = 1.\]

On the other hand, it’s given that \[\frac{AF}{FB} \cdot \frac{BD}{DC} \cdot \frac{CE}{EA} = 1,\] so that \(\frac{BD'}{D'C} = \frac{BD}{DC}\) implying that \(D\) and \(D'\) are the same point. So the segments are concurrent.

Theorem 10.20 The lines extending altitudes of the vertices of a triangle are concurrent.

Proof. Let \(\triangle ABC\) be given. Let \(A'\) be point on the line \(BC\) so that \(AA'\) is the altitude of \(A\), \(B'\) be the point on the line \(AC\) so that \(BB'\) is the altitude of \(B\), and \(C'\) be the point on the line \(AB\) so that \(CC'\) is the altitude of \(C\).

We have that triangles \(\triangle ACA'\) and \(\triangle BCB'\) are similar because they both have a right angle and share an angle at \(C\). So \(\frac{CB'}{A'C}=\frac{BB'}{AA'}\). Similarly, \[\frac{AC'}{B'A} = \frac{CC'}{BB'} \quad \mbox{ and } \quad \frac{BA'}{C'B}=\frac{AA'}{CC'}.\]

Therefore, \[\frac{AC'}{C'B} \cdot \frac{BA'}{A'C} \cdot \frac{CB'}{B'A} = 1\] and Ceva’s Theorem implies that the lines are concurrent.

Definition 10.11 The point of concurrency of the extensions of the altitudes of the vertices of a triangle is called the orthocenter.

10.6.4 Euler Line

Leonard Euler showed in 1765 that the centroid, circumcenter, and orthocenter of a triangle are colinear and the line through these three points is called the Euler line of the triangle.

Theorem 10.21 (Euler Line) Given a triangle \(\triangle ABC\) with centroid \(G\), circumcenter \(O\), and orthocenter \(H\), the points \(G\), \(H\), and \(O\) are colinear with \(G\) between \(O\) and \(H\) and is twice as far from the orthocenter as from the circumcenter, \(GH=2GO\).

10.6.5 Exercises

1. Reflection questions about the centroid.

   1. At what points in the proof, if any, were axioms or common definitions used to illuminate something?
   2. At what points in the proof, if any, were definitions used to illuminate something?
   3. When, if at all, were propositions or theorems used to illuminate something?
   4. How were theorems used in the proof? (i.e., focus on what work went into using the theorem).
   5. In geometry, students often struggle with the fact that a picture of the thing they are proving “shows” the result, so it seems pointless to write everything out. Why do you think we insist on doing it this way anyway?

2. Prove that the angle bisectors of a triangle are concurrent. This point of concurrency is called the incenter of the triangle.